Авторизация
Поиск по указателям
Jordan C. — Calculus of Finite Differences
Обсудите книгу на научном форуме Нашли опечатку?
Название: Calculus of Finite DifferencesАвтор: Jordan C. Аннотация: This book, a result of nineteen years’ lectures on the Calculus of Finite Differences, Probability, and Mathematical Statistics in the Budapest University of Technical and Economical Sciences, and based on the venerable works of Stirling, Euler and Boole, has been written especially for practical use, with the object of shortening and facilitating the labours of the Computer. With this aim in view, some of the old and neglected, though useful, methods have been utilized and further developed: as for instance Stirling’s methods of summation, Boole’s symbolical methods, and Laplace’s method of Generating Functions, which last is especially helpful for the resolution of equations of partial differences.
Язык: Рубрика: Математика /Анализ /Учебники по элементарному анализу /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: 2-nd editionГод издания: 1950Количество страниц: 652Добавлена в каталог: 09.04.2005Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
146 202 204 266 152 172 347 351 438 349 349 352 351 348 449 450 155 154 429 Addition of differences, method of 76 Alternate functions 92—94 Alternate functions, sum of 320 324 Alternate functions, summation by parts 108 Alternate reciprocal powers am numbers, table of 232 251 Alternate reciprocal powers, expressed by sums 251 Alternate reciprocal powers, generating function of 251 Alternate reciprocal powers, sum of 251 Antilogarithmic tables 399 402 Approximation by Bernoulli's probability function 432 Approximation by incomplete B function 428 Approximation by incomplete r function 426 Approximation by Laplace's probability function 430 Approximation by Poisson's probability function 431 Approximation, principle of least squares 422 Approximation, principle of moments 422 Arithmetical progression 79 Bayes’ Theorem 86 Bernoulli numbers 23 62 130 140 181 182 227 229 Bernoulli numbers by Cmi 229 599 Bernoulli numbers by Stirling numbers 219 236 Bernoulli numbers, ex-pressed by b 250 Bernoulli numbers, symbolical formula of 233 Bernoulli numbers, table of 234 235 Bernoulli polynomials into Boole polynomials 323 Bernoulli polynomials into Euler polynomials 308 Bernoulli polynomials into Fourier series 242 Bernoulli polynomials, expansion into Bernoulli polynomials first kind 276 Bernoulli polynomials, expansion into factorials 235 Bernoulli polynomials, extrema 240 Bernoulli polynomials, first kind 60 62 181 230 Bernoulli polynomials, generating function of 279 Bernoulli polynomials, limits 272 Bernoulli polynomials, multiplication formula of 252 Bernoulli polynomials, roots 240 Bernoulli polynomials, second kind 64 72 134 147 224 265 277 Bernoulli polynomials, symmetry 268 Bernoulli series 253 Bernoulli series, second kind 280 Bernoulli’s solution of numerical equations 494 Beta functions 50 80 Binomial coefficients 62—70 Binomial coefficients, Cauchy’s formula of 73 Binomial coefficients, generalised 70 Binomial moments 424 Binomial moments by Stirling numbers 267 147 Binomial moments, computation of 460 613 Binomial moments, expressed by Bernoulli numbers 249 278 Binomial moments, generating function of 258 279 284 Boole polynomials 64 317 321 Boole polynomials, expanded into Bernoulli polynomials second kind 321 Boole series 323 Boole’s first summation formula 315 354 Boole’s first summation formula, second summation formula 323 Cauchy’s formula for binomials 24 41 48 68 Cauchy’s formula, integral 41 Cauchy’s formula, rule for summing binomials 73 133 135 136 Cauchy’s formula, rule of multiplication of series 25 Changing the origin of intervals 219 Changing the origin of intervals the length of intervals 220 Combinations, difference equation giving number of 578 Construction of tables 363 Correlation, coefficient of 455 cot z expansion of 259 Cotes numbers 224 388 Cotes numbers, determined by Stirling numbers 514 Decomposition into partial fractions 34—40 335 Derivatives expressed by 197 Derivatives expressed by differences 164—165 Difference equation linear variable coefficients first order 576 Difference equation, complete 583 Difference equation, homogeneous by Laplace’s method 579 Difference equation, reducible 584 Difference equation, resolution by Andre’s method 587 Difference equation, resolution by generating functions 586 Difference equations by method of arbitrary constants 569 Difference equations with complex roots 554 Difference equations with multiple roots 549—552 Difference equations with negative roots 552 Difference equations, characteristic equation with single roots 542 Difference equations, genesis of 543 Difference equations, linear mixed 632 Difference equations, linear, constant coefficients, complete 557—564 Difference equations, linear, constant coefficients, homogeneous 545 Difference equations, particular solution obtained directly 564 Difference equations, resolved by generating functions 572 Difference of a function with negative argument 5 69 Difference of a product 94—98 Differences (advancing) 2 Differences (advancing), central 15 Differences (advancing), divided 18 Differences (advancing), receding 14 Differences expressed by derivatives 189—192 Differences expressed by means 9 Differences expressed by the operation 200 Differences expressed by values of the function 8 Digamma function 58—60 Digamma function by Bernoulli series, of the second kind 283 Digamma function by powers series 327 Digamma function by reciprocal powers 328 Digamma function expressed by Bernoulli series 256 Digamma function, sum of 1 Displacement 6 Endpanel interpolation formula 379 Euler numbers 23 300 Euler numbers limits of 302 Euler polynomials 62 115 288 Euler polynomials, extrema of 293 Euler polynomials, generating function of 309 Euler polynomials, inverse difference of 297 Euler polynomials, inverse means of 297 Euler polynomials, limits of 302 Euler polynomials, multiplication theorem of 311 Euler polynomials, roots of 293 Euler polynomials, symmetry of 292 Euler’s constant 27 55 58 129 130 148 341 Euler’s formula for f functions 55 83 Euler’s formula for trigonometric functions 90 Euler’s polynomials expanded into Bernoulli polynomials 295 Expansion of a function by decomposition into, partial fractions 34 40 Expansion of a function of functions 31 33 204 205 Expansion of a function, complex intergrals 40—41 Expansion of a function, difference equations 41—44 Expansion of a function, symbolical methods 11 Expansion of functions into Bernoulli polynomials 307 248 250 Expansion of functions into Bernoulli series 253 Expansion of functions into binomials 74 Expansion of functions into Boole polynomials 322 Expansion of functions into Boole series 323 Expansion of functions into Euler polynomials 307 Expansion of functions into Euler series 313 Expansion of functions into Legendre polynomials 434 Expansion of functions into Newton series 74 358 Expansion of functions into orthogonal series 447 Expansion of functions into polynomials 355 Expansion of functions into powers 29—34 Expansion of functions into reciprocal factorials 192 212 Expansion of functions into reciprocal powers 212 Exponential functions 87—88 Faa Bruno’s expansion of a function of function 33 205 Factorial moments determined by generating functions 208 Factorials 45—53 Factorials, computation of 52 Factorials, definition by gamma functions 56 Factorials, difference of 51 Factorials, expansion into powers 142 Factorials, mean of 52 Fibonacci numbers 548 First panel interpolation formula 378 Fourier series 242 426 463 Fourier series, Newton series 289 Functions expressed by differences 10 Functions expressed by means 10 Functions expressed whose differences or means are zero 94 Functions expressed, product of two 94—98 G polynomials 426 473 Gamma function 53—56 Gamma function, computation of 55 Generating functions 20 29 109 Generating functions of binomial coefficients 71 73 Generating functions, determination by difference equations 27 Graduation by least squares and orthogonal polynomials 456 Gregory’s formula of numerical integration 525 Hermite polynomials 63 426 467 Hospital’s rule 133 Hyperbolic functions 38 Incomplete B function 83—37 Indefinite sum 101 Indefinite sum by difference equation 109 Indefinite sum by inversion 103 Indefinite sum by summation by parts 105 Infinite series, differences and means of 110 Interpolation by Bessel's formula 373 Interpolation formula, general case 420 421 Interpolation formula, precision of 417—420 Interpolation in a double entry table 532 Interpolation, case of three variables 541 Interpolation, Everett's formula 376 Interpolation, formula needing no differences 390 Interpolation, Gauss' formulae 363 Interpolation, Newton's formula 361 Interpolation, Stirling's formula 374 Inverse difference 101 Inverse difference, Everett 381 Inverse difference, Formula needing no differences 411 Inverse difference, Lagrange 390 Inverse mean 111—116 Inverse mean of a function 306 Inversion of sums and series 183 185 Iteration, method of, for solving numerical equations 492 Lacroix’s difference equation giving the sum of x 596 Lagrange’s formula 360 Lagrange’s formula, interpolation formula 386 Lagrange’s formula, polynomial 385 Legendre polynomials 389 434 Legendre polynomials, roots of the 435 Leibnitz’ formula of higher derivatives 96 143 167 log, Bernoulli series, second kind 284 287 log, expansion into Bernoulli polynomials, second kind 280 log, tables 399 402 407 409 410 Maclaurin series 201 216 246 Maclaurin — Euler summation formula 260 265 Mean of a function 7 Mean of a function of a product 98—99 Mean of a function, central 15 Mean, arithmetical 433 Mean, binomial moment 448 Mean, orthogonal moment 450 Mean-square deviation 427 433 452 Median 433 Midpanel interpolation formula 397 MODE 433 Moments, actorial 424 Moments, binomial 424 Moments, computation of binomial moments 615 Moments, expressed by semi-invariants 211 Moments, power 163 164 812 Newton — Rapbson solution of numerical equations 489 Newton's binomial formula 49 Newton's binomial formula, expansion 26 75 76 77 79 164 189 219 357 Newton's binomial formula, expansion for unequal intervals 20 Newton's binomial formula, formula for two variables 531 Numerical integration 512 Numerical integration, Euler — Maclaurin formula 525 Numerical resolution of difference equations 527 Orthogonal polynomials 436 Orthogonal polynomials, central value of the 445 Partial difference equations 604 Partial difference equations four independent variables 638 Partial difference equations, Boole's symbolical method 616 Partial difference equations, Fourier, Legendre, Ellis' method 619 Partial difference equations, Laplace's method of generating functions 607 Partial difference equations, linear, constant coefficients 60 Partial difference equations, three independent variables 633 Partial differences 530 Pascal’s arithmetical triangle 612 Power moments expressed by 6 Power moments expressed by operations 197 Power series, sum of 246 Powers expressed by factorials 181 Probability by Stirling numbers 166 177 Probability function, binomial moments of 424 Probability function, expanded into G polynomials 483 484 Probability function, table of 400 403 408 Probability, coincidences 595 610 Probability, determination of, by sums 140 Probability, Examples on, Bayes' theorem 86 Probability, parcours 630 633 638 Probability, problem of 575 Probability, problem of points 608 Probability, repeated trials 86 599 615 Probability, ruin 550 627 Product of prime numbers, decomposition of 179 181 Progression, arithmetical 118 Progression, geometrical 124 Rational fraction, sum of 335 Reciprocal factorial, derivation of 337 Reciprocal factorial, expanded into reciprocal powers 193—195 Reciprocal factorial, integration of 194 338 Reciprocal factorial, sum of 121 Reciprocal powers, alternate sum of 244 Reciprocal powers, difference of 194 Reciprocal powers, sum of 194 244 214 325 338 Reciprocal powers, sum of, by Stirling numbers 338 Regula Falsi 366 486 Remainder of the expansion into a series of polynomials 356 Remainder of the expansion, maximum of 362 Rule of false position 366 486 Schlomilch's expansion formula 31 204 Semi-invariants of Thiele 204 210 Semi-invariants of Thiele, expressed by moments 211 Simmons theorem 87 Simultaneous linear difference equation 601 Stirling numbers of the second lcind 32 134 168 179 Stirling numbers, formulae containing 182 185—189 Stirling polynomials 224—229 Sum without repetition transformed 153—158 Summation by parts 105 106 107 Summation by parts of alternate function 108 140 320 324 Symbolical calc. 7—14 tan z, expansion of 259 Tangent coefficients 130 298 Taylor’s series 13 165 189 Tchebichef polynomial 389
Реклама
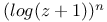expansion into powers 
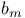numbers, table of 
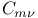numbers, table of 
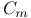, numbers, table of 
functions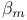 
numbers, table of 
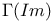numbers, table of 
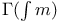numbers, table of 
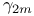numbers table of 
operation 
|
|
О проекте