|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Debnath L., Mikusinski P. — Introduction to Hilbert Spaces with Applications |
|
|
 |
| Предметный указатель |
Solution, stable 461
Solution, unstable 461
Solution, weak 296
Space spanned by  10 10
Space, 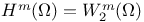 97 97
Space,  45 45
Space, 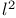 6 89 6 89
Space, ![$L^2([a, b])$](/math_tex/02f06fd4829bd46a8febfd8a753f702182.gif) 89 89
Space,  74 74
Space,  75 75
Space,  6 6
Space,  5 5
Space, 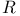 3 3
Space, ![$\mathcal{C}([a, b])$](/math_tex/28e58cac1cf62898a6a97842399a3bd582.gif) 89 89
Space, 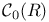 95 95
Space,  96 96
Space, Banach space 19
Space, C 3
Space, Euclidean 92
Space, finite dimensional vector space 10
Space, Hilbert 93
Space, infinite dimensional 10
Space, infinite sequence 6
Space, inner product 88
Space, non-separable Hilbert 125
Space, pre-Hilbert 88
Space, separable Hilbert 124
Space, Sobolev 96
Space, test function 285 294
Space, vector 4
Spectral theorem for self-adjoint compact operators 189
Spectral theorem for unbounded operators, Spectrum 177
Sphere 14
Spherical harmonics 377
Spherically symmetric potential 375
Spin 400
Square integrable functions 74 76
Square root of an operator 165
Stability criterion 463
Stable solution 461
Stampacchia 445
Standard deviation 359
State equation 452
State function 349 447
State transition matrix 449
State vector 347
States 345
Stationary point 425
Stationary state 362
Step function 38 75
Strictly convex norm 127
Strictly positive functional 143
Strictly positive operator 166
Strong convergence 25 97
Sturm — Liouville systems 257
subspace 5
Successive approximation 234
Summability kernel 113
Support 39
Symmetric bilinear functional 143
Symmetric operator 206
Synthesis of a pulse 271
Tautochronous motion 247
Telegrapher equation 299
Tent function 83
| Test function space 285
Theorem, Banach fixed point 30
Theorem, closed graph 208
Theorem, compatibility 407
Theorem, contraction mapping 30 225
Theorem, convolution 196
Theorem, Ehrenfest 375 383
Theorem, Fubini’s 78
Theorem, Hilbert — Schmidt 187
Theorem, implicit function 470
Theorem, Lax — Milgram 148
Theorem, Lebesgue dominated convergence 60
Theorem, Lions — Stampacchia 445
Theorem, Lyapounov 463
Theorem, mean value 415
Theorem, monotone convergence 59
Theorem, orthogonal projection 120
Theorem, Picard existence 228
Theorem, Plancherel 202
Theorem, Riesz representation 123
Theorem, Spectral 189 211
Theorem, virial 408
Theorem, Weierstrass approximation 17
Time-dependent Schrodinger equation 363
Time-dependent state vector 347
Time-evolution equation 381
Time-evolution operator 379
Time-invariant 447
Total angular momentum 403
Total energy 335 353
Total Hamilton operator 389
Transfer function 271
Transition matrix 449
Triangle inequality 11 91
Trigonometric Fourier series 112
Two-sided shift operator 214
Unbounded operators 203
Uncertainity 359
Uncertainty principle 360
Uniform convergence 12 25
Unitary operator 160
Unitary space 88
Universal constant 346
Unstable solution 461
Variables 345
Variational inequalities 443
Variational problems 311 411
Vector space 4
Vector subspace 5
Virial theorem 408
Volterra equation 236 246
Volterra equation of the first kind 223 246
Volterra equation of the second kind 224 237
Vorticity transport equation 322
Walsh functions 111
Wave equation 299 300 318
Wave function 349
Wave-particle duality 370
Weak convergence 97
Weak distributional convergence 289
Weak solution 296 311
Weierstrass approximation theorem 17
Weight function 253
Weighted average 357
wronskian 260
Zeeman effect 400
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте




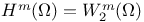

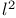
![$L^2([a, b])$](/math_tex/02f06fd4829bd46a8febfd8a753f702182.gif)




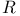
![$\mathcal{C}([a, b])$](/math_tex/28e58cac1cf62898a6a97842399a3bd582.gif)