|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Cayley A. — An elementary treatise on elliptic functions |
|
|
 |
| Предметный указатель |
Abel, linear and quadric transformations 322 325 375 376
Abel, linear and quadric transformations, irrational transformation 382
Addition see “Function (2)...(9)”
Arc of curve, determination of curves the arc of which represents elliptic integral of first kind 352 (Chap. xv.)
Arc of curve, representing integrals  , ,  (ellipse, hyperbola, lemniscate) 35 (ellipse, hyperbola, lemniscate) 35
Arithmetico-geometrical mean 332
Baehr’s formuls for multiplication of sn, en, dn 79
Circular functions, illustration by reference to 10
Definitions and Notations 1 (Chap. I.)
Definitions and Notations, amplitude, modulus, complementary modulus, parameter 3
Definitions and Notations, complete functions  , ,  4 4
Definitions and Notations, elliptic functions am, sin am, cos am,  am, or sn, en, dn 8 am, or sn, en, dn 8
Definitions and Notations, elliptic integrals  , ,  , ,  3 3
Definitions and Notations, Eu, Zu, 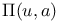 15 15
Definitions and Notations, K, K' 12
Definitions and Notations, \Theta u$, Hu 16
Differential equation of third order, satisfied by modulus in transformation of nth order 222
Differential equation, addition-equation 5 21
Differential equation, equation  339 (Chap XIV.) 339 (Chap XIV.)
Differential equation, partial, satisfied by  , H, &c, and the numerators and denominators in multiplication and transformation of sn, en, dn 226 (Chap. IX.). , H, &c, and the numerators and denominators in multiplication and transformation of sn, en, dn 226 (Chap. IX.).
Differential equation, satisfied by  , ,  , or by , or by  , ,  47 50 47 50
Differential equation, satisfied by multiplier 220
Differential equation, special equation 250
Dimidiation 72 see
Doubly infinite products see “Factorial”
Duplication 71 see
Duplication by two quadratic transformations 181
Euler, partition formula 290
Factorial formule 92 97
Factorial formule, doubly infinite product forms 101 300
Function, (1),  reduction to standard form 1 311 (Chap. xii.) reduction to standard form 1 311 (Chap. xii.)
Function, (10),  , Hu 142 (Ch. VI.) 226 , Hu 142 (Ch. VI.) 226
Function, (10),  , h expressed as q-functions 291 , h expressed as q-functions 291
Function, (10), connexion with sn, en, dn, Zu and 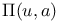 155 155
Function, (10), development in q-series 297
Function, (10), double factorial expressions 300
Function, (10), Hu introduced 156
Function, (10), multiplication 159
Function, (10), partial differential equations 229
Function, (10), properties of  150 152 150 152
Function, (10), transformation 306
Function, (11), connexion with  , Hu 161 , Hu 161
Function, (11), connexion with functions  , H 309 , H 309
Function, (11), numerators and denominator in multiplication and transformation of sn, en, dn 226 (Chap. rx.)
Function, (11), partial differential equations 235
Function, (11), verification for cubic transformation 245
Function, (12),  , H expressed as q-formulae 291 , H expressed as q-formulae 291
Function, (12), derivation of the q-formulas 282
Function, (12), q-functions 282 (Chap. xi.)
Function, (13), further theory 342
Function, (13), Lagrange’s integration 339
Function, (13), The general equation  339 (Chap. XIV.) 339 (Chap. XIV.)
Function, (2), addition - equation 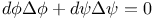 21 (Chap. II.) 21 (Chap. II.)
Function, (3),  , march of function 41 , march of function 41
Function, (3), addition 103
Function, (3), imaginary modulus  367 367
Function, (3), properties as function of k 46
Function, (3), quadric transformation, &c 327
Function, (4),  41 (see also “Infra march 41 (see also “Infra march
Function, (4), addition 104
Function, (4), properties as function of k 46
Function, (4), quadric transformation, &c 327
Function, (5),  see also “(9) infra” see also “(9) infra”
Function, (5), addition 104
Function, (5), addition of parameters, and reduction to standard form 117
Function, (5), interchange of amplitude and parameter 133
Function, (5), outline of further theory 108
Function, (5), reduction of parameter to form  114 114
Function, (6), gd u, sg u, eg u., addition and other properties 56
Function, (7), addition and subtraction formulae 63
Function, (7), anticipation of doubly infinite product forms 101
Function, (7), connexion with  , Hu 155 156 , Hu 155 156
Function, (7), dimidiation 72
Function, (7), duplication 71
Function, (7), factorial formulae 92
| Function, (7), functions of u + (0, 1, 2, 3) K + (0, 1, 2, 3) iK' 69
Function, (7), imaginary transformation 68
Function, (7), multiplication 78
Function, (7), n-thic transformation 251 (Ch. x.).
Function, (7), new form of same 97
Function, (7), periods 4K, 4iK' 66
Function, (7), quadric transformations 183
Function, (7), sn u, en u, dn u 63 (Chap. IV.)
Function, (7), triplication 77
Function, (8), addition 107
Function, (8), connexion with  113 113
Function, (8), Em, Zu, connexion with  107 107
Function, (8), further theory 147
Function, (9), 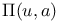 142 (Chap. VI.). 142 (Chap. VI.).
Function, (9), 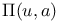 expressed in terms of Qu 151 expressed in terms of Qu 151
Function, (9), addition of amplitudes 157
Function, (9), addition of parameters 157
Function, (9), connexion with  107 107
Function, (9), connexion with 6m 113
Function, (9), interchange of amplitude and parameter 159
Function, (9), values of  for for 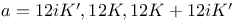 144 144
Gauss, the arithmetico - geometrical mean 331 338
Glaisher, proof of Legendre’s relation between complete functions  , &c 49 , &c 49
Glaisher, tables of theta functions 155
Gordan, integral reducible to elliptic functions 369
Gudermann 44 58
Gudermannian 58 (see also “Function (6)”)
Imaginary transformation, Jacobi’s 68
Imaginary, reduction of given, to form  114 114
Integrals involving root of a quintic function and reducible to elliptic integrals 360 (Chap. XVI.)
Integrals involving root of a quintic function and reducible to elliptic integrals, involving root of a sextic function 369
Integration, general theorem of 354
jacobi 16 18 19 23 28 66 150 176 220 223 224 227 323
Kummer, formula in hypergeometric series 55
Lagrange, integration of differential equation  339 339
Landen’s theorem 30 327
Legendre, his relation between complete functions, 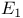 , ,  , , 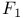 , ,  , formula relating to third kind of elliptic integral 119 121 134 , formula relating to third kind of elliptic integral 119 121 134
Legendre, proof of addition-equation by spherical triangle 27
Legendre, reduction of differential expression to standard form 314
Liouville, formula for arc of curve 40
Modular equation or relations, cubic transformation 188 195 206
Modular equation or relations, linear transformation 322
Modular equation or relations, odd-prime transformation 45 200 275 278
Modular equation or relations, quadric transformation 45 179
Modular equation or relations, quintic transformation 192 195
Modular equation or relations, septic transformation 194
Modular equation, differential equation of third order satisfied by the transformed modulus 222
Modular equation, properties of 200
Modular equation, verification for quadric transformation 223
Multiplication from two transformations 201 280
Multiplication of sn, en, dn 78 86
Multiplication tables 80 81
Multiplier in cubic, &c. transformations 203
Multiplier, differential equation satisfied by 220
Multiplier, Jacobi’s relation 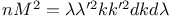 218 218
Multiplier, relation between M, K,  , E, G 224 , E, G 224
Notation explained 5
Numerical instance for complete functions 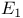 , , 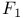 , and for incomplete F 337 , and for incomplete F 337
Richelot, representation of given imaginary quantity in form  117 117
Roberts, M., integral reducible to elliptic functions 369
Serret, formula for arc of curve 40
Tables of the theta functions 155
Transformation of functions, H,  306 306
Transformation, combined, and irrational 379
Transformation, cubic 188 195 206 216 245
Transformation, general outline 164 (Chap. VII.)
Transformation, Landen’s theorem 30 327
Transformation, linear transformation of integral 312 319 370
Transformation, multiplication formulae obtained from two transformations 280
Transformation, odd or odd-prime, by the n-division of the complete functions 251 (Chap. x.)
Transformation, quadric 179 (Chap viii.) 323 376
Transformation, quintic 191 197
Transformation, septic 194
Transformation, two transformations leading to multiplication 201
Triplication 77 (see also “Function (7)”)
Walton, proof of addition-equation 22
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 ,
,  (ellipse, hyperbola, lemniscate)
(ellipse, hyperbola, lemniscate)  ,
, 
 am, or sn, en, dn
am, or sn, en, dn 
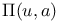

 , H, &c, and the numerators and denominators in multiplication and transformation of sn, en, dn
, H, &c, and the numerators and denominators in multiplication and transformation of sn, en, dn  reduction to standard form 1
reduction to standard form 1  , Hu
, Hu 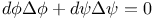



 for
for 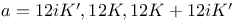
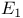 ,
,  ,
, 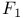 ,
,  , formula relating to third kind of elliptic integral
, formula relating to third kind of elliptic integral 
 , E, G
, E, G