|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Данфорд Н., Шварц Дж.Т. — Линейные операторы (том 2) Спектральная теория |
|
|
 |
| Предметный указатель |
Кембл 757 984
Кемп 984
Кернер 984
Кёте 984 985
Килпи 985
Киносита 985
Кларксон 950 985
Клейнекке 985
Кли 985
Клиффорд 996
Кнезер 749 754 756 985
Кнопп 985
Кобер 985
Ковалевский 985
Кодаира 83 316 469 516 521 530 548 552 558 656 658 661 691 752 754 755 799 980 986
Коддингтон 599 600 665 670 752 754—756 986
Козлов, В.Я. 986
Коллац 84 986
Коллинз 986
Колмогоров, А.Н. 966 986
Коматудзаки 986
Комплексно присоединенный формальный дифференциальный оператор с частными производными (804)
Комплексно сопряженное распределение XIV.3.7 (814)
Кон 979
Конечная область оператора XII.7.4 (415)
Конечномерная функция XI.1.3 (96)
Коосис 327 987
Кордес 987
Косинус-теорема Фурье XII.5.33 (554)
Костюченко, А.Г. 442 753 779 780 791 966 987
Котляр 987
Коши 17 18 212 225 353 547 598 794—797 799 800 870 914—916 936 987
Коэн, И. 987
Коэн, Л. 987
Коэффициент Фурье распределения XIV.3.38 (829) XIV.3.42 834)
Крамер, В. 987
Крамер, Г. 987
Крамерс 757 987
Красносельский, М.А. 242 438 440 753 755 987 988 989
Кратнопериодическое распределение XIV.3.29 (826)
Кратность собственного значения (61)
Кратность упорядоченного представления Х.5.9 (72) XII.3.15
Крачковский, С.Н. 988
Крейн, М.Г. 5 159 251 327 329 438 440 441 752 753 755 786 791 966 969 970 987—989
Кристиан 83 989
Кронин 990
Кук 82 83 990
Кунисава 990
Купер 83 88 425 441 990
Купмен 83 85 990
Курант 990
Куратовский 990
Курош, А.Г 990
Кэли 438—441
Кюршак 990
Лаасонен 990
Лаврентьев, М.А. 990
Лагерр 552 990
Лагранж 273 747 748 753
Лакс, А. 990
Лакс, П. 779 914 991
Лалеско 242 328
Ламсон 991
Лангер 757 956 991
Ландау 756 991
Лаплас 796 797
Ласаль 991
Латшоу 754 991
Лаурикайнен 991
Лебег 52 67 82 106 107 133 209 210 218 237 289 290 293 295 303 304 314 321 336 366 377 422 500 535 609 632 702 732 744 749 790 806 807 809 811 812 826 833 858 875 911 991
Леви, Б. 991
Леви, П. 32 991
Левинсон 434 599 600 665 752 754—756 786 792 957 986 992
Левитан, Б.М. 752 753 755 779 780 786 788 790 791 793 966 992
Лежандр 687 748
Лежанскин 992
Лейбниц 452 453 456 594 802 825 867 868 871 881 883 901 902 912 926 929
Лейтон 992
Лейя 993
Лемма Аренса IX.3.5 (27)
Лемма Каратеодори XI.6.32 (202)
Лемма Лионса XIV.6.16 (892)
Лемма Фрагмена — Линделёфа XI.6.33 (203) XI.9.28
Леньель 83—85 993
Лере 993
Лефшец 993
Лёвиг 992
Лёвнер 992
Ли 309 312 313
Ливингстон 993
Лившиц, М.С. 329 330 442 753 960 993
Лидер 993
Лидский, В.Б. 753 755 993
Линдгрен 980
Линделёф 198 201 203 276
Линейно независимые граничные условия XII.4.25 (403)
Лионс 891 892
Липшиц 719
Литлвуд 163 166 167 237 312 331 338 343 347 349 350 356 994 1029
Лиувилль 199 265 457 705 707 717 718 747 748 753—755 757 768 780 781 994
Лифшиц, И.М. 994
Лихтенштейн 994
Ловалья 994
Лоран 199 200 265 323 672
Лоренц 994
Лорх 35 83 994 1013
Лузин, Н.Н. 385 509
Лукомский, Т.И. 995
Люмер 87 90 995 1029
Люмис 35 83 309 313 316 326 327 441 442 995
Ма 995
Маак 995
Маеда 441 995 1005
Мазани 995
Мазур 954 995 1038
Майерс 996
Майкал 34 996
Майкл 38 87 996
Мак-Даффи 996
Мак-Лейн 956 996
Мак-Фейл 996
Мак-Шейн 83 996
Мак-Эвен 997
Макай 996
Макинтайр 996
Макки 326 327 980 996
Максимальный вектор гильбертова пространства Х.5.6 (67)
Максимальный симметрический оператор (439)
Малявен 327 997
Мандельбройт 327 997
Манроу 997
Маринеску 977 997
Марков, А.А. 997
Маркушевич, А.И. 997
Мартин, Р. 34 996
Мартин, У. 980 981
Маруяма 998
Марцинкевич 250 331 334 337 346—349 998
Марчевский 998
Марченко, В.А. 753 755 780 786 791 998
Маслов, А.С. 998
Маслов, В.П. 85 998
Матрица Якоби (442)
Матричные элементы представления топологической группы (310)
Маутнер 437 799 875 998
Махарам 998
Медведев, Ю.Т. 998
Меддаус 998
Мера упорядоченного представления Х.5.9 (71) XII.3.15
Мера Хаара на бикомпактной группе XI.1.2 (96)
| Мергелян, С.Н. 998
Меркил 327 998
Меррей 36 38 436 999
Мерсер 250
Микусинский 999
Миллер, Д. 972 999
Миллер, К. 999
Милн 757 778 999
Мильграм 991
Мильман 753 755 960 989 999
Мимура 84 978 999
Минковский 171 233 256 1000
Минлос 1000
Миранда 1000
Митягин, Б.М. 442 891 1000
Михлин, С.Г. 204 347 1000
Мишоу 1000 1027
Миядера 1000
Множества кратности упорядоченного представления Х.5.9 (71 72) XII.3.15
Мозер 1000
Мозес 786 983 1000
Молчанов, А.М. 730 753 755 760 1000
Момент (417)
Монна 1000
Монтролль 1001
Мор 754 1001
Морс, А. 950 972 1001 1038
Морс, М. 1001
Московиц 1001
Мур, Р. 1001
Мур, Э. 1000
Мюнц 1001
Нагата 1001
Нагумо 34 1001
Наймарк, М.А. 5 6 26 27 35 38 39 48 88 313 327 390 428 438 441 453 754 756 758 760 761 772 773 774 775 967 1001
Накамура 83 84 85 437 441 442 1002
Накаяма 83 978 1003
Натан 1003
Натансон, И.П. 1003
Нахбин 1003
Начальная область оператора XII.7.4 (415)
Нейгауз, М.Г. 1003
Нейман, Дж. 36 38 82 83 84 89 90 309 316 329 408 425 430 436 437 439 440 441 514 751 753 756 958 972 978 999 1003 1029
Нейман, К. 1004
Неймарк, Ф. 1004
Немыцкин, В.В. 1587 753 1004
Неотрицательный симметрический оператор XII.5.1 (407)
Непрерывный спектр оператора Х.3.1 (56) (353)
Неравенство Адамара X 1.6.12 (178)
Неравенство Гайнца (92)
Неравенство Гординга XIV.6.10 (882)
Неравенство Кальдерона — Зигмунда XI.7.11 (224)
Неравенство Карлемана XI.6.27 (197)
Неравенство Пэли — Литлвуда XI. 11.25 (343)
Неравенство Рисса, М. XI.7.8 (219)
Неравенство Шварца (939)
Никович, И.А. 329 1004
Никодим 70 74 364 525 1004
Николеску 1005
Никольский, В.Н. 1005
Никольский, С.М. 1005
Ниман 1005
Ниренбург 204 950 1005
Норма Гильберта — Шмидта XI.6.1 (169)
Нормальный оператор в гильбертовом пространстве IX.3.14 (30) (39)
Носитель распределения XIV.3.11 (816) XIV.3.32
Нусбаум 972 1005
Ньюбург 1005
Ньютон 791 1005
Область регулярности (440)
Обобщенное неравенство Карлемана XI.9.24 (274)
Общая спектральная теорема Х.2.1 (48)
Огасавара 1006
Ограниченный сверху (снизу) симметрический оператор XII. 5.1 (407)
Ограниченный сверху (снизу) симметрический формальный дифференциальный оператор XIII.7.20 (617)
Одэн 1006
Окстоби 316 1006
Оно 36 1006
Оператор Гильберта — Шмидта XI.6.1 (169)
Операторное исчисление (43)
Операторы  , , 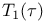 ХШ.2.8 (458) ХШ.2.8 (458)
Операторы обобщенного сдвига (792)
Определяющая система решений XIII.5.22 (540 541)
Определяющее уравнение дифференциального оператора (599 600) (670)
Орихара 1006
Орлич 951 957 995 1006
Орлов, С.А. 1006
Ортогональное дополнение множества (940)
Ортонормированное множество (942)
Ортонормированный базис (944)
Остаточный спектр оператора Х.3.1 (56) (353)
Оухар 1006
Охира 1006
О’Нилл 1006
Параболический оператор (789)
Паркер 242 1007
Пародии 239 1007
Парсеваль 748
Паули 1007
Пеано 753 1007
Пейс 734 1007
Пек 1007
Перестановочность операторов (90)
Перрон 240
Петер 93 96 309 311 1007
Петтис 115 972 1007
Пик 241
Пиконе 749 756 1007
Пинкерле 1007
Пинскер, А.Г. 981 1007
Пирс 1008
Питт 1008
Планшерель 93 119 129 132 133 134 140 142 143 150 159 205 215 219 221 228 232 313 321 324 325 326 344 594 734 755 830 831 1008
Плеснер, А.И. 85 437 441 1008
Повзнер, А.Я. 753 791 799 1008
Пойа 349 756 1008 1029
Показатели дифференциального оператора (671)
Поллард 432 433 1008
Полная система представлений топологической группы (311)
Полное множество (942)
Полное множество граничных значений оператора XII.4.22 (402)
Полное множество граничных значений формального дифференциального оператора XIII.2.17 (465)
Положительная  -матричная мера XIII.5.6 (503 504) XIII.5.12 -матричная мера XIII.5.6 (503 504) XIII.5.12
Положительно определенный оператор в гильбертовом пространстве Х.4.1 (59)
Положительный оператор в гильбертовом пространстве Х.4.1 (59)
Полуограниченный симметрический оператор XII.5.1 (407)
Полупростая банахова алгебра IX.2.5 (19)
Полярное разложение (91)
Понтрягин, Л.С. 309 314 323 324 326 1008
Порядок особенности уравнения (599)
Потапов, В.П. 993
Поттер 1008
Прайс 1008
Представление топологической группы (309)
Представление топологической группы неприводимое (310)
Преобразование Кэли (438)
Принцип замены меры (47)
Проблема моментов (417)
Продолжение оператора (87)
Произведение дифференциальных операторов с частными производными (802)
Пространство  XIII.1.2 (447) XIII.1.2 (447)
Пространство  (515) (515)
Пространство  XIII.5.8 (504 505) (515) XIII.5.8 (504 505) (515)
Прюфер 1008
Прямая сумма гильбертовых пространств (948)
Прямая сумма представлений топологической группы (310)
Птак 1009
Пуанкаре 1009
Пул 599 670 1009
Путнам 91 730 752 756 764 775 1009 1030
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 ,
, 
 -матричная мера
-матричная мера