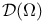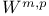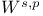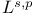|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Adams R.A. — Sobolev Spaces |
|
|
 |
| Предметный указатель |
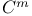 -regularity 67 -regularity 67
 -regular 232 -regular 232
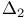 -condition 231 232 -condition 231 232
 -fat cube 161 -fat cube 161
 -algebra 13 -algebra 13
 -net 7 -net 7
Almost everywhere 14
Approximation theorem 14
Approximation theorem for Lebesgue spaces 28 31
Approximation theorem for Orlicz spaces 240
Approximation theorem for Orlicz — Sobolev spaces 247
Approximation theorem for Sobolev spaces 52 54 57 205 207
Aronszajn, N. 219
Ascoli — Arzela theorem 10
Banach algebra 115
Banach space 4
Besov space 177 223
Besov, O.V. 218 223
Bessel potential 219 220
Bochner integral 178
Boundary 2
Bounded operator 9
Browder, F.E. 70 79
Caiderdn, A.P. 83 89 91 219 221
Caldcron — Zygmund inequality 91
Calder6n extension theorem 91
Capacity 152
Cartesian product 8
Cauchy sequence 4
Characteristic function 14
Clark, C.W. 175
Clarkson’s inequalities 37
Compact imbedding 9
Compact imbedding theorem for continuous function spaces 11
Compact imbedding theorem for Orlicz — Sobolev spaces 249 252 256 259
Compact imbedding theorem for Sobolev spaces 144 151 157 162 163 166 167 170
Compact set 6
Compact support 2
Complementary N-function 229
Complete orthonormal system 173
Completeness 4
Completeness of Lebesgue spaces 26
Completeness of Orlicz spaces 234
Completeness of Orlicz — Sobolev spaces 246
Completeness of Sobolev spaces 45
Completion 4
Complex interpolation method 177 221
Cone 65 96
Cone property 66
Cone property, uniform 66
Cone, standard 124
Conjugate exponent 23
Conjugate N-function 248
Continuous functional 3
Convergence in the sense of 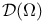 19 19
Convergence, norm 4
Convergence, weak 6
Convexity, local 3
Convexity, uniform 7 34 46
Convolution 29 90 199
Countably additive 13
Cusp 122 123
Cusp, exponential 122
Cusp, standard 124
Cylindrical coordinates 124
Dense 4
Derivative of a distribution 20
Derivative, distributional 21 179
Derivative, weak 21
distribution 19
Distribution, tempered 220
Distributional derivative 21 179
Domain 1
Dominated Convergence Theorem 17
Dominating N-function 231
Donaldson, T.K. 247
Dual space 3
Dual space of a Lebesgue space 40 41
Dual space of a Sobolev space 48—51
Dual space of an Orlicz space 238
Dual space of an Orlicz — Sobolev space 247
Ehrling, C 70 75 79
Embedding see “Imbedding”
Equivalent N-function 231
Equivalent norm 4 8
Equivalent norm for Sobolev spaces 79 158 214 223
Essential rate of increase 231
Essential supremum 24
Essentially bounded 24
Extension operator 83
Extension theorem 84 88 91 211
Fatou’s Lemma 17
Finite cone 65
Finite width 158
Flow 169
Fourier transform 220
Fractional order spaces 177
Fractional order spaces, Besov spaces 223
Fractional order spaces, Nikoskii spaces 225
Fractional order spaces, Sobolev spaces 204 206
Fractional order spaces, spaces of Bessel potentials 219 221
fringe 161 165
Fubini’s Theorem 18
Functional 3
Gagliardo, E. 67 68 70 75 95 99 101
Hahn — Banach extension theorem 6
Hestenes, M. 83
Hilbert space 5
Hilbert — Schmidt imbedding 175 176
Hilbert — Schmidt operator 174
Holder condition 10
Holder’s Inequality 23 234
Holder’s inequality, reverse form 24
Homogeneous function 91
Imbedding 9 96
Imbedding constant 97
Imbedding inequality, weighted norms 128 133 136 138
Imbedding theorem for Besov and Nikorskii spaces 224—226
Imbedding theorem for continuous function spaces 11
Imbedding theorem for cusp domains 126 127
Imbedding theorem for Lebesgue spaces 25
Imbedding theorem for Orlicz spaces 234 237
Imbedding theorem for Orlicz — Sobolev spaces 249 252 255 256 259
Imbedding theorem for Sobolev space 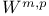 97 242 97 242
Imbedding theorem for Sobolev space 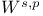 216—219 216—219
Imbedding theorem, direct and converse 217—219
Imbedding, compact 9 (see also “Compact imbedding”)
Imbedding, compact, theorem, Hilbert — Schmidt 175 176
Imbedding, compact, theorem, trace 96
Infinitesimal generator 181
Inner product 5
Integrability, Bochner 179
Integrability, Lebesgue 15 17
Integrability, local 19 179
Integral, Bochner 178 179
Integral, Lebesgue 15 17
Interpolation inequality 70 74 75 78 79 81 82
Interpolation method, complex 177 221
Interpolation method, real 177
Interpolation method, trace 178 186
Interpolation space 188
| Interpolation theorem between Banach spaces 188 222
Interpolation theorem between spaces 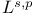 222 222
Interpolation theorem between spaces 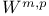 74 75 78 79 74 75 78 79
Interpolation theorem involving compact subdomains 81 82
Isometric isomorphism 4
Kernel 204 214—218
Kondrachov, V.L 143
Kondrachov, V.L, Rellich — Kondrachov theorem 144
Lebesgue dominated convergence theorem 17
Lebesgue integral 15 17
Lebesgue measure 13 14
Lebesgue spaces 22 24
Leibniz formula 2 21
Lichenstein, L. 83
Linear functional 3
Lions, J.L. 56 178 184 219
Lipschitz property 66
Lizorkin, P.I. 218
Local integrability 19 179
Localization theorem 207
Locally convex TVS 3
Locally finite 65
Lusin’s theorem 14
Luxemburg norm 234 253
m-Smooth transformation 63
Magenes, E. 178 219
Maurin, K. 174
Measurable function 14 17 178
Measurable set 13
Measure 13
Measure, complex 13
Measure, Lebesgue 14
Measure, positive 13
Meyers, N. 45 52
Minkowski’s inequality 23
Minkowski’s inequality, reverse form 24—25
Mollifier 29
Monotone Convergence Theorem 16
Morrey, C.B. 95 98
Multi-index 1
N-function 227 228
Nikollskii, S.M. 177 225 226
Nirenberg, L. 70 75
Norm 3
Norm, equivalence 4 8 79 158 214 223
Normable space 4
Normed dual 5
Normed space 4
Operator 8
Operator, bounded 9
Operator, compact 8
Operator, completely continuous 9
Operator, extension 83
Operator, imbedding 9
Orlicz class 232
Orlicz space 227 233 236
Orlicz — Sobolev space 246—247
Orthonormal system 173
Parallelepiped 65
Parallelogram law 5
Partition of unity 51
Polar set 56
Precompact set 7 31 33 242
Product, cartesian 8
Product, inner 5
Quasibounded domain 148
Quasicylindrical domain 159
Radon — Nikodym theorem 17
Reflexivity 6
Reflexivity of Lebesgue spaces 42
Reflexivity of Orlicz spaces 240
Reflexivity of Orlicz — Sobolev spaces 247
Reflexivity of Sobolev spaces 47 205
Reflexivity of trace interpolation spaces 189—190
Regularization 29
Rellich — Kondrachov theorem 144
Rellich, F. 143
Riesz representation theorem for Hilbert space 5
Riesz representation theorem for Lebesgue spaces 40 41
Scale of spaces 188
Schwartz distribution 18 19
Second dual 6
Seeley, R. 83 86
Segment property 54 66
Semigroup of operators 180
Separability 4
Separability of Lebesgue spaces 28
Separability of Orlicz spaces 240
Separability of Orlicz — Sobolev spaces 247
Separability of Sobolev spaces 47
Serrin, J. 45 52
Simple extension operator 83 91
Simple function 14 178
Smith, K.T. 219
Sobolev conjugate N-function 248
Sobolev imbedding theorem 95 97
Sobolev imbedding theorem, limiting case 242
Sobolev inequality 104
Sobolev space 44
Sobolev space, equivalent definitions 52
Sobolev space, fractional order 177 204 205 206
Sobolev space, integral order 44
Sobolev space, negative order 50 51
Sobolev, S.L. 45 95
Spherical coordinates 130
Spiny urchin 151—152
Stone — Weierstrass theorem 10
streamline 169
Strong extension operator 83 84
Strong local Lipschitz property 66
subspace 5
Support 2
Tempered distribution 220
Tesselation 106 161
Testing function 19
Topological vector space (TVS) 2
Total extension operator 83 88
Trace 96 185 186
Trace on a subspace 96 112
Trace on the boundary 113 114 215—217
Trace, higher-order 196 198
Trace, interpolation method 178 186
Trace, interpolation space 186 198
Transformation of coordinates 63—64
Trudinger, N.S. 228 242 247
Uniform 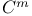 -regularity 67 -regularity 67
Uniform cone property 66
Uniform convexity 7
Uniform convexity of Lebesgue spaces 34 38
Uniform convexity of Sobolev spaces 47
Uspenskii, S.V. 218
Vector sum of Banach spaces 184
Volume 14
Weak convergence 6
Weak derivative 21
Weak sequential compactness 7
Weak topology 6
Weak-star topology 3 19
Young’s function 227 253
Young’s inequality 230
Young’s theorem 90
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



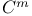 -regularity
-regularity  -regular
-regular 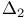 -condition
-condition  -fat cube
-fat cube  -algebra
-algebra  -net
-net