|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Baker G.A., Graves-Morris P. Ч Pade approximants (vol. 2) |
|
|
 |
| ѕредметный указатель |
 -Algorithm I: 80Ч84 -Algorithm I: 80Ч84
 -Algorithm I: 76Ч80 84Ч90 -Algorithm I: 76Ч80 84Ч90
 -Algorithm for vector sequences II: 55 -Algorithm for vector sequences II: 55
 -Algorithm, generalized II: 14Ч16 -Algorithm, generalized II: 14Ч16
A-stability II: 151
Acceleration of convergence I: 16Ч17 69Ч90
Accuracy, numerical I: 58Ч65
Accuracy-through-order I: 1Ч2
AitkenТs 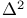 method I: 69Ч74 method I: 69Ч74
Algorithms for rational interpolation II: 6Ч17
Anharmonic oscillator II: 170Ч171
ArzelaТs theorem I: 175
Associated continued fraction I: 127
Asymptotic convergence I: 200
Asymptotic expansion I: 221
Backward recurrence method I: 115
Baker algorithm I: 66
Baker definition I: 21Ч22 II:
Baker Ч Gammel approximants II: 21Ч32 63
Baker Ч Gammel approximants, asymptotic II: 30Ч31
Baker, Gammel and Wills, conjecture of I: 286
Baker, Gammel and Wills, theorem of I: 32Ч33
BeardonТs theorems I: 237
Behte Ч Salpeter equation II: 108Ч113
Bigradients I: 37Ч42 136Ч137
Bigradients, polynomial I: 39
Binomial function I: 139 144
Biorthogonal algorithm II: 76Ч79
BLOCKS I: 24Ч31
C(L/M), definition of I: 21
C-fraction I: 127
C-table I: 22Ч23 29 31
Calculation of Pade approximants, algebraic I: 8Ч14 43Ч48 66Ч68
Calculation of Pade approximants, numerical I: 61Ч68
Canterbury approximants II: 41Ч45
Capacity I: 274Ч284
Cardioid theorem I: 151
CarlemanТs criterion for Hamburger series I: 223
CarlemanТs criterion for Stieltjes series I: 200Ч202
CarlemanТs criterion, application of II: 169
CartanТs lemma I: 274
Cauchy Ч Binet formula I: 239Ч240
Cauchy Ч Jacobi problem II: 1
Characteristic function II: 128Ч132
Chebychev see УTchebyscheffФ
Chisholm approximants II: 41Ч43
Chordal metric I: 256Ч263
Clenshaw Ч Lord algorithm II: 58Ч60
Coefficient problem I: 65 II:
Collocation II: 138Ч145
Complementary error function I: 140 144
Continued fractions I: 103Ч157
Continued fractions, associated I: 127
Continued fractions, contraction of I: 127 147
Continued fractions, convergents of see УConvergentsФ
Continued fractions, corresponding I: 127
Continued fractions, definition I: 104Ч105 107
Continued fractions, divergence condition for I: 148
Continued fractions, elements of I: 104 119
Continued fractions, equivalence transformation of I: 105Ч107
Continued fractions, periodic I: 117 138
Continued fractions, recurrence relations for I: 106 109 135
Continued fractions, regular corresponding I: 127
Continued fractions, repeating I: 117Ч138
Continued fractions, summation formula I: 115Ч116
Continued fractions, terminating I: 104
Convergence in capacity I: 274Ч284
Convergence in measure I: 263Ч274
Convergence of row sequences I: 238 261
Convergents I: 104 111Ч112 117Ч119
CordellierТs identity I: 88
Crank Ч Nicholson methods II: 145Ч153
Critical point methods I: 55Ч57 59Ч61 II: 178
D(m, n), definition of I: 162
D-log Pade approximants I: 55 II:
Dawson integral I: 141
Dawson integral, generalized II: 19
de MontessusТs theorem I: 241Ч252
de MontessusТs theorem, generalization of I: 254 II:
Defect I: 53Ч55 58Ч59
Deficiency index I: 20
Density function, construction of I: 180Ч181
Determinancy of moment problem I: 17 179 193 197Ч207
Determinantal formulas for Pade approximants I: 4Ч8 43Ч48
Determinantal identities for Stieltjes series coefficients I: 165Ч166
Determinantal inequalities I: 227 235
Determinantal inequalities for Hamburger series coefficients I: 227 235
Determinantal inequalities for Stieltjes series coefficients I: 208 209
Diagonal sequences I: 236
Diffusion processes II: 145Ч153
Divergence condition I: 148 156Ч157
Divided differences II: 2
Duality I: 31 236
Equicontinuity I: 174Ч176
Equicontinuous sequences I: 210 261
Equivalence transformation I: 105Ч106
Error formula for Pade approximants of Hamburger series II: 128Ч129
Error formula for Pade approximants of Stieltjes I: 185 189Ч193 II:
Error formula for Pade approximation I: 6 250
Error formula for Pade approximation, from variational principles II: 103Ч106
Error function I: 141 II:
Essential singularity I: 49
Euclidean algorithm I: 66 134Ч135
Euler Ч Maclaurin sum formula II: 130
EulerТs corresponding fraction I: 137Ч139
EulerТs function and series I: 17Ч18 200Ч202
EulerТs recurrence theorem I: 106
EulerТs summation formula I: 115Ч116
Existence of Pade approximants I: 27
Exploding vacuum II: 166Ч167
Exponential approximants II: 28
Exponential function, continued fractions for I: 139Ч143
Exponential function, Pade approximants for I: 8Ч14
Exponential function, Saff Ч Varga theorems for I: 229Ч233
Exponential integral, continued fraction for I: 140 144 II:
Exponential integral, first order I: 186
Extended Stieltjes series see УHamburger seriesФ
Factorization II: 43
Fisher approximants II: 45
Forward recurrence method I: 114Ч115
Frobenius definition I: 20 22
Frobenius identities I: 85 90Ч93
Gamma function, BinetТs formula for I: 202Ч205
Gammel Ч Guttman Ч Gaunt Ч Joyce approximants II: 33Ч36
GammelТs counterexample I: 285
Gaussian quadrature II: 127Ч132
General C-fraction I: 129
Gnomic theory II: 74
GreenТs functions, bound-state II: 113
GreenТs functions, bound-state, partial wave, free II: 89
GreenТs functions, bound-state, partial wave, Jost solution II: 90
GreenТs functions, bound-state, partial wave, momentum space II: 114
GreenТs functions, bound-state, partial wave, standing wave, free II: 89
GreenТs functions, bound-state, S-wave, exponential potential II: 98
GreenТs functions, bound-state, three-dimensional, free II: 81
GreenТs functions, bound-state, three-dimensional, relativistic, free II: 108
GreenТs functions, bound-state, three-dimensional, relativistic, standing wave, free II: 109
GreenТs functions, bound-state, three-dimensional, standing wave, free II: 85
GregoryТs series I: 78 81
HadamardТs determinant theorem I: 39Ч42 243
Hamburger functions as real J-fractions I: 225
Hamburger moment, definition of I: 208 222
Hamburger series, definition of I: 208 222
HamburgerТs theorem I: 221
Hankel determinant I: 7 41
Hankel matrix, condition number of I: 64Ч65
HardyТs puzzle I: 78Ч80
Hausdorff measure,  -dimensional I: 283 -dimensional I: 283
Hausdorff moment problem I: 193Ч196
Herglotz functions I: 225Ч227
| HermiteТs formula I: 250 II:
High field expansions II: 179
Hilbert space methods II: 46 68Ч72 103Ч107
Homographic invariants I: 32Ч33 II: 45 53
Hughes Jones approximants II: 43Ч45
Hyperbolic tangent I: 139 143Ч144
Hypergeometric functions I: 141Ч147 197Ч198
Hypergeometric functions, 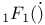 , Pade approximants of I: 43 47 142Ч147 154 II: , Pade approximants of I: 43 47 142Ч147 154 II:
Hypergeometric functions, 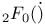 , Pade approximants of I: 43 47 141Ч147 154Ч155 , Pade approximants of I: 43 47 141Ч147 154Ч155
Hypergeometric functions, 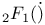 , Pade approximants of I: 43Ч47 141Ч147 156 , Pade approximants of I: 43Ч47 141Ч147 156
Identities for neighboring approximants I: 90Ч96
Inclusion regions I: 171 206
Incomplete gamma function I: 140 141 145 II:
Inequalities for density function II: 132Ч138
Inequalities for moments I: 186
Integer moment problem I: 196Ч197
Integral equations II: 64Ч79
Interlacing I: 168Ч169 210 227 II:
Invariance, homographic I: 32Ч33 II: 45 53
Inverse hyperbolic tangent I: 140 144
Inverse tangent I: 139 144 II:
J-fraction I: 128
Jost method II: 121Ч122
K-matrix II: 85 107 110Ч112
Kernels, compact II: 67Ч72
Kernels, compact, completely continuous II: 67Ч72
Kernels, compact, finite rank II: 65Ч67 72
KroneckerТs algorithm I: 66 II:
L-stability II: 151
Laguerre polynomials I: 186
LaguerreТs method II: 165
Lanczos biorthogonal method II: 76
Lanczos T-method II: 138Ч145
Laplace transform, inversion of II: 153Ч155
Lattice-cutoff field theory II: 176Ч178
LaurentТs theorem I: 49
Le Roy function II: 32
Lemniscates I: 274Ч284
Lippman Ч Schwinger equation II: 82Ч83 113
Logarithmic capacity I: 283
Markov problem II: 137
Matrix Pade approximants II: 50Ч56
Measure, convergence in I: 263
Meromorphic functions, convergence of sequences of I: 259
Mittag Ч Leffler star I: 50
Moment bounds I: 186
Moment method II: 46
Moment problems I: 178Ч179
Moment, definition of Hamburger I: 208 222
Moment, definition of Hausdorff I: 195
Moment, definition of Stieltjes I: 158
Moments, bounds for I: 186 II:
Multi-index I: 239
Multipoint Pade approximation I: 254 II:
Multipole I: 49
Multivariable approximants II: 40Ч50
N-point Pade approximants II: 1Ч31
Natural logarithm I: 140 144
Newton interpolating polynomials II: 2Ч3
Newton Ч Pade approximants II: 1Ч31
NuttallТs compact form I: 16
NuttallТs theorem I: 269
Orthogonal polynomials I: 82Ч86 209Ч210 255Ч256
Osculatory rational interpolation II: 1Ч31
P-fraction I: 130Ч131
Pade approximant I: 1Ч288 II:
Pade denominator, definition of I: 4
Pade equations I: 2Ч3
Pade numerator, definition of I: 6
Pade table I: 7Ч8 27Ч31
Pade Ч Tchebycheff approximants II: 56Ч62
Pade-Borel approximation II: 29Ч30
Pade-Fourier approximants II: 62Ч63
Pade-Frobenius definition I: 20 22
Pade-Legendre series II: 21Ч29
Parabola theorem for continued fractions I: 150
Parabola theorem of Saff and Varga I: 229Ч232
Paradiagonal sequences I: 236
Peres model II: 167
PerronТs counterexample I: 238
Pion Ч Pion scattering II: 172Ч176
Poles and zeros of Pade approximants I: 31 49Ч59 96Ч102 126 166 263
Poles and zeros of Pade approximants for Hamburger functions I: 209 227
Poles and zeros of Pade approximants for Stieltjes functions I: 186 193
Poloids II: 175
Polya frequency series I: 227Ч235
PommerenkeТs theorem I: 271
Potential scattering II: 79Ч126
Projection techniques II: 72Ч79
Prong method II: 43Ч44
PrymТs function I: 140 147
Q. D. algorithm I: 99 125Ч126
Q. D. algorithm for T-fractions II: 20
Q. D. algorithm, generalized II: 13Ч14
Q. D. Table I: 99 125Ч126
Quadratic approximants II: 36Ч37 49
Quadrature II: 127Ч132
Quantum theory, connection with II: 79Ч126
Quasi-analytic functions I: 51
Ratio method II: 33
Rational approximation II: 155Ч162
Rational interpolation II: 1Ч31
Ray sequences I: 191
Real J-fractions I: 128 225
Real symmetric functions I: 160Ч161 180
Regular C-fraction I: 127
Reliability I: 63 132 II:
Rhombus rule I: 77 81
Riccati equation, Pade approximants for II: 162Ч165
Riemann sphere I: 257
Root problem I: 96Ч102
RoucheТs Theorem I: 279
RungeТs theorem II: 158Ч159
S-fraction I: 127Ч128 165 206
S-matrix, partial wave II: 89 91
Saffs theorem I: 254
Scattering theory, quantum mechanical II: 80Ч92
SchwarzТs lemma I: 189 192
Sectorial theorem of Saff and Varga I: 229
SeidelТs theorem I: 148Ч150
Sequence, acceleration of convergence of I: 16Ч17 69Ч90
Sequence, column I: 30
Sequence, diagonal I: 17 32 35
Sequence, paradiagonal I: 30
Sequence, row I: 30
Series analysis I: 55Ч57 59Ч61 II:
Series, acceleration of convergence of I: 16Ч17 69Ч90
Shafer approximants II: 36Ч37
Single-sign potentials II: 106Ч114
Singular potentials II: 120Ч126
Spherical convergence I: 256Ч263
Star Identity I: 23
Stieltjes function I: 158 208
Stieltjes function, definition of I: 158 221
Stieltjes function, numerical calculation of I: 64
Stieltjes inversion formula I: 221
Stieltjes series I: 158 208
Stieltjes series, definition of I: 158 221
Stieltjes series, example of I: 161
Stieltjes series, inequalities for Pade approximants of I: 170
Stieltjes series, S-fraction for I: 165
Sturm sequence I: 167
SylvesterТs theorem I: 23 167
T-fractions I: 138 II:
T-matrix II: 81Ч82 103 172Ч176
T-matrix, partial wave II: 89
T-matrix, Toeplitz matrix I: 67
T-matrix, Totally monotone sequence I: 195
T-matrix, Totally positive series I: 228
T-matrix, TrudiТs theorem I: 42
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



 -Algorithm
-Algorithm  -Algorithm
-Algorithm 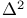 method
method  -dimensional
-dimensional 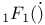 , Pade approximants of
, Pade approximants of 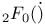 , Pade approximants of
, Pade approximants of 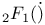 , Pade approximants of
, Pade approximants of