|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Dimca A. Ч Singularities and Topology of Hypersurfaces |
|
|
 |
| ѕредметный указатель |
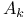 -singularities 13 59Ч60 95 203 222 226 -singularities 13 59Ч60 95 203 222 226
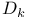 -singularities 13 59Ч60 222 226 -singularities 13 59Ч60 222 226
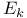 -singularities 13 59Ч60 222 226 -singularities 13 59Ч60 222 226
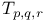 -singularities 13 60Ч62 207 223 245 -singularities 13 60Ч62 207 223 245
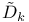 -binary dihedral group 111 -binary dihedral group 111
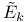 -singularities 13 63Ч64 203 222Ч223 -singularities 13 63Ч64 203 222Ч223
(Hyper)plane section 15 25Ч26 133Ч135 137
Adjunction formula 141
Affine hypersurface 19Ч22 28 103 174Ч176 244
Affine variety 26 28 182 233
Alexander ideal 38
Alexander invariant 35Ч36
Alexander matrix 38 92
Alexander polynomial of a hypersurface 106Ч110 206Ч216
Alexander polynomial of a knot 38Ч40 44
Alexander polynomial, local 206Ч207
Borromean rings 41
Braid groups 113Ч115
Briancon Ч Speder example 12
Brieskorn Ч Pham singularities 94Ч99 105Ч106 211
Casson invariant 98Ч99
Cayley Ч Bacharach theorem 212
Chern classes 151Ч152
Compact polyhedron 27 75
Complete intersection, locally 25
Complete intersection, projective 142Ч176
Complete intersection, singularity 24Ч25 76 80Ч81 90
Conic structure 23 163
Connectivity 76 79
Contraction of a resolution graph 56 60 62
Contraction with a vector field 179Ч180
Covering, cyclic 34Ч35 90 234
Covering, universal 28 112
Cubic curve 194 216
Cubic surfaces 165Ч166
Curve singularity 41Ч49 100 117Ч120 125 220
Cusp singularities 13 60Ч62 207 223 245
CW-complex 27 139
Cylindric structure 26 75 157
de Rham Ч Koszul complex 190
Defect of a linear system 207Ч208
Degeneration 121 126 128 138 214Ч215
Differential forms 177Ч180
Discriminant, form 225Ч226
Discriminant, group 220 226
Discriminant, hypersurface 81 132
Distinguished basis 83
Dolgachev numbers 63 224
Du Val singularities 13 59Ч60 222 226
Dual hypersurface 14 131
Durfee conjecture 159
Dynkin diagram 60 221Ч224
EhresmannТs Fibration Theorem 15
Eilenberg Ч MacLane space 32 115 146
Equivalent germs 2
Essential singularity 205 207
Euler vector field 179 181
Exceptional singularities 13 62Ч63 223Ч224
Filtration, Hodge 185Ч188 202 217 240
Filtration, polar 184Ч188 202 217
Filtration, weight 241 245
Fitting ideal 38 44
Foliations of a sphere 98
Free product of groups 56 111 134
Fundamental group 27 105 116
Fundamental group of a hypersurface complement 26 80 101Ч138
Fundamental group of a knot complement 32Ч40
Fundamental group of a link 53Ч58
Fundamental group, local 2 103Ч104
Gabnelov numbers 63 224
Graph 94 113
Graph of a resolution 50 60 218 229 245
Grothendieck residue 49
Group, isotropic (subgroup) 225
Group, isotropy 197
Group, of a knot 32
Group, reflection 57
Group, small 57Ч58
Gysin sequence 46 77 198
Heisenberg group 64
Hirzebruch Index Theorem 153
Hirzebruch Ч Jung singularities 58 231
Hodge numbers 236 240Ч241 246
Hodge structures 240Ч247
Homology manifold 164 232 243
Hopf bundle 32 139 142
Hyperbolic singularities 13 60Ч62 207 223 245
Hypersurface, nodal 17Ч19 208Ч210 218
Hypersurface, quadratic 194
Hypersurface, smooth projective 15 109 152
INDEX 98 221 237 240
Inflectional tangent 120 127 186
Intersection, cohomology 217
Intersection, form 37 52 86 89
Intersection, matrix 52 83
Intersection, number 45 89 100
Join 27 87Ч88 135Ч137
K3 surface 160 236
Kahler manifold 239
Knot 29
| Knot, (p, q) torus 31 33Ч35 43
Knot, algebraic 42
Knot, fibered 39
Knot, trefoil 31 40
Knot, trivial 30 33
Lattice 219
Lattice, even/odd 154Ч155 219
Lattice, morphism of 220
Lattice, nondegenerate 219
Lattice, reduced 220
Lattice, skew-symmetric 220
Lattice, unimodular 219
Lefschetz number 75 108
Lefschetz Theorem 25
Lens space 59
Line configuration 212Ч213
Link 23 29 66 245
Link at infinity 28 175
Link, algebraic 42
Link, fibered 39
Link, trivial 30 41
Linking form 227Ч228
Linking number 33 45
Milnor number 10 78 162Ч163
Milnor number,  -constant 10 12 -constant 10 12
Milnor number,  -determinacy 125 -determinacy 125
Milnor number,  -equivalent 10 -equivalent 10
Milnor number, 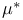 -constant 12 -constant 12
Milnor number, 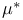 -invariant 11Ч12 -invariant 11Ч12
Milnor number, global 21
Milnor, algebra 193 236 244
Milnor, fiber 68Ч75 82 133 163 237
Milnor, lattice 83 89Ч90 157Ч158 161 167 170Ч172 220 227Ч229
Monodromy, homeomorphism 40 73Ч74
Monodromy, operator 40 44 73Ч75 86
Monodromy, relation 119Ч120 127
Morsification 82
N-equivalence 25
Normal bundle 141 152 155
Normal crossing singularity 79 105
Normal singularity 50 55 104
Parallelizable manifold 75 97
Picard Ч Lefschetz transformation 85
Pinch point 4 11 24
Pliicker formula 14
Poincare icosahedral sphere 60
Poincare series 65
Poincare Ч Leray residue 46Ч47 192Ч193 200
Pole (order of the) 184
Pontrjagin classes 153
Presentation 38 111 127
Presentation, matrix 38Ч40
Primitive (co)homology 146Ч147 234
Primitive embedding 90 224 227
Projective cone 169Ч170
Projective space 139Ч142 230Ч232
Projective space, (co)homology 109 145 147Ч148 167
Quartic curves 126 129Ч133
Quasismooth 232
Quotient singularities 57Ч60 231Ч233
Rational double points 13 59Ч60 222 226
Resolution of singularities 50 52 59Ч63 66Ч67 218 228 243 245
Resultant hypersurface 80
Seifert, invariants 65
Seifert, matrix 36Ч38 85Ч86
Seifert, surface 34
Semiweighted homogeneous singularity 12 74 125 204
Signature 221 244
Simple-elliptic singularities 13 63Ч64 203 222Ч223
Smith Theory 173Ч174
Smith Ч Gysin sequence 231
Sphere, exotic 97Ч98
Sphere, homology 53 60 93Ч97
Stabilization of singularities 89
Stein variety 26 69 182
Stratification 3
Stratification, Samuel 4
Stratification, topologically locally trivial 8
Stratification, Whitney (regular) 4 6Ч7 17 135
Stratum 3
Surface singularity 49Ч67 245
Thom Ч Sebastiani construction 27 86Ч90 135
ThornТs First Isotopy Lemma 16
Tjurina number 81
Transversal singularity 197
Triangle singularities 13 62Ч63 223Ч224
Unimodular matrix/lattice 37 53 164
Vanishing cycle 83
Veronese embedding 15
Veronese variety 15
Wang sequence 61 73
Weight 64
Weighted homogeneous, projective space 105 230Ч237
Weighted homogeneous, projective variety 230Ч237
Weighted homogeneous, singularity 64Ч67 71Ч74 79 87 202Ч204 236 243Ч244
Whitney regularity 3 12
Whitney umbrella 4 11 24
Zariski conjecture 2
Zariski sextic curves 18 134Ч138 210Ч211
УTubularФ neighborhood 148Ч151
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



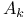 -singularities
-singularities 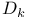 -singularities
-singularities 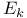 -singularities
-singularities 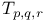 -singularities
-singularities 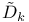 -binary dihedral group
-binary dihedral group 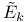 -singularities
-singularities  -constant
-constant 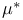 -constant
-constant