Авторизация
Поиск по указателям
Bichteler K. — Integration - a functional approach
Обсудите книгу на научном форуме Нашли опечатку?
Название: Integration - a functional approachАвтор: Bichteler K. Аннотация: This book covers Lebesgue integration and its generalizations from Daniell's point of view, modified by the use of seminorms. Integrating functions rather than measuring sets is posited as the main purpose of measure theory.
Язык: Рубрика: Математика /Анализ /Продвинутый анализ /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1998Количество страниц: 193Добавлена в каталог: 02.04.2005Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Integral of Lebesgue 64 Integral, elementary 33 35 Integral, extended 25 57 65 Integral, positive elementary 35 Integral, product of elementary 123 Integrand, elementary 35 Integrand, elementary Banach space valued 77 Interpolation 99 133 Intersection 4 Inverse 4 Isometric 116 120 122 Iterated integration 124 Iterated upper integral 125 Jensen's inequality 154 JORDAN 29 Jordan mean 22 46 57 Laplace transform 14 Largely 71 Largely from 68 Largely uniform convergence 69 72 Lattice 107 Lattice algebra 6 Lattice ring 6 7 11 14 18 23 35 37 39 40 47 54 56 65 86 89 97 99 125 134 138 141 147 149 151 171 Lattice ring, generated by functions 83 Lattice, generated by functions 83 Least upper bound 106 Lebesgue 93 97 Lebesgue, inner measure 94 Lebesgue, integrable 59 69 Lebesgue, integral 64 Lebesgue, integral, elementary 35 Lebesgue, measurable 70 Lebesgue, measure 19 49 64 Lebesgue, negligible 26 49 Less than 3 Limit inferior 3 Limit superior 3 Limit, uniform 6 10 Linear functional on a real vector space 110 Linear functional, positive 114 Linear operator 105 Linear space 6 Linearly generate 19 Lipschitz function 56 Little 28 Littlewood's Principles 67 68 Localizable 109 Locally compact 37 Locally integrable 149 Lorentz space 132 Lower semicontinuous 47 88 Lower, envelope, integrable 60 Majorize 19 Majorize by a mean 64 78 90 125 135 Majorize by a seminorm 29 32 46 48 Majorize by a step function 2 Majorize by an integrable function 60 Majorize, the elementary integral 22 32 46 57 64 78 90 125 135 Majorize, the integral 19 22 23 48 Maximal mean 74 90 99 102 Maximal operator of Hardy — Littlewood 155 Maximum of elements in an ordered set 106 MCT 104 Mean 32 46 Mean closure 52 Mean on a ring of functions 46 Mean, 62 Mean, (totally) finite 62 Mean, canonical 90 Mean, continuous along arbitrary increasing sequences 91 99 Mean, convergence 45 Mean, Daniell 45 91 92 Mean, Daniell — Stone 48 56 78 92 Mean, maximal 74 90 99 102 Mean, order-continuous 48 88 Mean, solidity of a 135 Mean, strictly increasing 92 Mean-convergence 22 Mean-dense 56 74 Measurability 67 70 Measurable 67 70 97 Measurable for 70 Measurable function 70 97 Measurable function, simple 79 Measurable on a 87 Measurable set 78 97 Measurable space 90 Measurable, function on a set 70 Measurable, Lebesgue 70 Measure of finite variation 139 Measure on a ring of sets 38 Measure zero 27 Measure, 62 129 Measure, image of a 153 Measure, inner 94 Measure, outer 64 Measure, positive, on a ring of sets 38 Measure, product of 124 Measure, signed 135 Measure, totally finite 62 Metric 4 Metric space 4 15 47 71 73 88 Minimal representation 19 Minimum of elements in an ordered set 106 Minkowski functional 115 Minkowski's inequality 101 119 120 Monotone class 89 Monotone Convergence Theorem 104 Natural number 3 Negative 3 Negative part 108 Negative, strictly (<0) 3 Negative-homogeneity 20 Negligible 49 Norm 10 27 Norm of a linear functional 110 Norm, uniform 10 Normal homomorphism of vector lattices 148 Normed vector lattice 107 Normed vector space 27 Numerical function 4 Observable 41 Operator of strong type 133 Operator of weak type 133 Operator, linear 105 Order 106 Order bound 106 Order complete 107 Order cone 108 142 Order interval 56 Order on 106 Order preserving map 116 Order, quotient, for vector lattices 148 Order-completeness 107 Order-completeness of 109 Order-completeness of 110 Order-completeness of the dual of a vector lattice 116 Order-completeness, non- of 109 Order-continuous, elementary integral 37 138 Order-continuous, mean 48 88 Orthogonal 121 Orthogonal elements of a vector lattice 145 Outer measure 49 64 93 Outer regularity 65 p-integrable 103 p-mean 100 p-mean, convergence 100 p-Norm 33 100 Pairing 116 Parseval's identity 122 Partition 18 Permanence properties 23 67 79 Permanence properties of 104 Permanence properties of Baire and Borel functions 83 Permanence properties of integrable functions 52 65 Permanence properties of integrable sets 61 Permanence properties of measurability 72 76 77 97 129 Permanence properties of negligibility 49 Permanence properties of the integral 135 Permanence properties of the Riemann integral 23 29 Perpendicular 121 Piecewise continuous 163 Pointed cone 108 Polarization 12 Positive 120 Positive 3 Positive bilinear form 120 Positive bounded linear functional 114 Positive elementary integral 18 29 35 Positive measure on a ring of sets 38 Positive part 107 Positive Radon measure 37 Positive, strictly (>0) 3 Positive-homogeneous 19 Power set 164 probability 41 153 Product of elementary integrals 123 Product of measures on rings of sets 124 Product of Radon measures 125 Product of rings of sets 124 Pseudometric 15 Pseudometric of convergence in measure 82 Quotient norm 28 106 Quotient order for vector lattices 148 Radon measure 138 Radon measure, positive 37 138 Radon measure, product of 125 Radon — Nikodym derivative 152 153 Rational number 3 Real Hilbert space 121 Real line 3 Real numbers 3 rectangle 124 Reflexive 99 114 Reflexive, relation 106 Regularity inner and outer 65 Relation, antisymmetric 106 Relation, reflexive 106 Relation, transitive 106 Relative complement 4 Riemann 1 17 Riemann integrable on (a,b] 26 Riemann, integrable 1 17 20 21 22 24 25 26 162 Riemann, integral 1 17 23 37 Riemann, lower sum 17 Riemann, squeeze 1 93 97 Riemann, upper sum 17 Riesz representation theorem 64 Riesz space 107 Riesz space of functions 6 Right translate 65 Right-continuity of a distribution function 141 Right-continuous version of a function 141 Ring of functions 6 7 11 13 14 16 46 52 57 68 71 86 90 123 Ring of sets 19 38 40 61 78 85 93 95 96 98 124 137 147 Ring of sets, generated 38 Ring, generated by functions 83 Self-adjoint 134 Self-confined 8 29; Self-confining 8 14 16 18 56 Seminorm 2 10 27 Seminorm solid 29 32 46 48 49 54 68 87 92 102 103 107 115 Seminorm, the, of an inner product 120 Seminormed vector lattice 107 Seminormed vector space 27 Separable 28 60 88 105 122 Separating the points 12 16 73 162 Sequential closure or span 84 Sequentially closed family of functions 84 Set function 93 Set, difference of 4 Set, identified with indicator function 5 Set, integrable 61 Set, measurable 78 97 Signed elementary integral 134 Signed measure 135 Simple 87 Simple function 40 Simple integrable function 61 64 97 Simple measurable function 79 Solid, seminorm 29 32 46 48 49 54 68 87 92 102 103 107 115 Solid, seminorm on an ordered vector space 107 Solid, subset of a vector lattice 145 Solidity 11 22 29 32 46 48 54 68 87 92 102 103 107 146 Solidity of a mean 135 SQUEEZE 1 2 20 93 97 Step function 38 40 Step function on the line 18 Strictly increasing 109 Strictly increasing mean 92 102 Strictly, positive or negative 3 Strong type operator 133 Subadditivity 11 19 22 27 54 120 133 165 172 173 Subadditivity, countable 33 44 46 48 66 68 72 90 94 102 103 126 Submultiplicative 105 Summable sequence in a seminormed space 28 Superadditivity 20 45 94 136 173 Superadditivity, countable 47 Support 7 Support of 78 Support of a function 61 65 125 138 156 Support, function of compact 7 26 37 47 Surjection 4 Symmetric bilinear form 120 Symmetric, difference 6 19 Tensor product of function spaces 8 Totally finite, elementary integral 62 Totally finite, mean 62 Totally finite, measure 62 Transitive relation 106 Translation invariance 60 105 Triangle inequality 2 15 27 168 Triangle inequality on a vector lattice 144 Trigonometric polynomial 31 Uniform closure 10 13 15 165 Uniform convergence on arbitrarily large sets 72 Uniform convergence, largely 69 72 Uniform distance 10 Uniform integrability 56 57 Uniform limit 6 10 Uniform norm 10 Uniform, dominated convergence 25 Uniformity 15 Uniformly continuous 15 69; Uniformly continuous, largely 71 union 4 Union-and-down-procedure 128 Upper integral 42 Upper integral, iterated 125 Upper Riemann integral 1 19 Upper Riemann sum 17 Upper, Envelope, 91 131 172 Upper, envelope, integrable 60 Upper, integral, Daniell — Stone 48 Variation of an element in a vector lattice 107 Variation of an elementary integral 135 Variation, finite 135 Variation, function of finite 140 Vector lattice 107 108 123 142 Vector lattice of functions 6 128
Реклама
 |
|
О проекте
|
|
О проекте



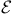 -uniformly continuous
-uniformly continuous 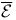

 -spaces
-spaces  -finite
-finite 

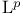



 -measurable function
-measurable function  on an integrable set
on an integrable set