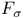|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Rudin W. — Real and Complex Analysis |
|
|
 |
| Предметный указатель |
Inner product 75
Inner regular set 47
integral 19 24 130 202
Integration 19
Integration by parts 176 226 239
Integration of derivative 166 168
Integration over measurable set 20
Integration over path 202
Integration with respect to complex measure 130
Interior 254
Interpolation 246 298
Intersection 6
interval 7
Invariant subspace 190 341
Inverse function theorem 173
Inverse image 7
Inverse mapping 7 217
inversion 269
Inversion formula 182
Inversion theorem 186 187 189
Invertible element 352
Invertible operator 171
Isolated singularity 211
Isometry 84 187 363 365
Isomorphism 86 187 363 365
Iterated integral 141 143
Jacobian 174 221
Jensen’s formula 300
Jensen’s Inequality 61 300
Jordan curve 282
Jordan decomposition 120 127 340
Jordan, C 5
Kahane, J. P. 398
Kakutani, S. 398
Kernel 357
Koebe mapping 287
Laplace equation 223
Laplacian 196 223
Laurent series 266
Lebesgue decomposition 122 155
Lebesgue integrable function 24 52 69
Lebesgue integral 19
Lebesgue measurable set 50
Lebesgue measure 50
Lebesgue set 158
Lebesgue, H. J. 5 21 26 165 393 395
Left-continuous function 161 179
Left-hand limit 161
Length 176 203
Limit, pointwise 14
Limit, pointwise, in mean 66
Limit, pointwise, in measure 73
Limit, pointwise, of measurable functions 14
linear combination 81
Linear fractional transformation 269 288
Linear independence 81
Linearly ordered set 87
Liouville’s theorem 213 274 354
Lipschitz condition 114
Locally compact space 36
Locally integrable function 196 237
Logarithm 221 263
Lowdenslager, D. 343 398
Lower derivative 153
Lower half plane 230
Lower limit 14
Lower semicontinuous function 37
Lusin’s theorem 53
Mandelbrojt, S. 399
Mapping 7
Mapping, continuous 8
mapping, one-to-one 7
Mapping, open 99 173 216
Maximal ideal 357 360
Maximal orthonormal set 85
Maximal subalgebra 361
Maximality theorem 392
Maximum modulus theorem 111 213 249 258 357
Mean value property 230 237
Measurable function 8 28 150 393
Measurable set 8 50
Measurable space 8
Measure 16
Measure space 16
Measure,  -finite 47 -finite 47
Measure, absolutely continuous 121 335
Measure, Borel 47
Measure, complete 27
Measure, complex 16 131
Measure, continuous 149
Measure, counting 17
Measure, discrete 149
Measure, Lebesgue 50
Measure, positive 16
Measure, real 16
Measure, regular 47 131
Measure, representing 110 394
Measure, signed 120
Measure, singular 121
Measure, translation invariant 50
Mergelyan’s theorem 386 399
Meromorphic function 260 296
Metric 9
Metric density 177
Metric space 9
Minkowski’s inequality 62 65
Mirkil, H. 399
Mittag — Leffler theorem 296 308 309
Modular function 320
Modular group 320
Monotone class 136
Monotone Convergence Theorem 21
Monotone function 176
Monotonicity 17 42
Morera’s theorem 209
Moschovakis, Y. N. 397
Multiplication operator 116 199 341 364
Multiplicative inequality 351
Multiplicative linear functional 360
Multiplicity function 179
Multiplicity of a zero 216 293
Muntz — Szasz theorem 305 309
Natural boundary 313 315 323
Negative part 15
Negative variation 120
Neighborhood 9 35
Neumann, J. von 123 394
Nevanlinna, R. 303
Nonmeasurable set 52 143 395
Nonsingular operator 171
Norm 64 75 95 169 330
Norm-preserving extension 107
Normal family 271
Normalized function 81 161
Normed algebra 351
Normed linear space 95
Nowhere dense 98
Nowhere differentiable function 115
Null space 357
Null-homotopic curve 261
One-parameter family 261 318
One-to-one mapping 7
Onto 7
Open ball 9
Open cover 35
Open mapping theorem 99 216 267 396
Open set 8
Opposite path 203
Orbit 308
Order of entire function 310
| Order of pole 211
Order of zero 210
Ordinal 58
Ordinate set 148 395
Oriented interval 203
Orthogonal projection 79 190 343
Orthogonality 35 78
Orthogonality relations 81
Orthonormal basis 85
Orthonormal Bet 81
Ostrowski, A. 314
Outer factor 338
Outer function 336
Outer measure 393
Outer regular set 47
Overconvergence 314
Paley — Wiener theorems 368 370
Parallelogram law 79
Parameter interval 202
Parseval’s identity 85 92 189 213 333
Partial derivative 222
Partial fractions 253
Partial product 290
Partial sum of Fourier series 91 101 116 349
Partially ordered set 87
Partition of set 117 133
Partition of unity 40
Path 202
Perfect set 176
Periodic function 2 88 178 267
Perron, O. 167
Phragmen — Lindelof method 243
Picard theorem 324 398
Plancherel theorem 187 368 371
Plancherel transform 187
Point of density 177
Pointwise limit 14
Poisson integral 112 224 228 235 332
Poisson kernel 112 223
Poisson summation formula 197
Polar coordinates 149
Polar representation of measure 126
Pole 211
Polynomial 110 218
Positive linear functional 34 40 109
Positive measure 16
Positive part 15
Positive variation 120
Positively oriented circle 203
Power series 200 209
Pre-image 7
Preservation of angles 268
Prime end 397
Principal part 211
Product measure 140
Projection 79 190 343 349
Punctured disc 198
Quasi-analytic class 374
Quotient algebra 358
Quotient norm 358
Quotient space 358
Radial limit 226 232 235 304 347
Radical 365
Radius of convergence 200
Radon — Nikodym derivative 122 155
Radon — Nikodym theorem 122 126 156
RANGE 7
Rational function 219 253 284
Real line 7
Real measure 16
Real-linear functional 105
rectangle 136
Reflection principle 230 271 284 396
Region 198
Regular Borel measure 47 131
Regular point 312
Removable set 326
Removable singularity 211
Representable by power series 200
Representation theorems 40 80 128 131
Representing measure 110 394
Residue 215
Residue theorem 215 259 260
Resolvent 365
Restriction 20 109
Riemann integral 5 34 51
Riemann mapping theorem 264 273 287
Riemann sphere 252
Riemann — Lebesgue lemma 103
Riess, M. 328 335 345 396
Riesz representation theorem 34 40 131 234 256 393
Riesz, F. 34 328 335 393 396
Riesz-Fischer theorem 85 91 92 333
Right-hand derivative 395
Right-hand limit 161
Root test 200
Rotation 269
Rotation invariance 178
Rouche’s Theorem 218 266 275
Rubel, L. A. 397
Runge’s theorem 255 258 397
Saks, S. 393
scalar 33
Scalar product 75
Schwartz, J. T. 394
Schwarz inequality 49 75
Schwarz lemma 240
Schwarz reflection principle 230
Schwarz, H. A. 396
Second category 98
Section 136
Segment 7
Separable space 93
Set 6
Set, 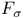 12 12
Set,  12 12
Set, Borel 12
Set, closed 12 35
Set, compact 35
Set, connected 198
Set, convex 78
Set, dense 56
Set, elementary 136
Set, empty 6
Set, inner regular 47
Set, measurable 8 50
Set, nonmeasurable 52 143 395
Set, open 8
Set, outer regular 47
Set, partially ordered 87
Set, perfect 176
Set, strictly convex 113
Set, totally disconnected 56
Set, totally ordered 87
Shift operator 341
Sierpinski, W. 143 395
Signed measure 120
Simple boundary point 279
Simple function 15 67
Simply connected 262 319 325
Sine 2 251
Singer, I. M. 394 399
Singular function 168
Singular measure 121 337 344
Singular point 312
Snow, D. O. 395
Space, Banach 95 331
Space, compact 35
Space, complete metric 66 76 95
Space, dual 108 128 238
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -finite
-finite