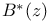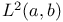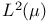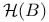|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| de Branges L., Rovnyak J. — Square summable power series |
|
|
 |
| Предметный указатель |
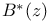 47 47
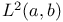 91 91
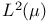 88—91 88—91
 4—5 38 42 4—5 38 42
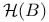 22—24 33 22—24 33
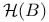 , characterization of spaces 38—39 , characterization of spaces 38—39
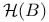 , decomposition of spaces 29 32 , decomposition of spaces 29 32
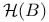 , equality of spaces 33 , equality of spaces 33
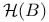 , finite dimensional spaces 29 51 53—54 , finite dimensional spaces 29 51 53—54
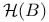 , inclusions 29—30 32—33 , inclusions 29—30 32—33
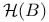 , relation to , relation to 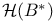 47—49 47—49
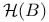 , relation to , relation to  23 29 23 29
 11 11
Absolute value 1
Adjoint transformation 34 35 38 39 42
Adjoint transformation of difference-quotient transformation 36 37 39 46 47
Approximation by Blaschke products 51
Approximation by Borel measurable functions 86
Approximation by finite dimensional spaces 53
Approximation by polynomials 19
Aronszajn, N. 71
B-norm 22
Bessel’s inequality 7
Beurling, A. 12 34
Beurling’s factorization 97
Blaschke product 17 33 51 54
Borel measurable function 86—87
Borel measurable function, conjugate of 86
Borel measurable function, limits of 86
Borel measure 82—86
Borel measure and nondecreasing functions 82
Borel set 81
Bound of a transformation 47—48
Boundary value function 91—95 98
Bounded function 17 18—19 22 28 29 31—33 70
Bounded type 95—99
Bounded type and non-negative real part 96
Bounded type and square summable power series 96 98
Canonical model 34—35 42
Cantor diagonal procedure 53 80 81
Caratheodory condition 84
Cauchy sequence of complex numbers 1
Cauchy sequence of vectors 8
Cauchy’s Theorem 63—67
Change of measure theorem 79
Characterization of  38 38
Characterization of difference-quotient transformation 34—35
Characterization of functions of bounded type 96
Characterization of range of multiplication by B(z) 29
Characterization of spaces  39 39
Closed curve 62—63
Closed ideal 10—14 33
Closed ideal, examples 11 15 16 17 33
Closed ideal, generated by a power series 33 97 98
Closed set 8
Closed span 10
Commuting transformations 28 55—56
Completeness of  8 8
Completeness of  24 24
Completeness of complex numbers 2
Completeness of inner product spaces 8
Completeness of Lebesgue spaces 88
complex numbers 1
Conjugate of a Borel measurable function 86
Conjugate of a complex number 1
Construction of closed ideals 10—11
Construction of measures 83
Continuity of function values 14 28
Continuity of inner product 10
Continuity of length of a curve 59 63
Continuous linear functional 10
Continuous transformation 34
Contour integral 58
Convergent power series 14 18—19
Convergent sequence 1
Convex region 67
Convex set 8
Countable number of discontinuities 81
Curve 57
Decomposition of open sets 82
Decomposition of spaces 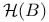 29 32 29 32
Density of continuous functions in 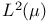 91 91
Difference quotient 14 29
Difference quotient and minimal decompositions 36 44—46
Difference quotient in 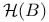 29 39 43 29 39 43
Difference quotient, identity 38—39 42—43 46
Difference-quotient transformation 34—39 45—47
Differentiability 14 57 59 67 68 70
Differentiable function 14 57
Differentiable function as derivative 67
Discontinuities of nondecreasing function 81
Disjoint sequence of sets 82
Double orthogonal complement 10
Equivalence classes of functions 88
Estimate of function values 97—99
Existence of factors 53
Existence of integral 58
Existence of subsequence 53 80
Existence of subspaces 53
Exponential function 3 52 55
Factorization 17 18 30—31 53 97—99
Factorization theorem 53
Factors of B(z) 17 18 29 30
Fatou’s theorem 91
Finite dimensional space 51 54
Formal convergence 19
Formal power series 2—3
Function values 14 28
Function values, bounded by one 17 18 70
Function values, estimate of 97—99
Fundamental theorem of algebra 18 70
Fundamental theorem of the calculus 59
Goursat, E. 63
Helly selection principle 80
Helly, E. 80
Herglotz, G. 79
Herglotz’s theorem 80
Hilbert space 8
Hilbert space of power series 38 39
Ideal 10
Ideal theorem 12
Ideal, closed 11—14 33
Ideal, examples of closed ideals 11 15 16 17 33
| Identity for difference quotients 38—39 42—43 46
Inclusions of spaces 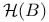 29 30 32—33 29 30 32—33
Indeterminate 57
Infinite products 15
Infinite products, expressed in terms of norms 7 24
Infinite products, inner product 3 4
integral 58 79
Integral and sums 79
Integral over a curve 58—67
Integral, Lebesgue 87—91
Integral, Stieltjes 79 91
Integral, Stieltjes and Lebesgue 91
Interval of parametrization 57
Invariant subspace 33
Isometric inclusion 32
Isometric multiplication 11 32 33
Isometric multiplication and factors 33
Isometric substitution 49 54
Isometric transformation 34 47
Jensen’s Inequality 96—97
Kernel of a linear functional 10
Laguerre polynomial 3
Landau, E. 1
Lebesgue and Stieltjes integrals 91
Lebesgue integral 87—91
Lebesgue space 88
Lebesgue, H. 83
Left and right limits 59 64
Limits of Borel measurable functions 86
Linear functional 10
Linear transformation 2
Linearity 4
Logarithm 96
Maximum principle 17 29 68—70
Measurable function 86—87
Measure 82—86
Measure and nondecreasing function 82 83
Measure, change of measure theorem 79
Mesh of a partition 58
Minima of modulus 70
Minimal decomposition 26—29 31—32 36 44—46
Minimal decomposition and difference quotients 36 44 45
Multiplication by B(z) 11 18 28 29 33 54—55
Multiplication by z 13—14 38 43 45
Nevanlinna, R. 95 98—99
Nevanlinna’s estimate 98
Nevanlinna’s factorization 99
Non-negative real part 80
Non-negative real part and bounded type 96
Nondecreasing function 79 80 82 83 89
Norm 5
Norm of limit 19 91
One-dimensional range 34 37 39 42
Orthogonal complement 10
Orthogonal complement of ideal 23
Orthogonal sequence 7
Orthogonality 7
Outer measure 82—86
Parallelogram law 5 6—7 23
PARAMETER 57
Partial isometry 39 56
Partition 57
Perpendicular 7
Perpendicular and shortest distance 9
Poisson formula 76
Poisson kernel 92
Poisson representation 79
Polynomial 19
Polynomial and Blaschke products 33
Positive-definiteness 70
Positivity 4
Power series see “Formal power series”
Power series, convergent power series 14 18—19
Power series, square summable power series 4
Powers tending to zero 34—35
Products of Borel measurable functions 86
Products of functions of bounded type 96
Products of power series 3
Projection 9
R(w) 36 46
Rational function and Blaschke product 33
Rectangular region 63
Refinement of a partition 58
Region 57
Representation of continuous linear functionals 10
Representation of differentiable function as power series 70
Riesz — Fischer theorem 88—91
Riesz, F., and Sz.-Nagy, B. 88
Rovnyak, J. 12
Schwarz inequality 5—6
Schwarz inequality, equality in 6 12
Schwarz’s lemma 70
Sequence of finite Blaschke products 51
Sequence of nondecreasing functions 80
Sequence of polynomials 19
Sequence of spaces 53
Series see “Formal power series”
Series and functions 14 57
Sets of measure zero 88
Shortest distance 9
Soap bubble theorem 77
Space of dimension zero or one 53
span 9
Square integrable function 87—88
Square summable power series 4
Square summable power series and bounded type 96 98
Stieltjes and Lebesgue integrals 91
Stieltjes integral 79
Subadditivity of outer measure 82—83
Substitution theory 49—51 54—55
Sums of Borel measurable functions 86
Sums of functions of bounded type 96
Sums of squares bounded by one 22
Symmetry 4
Transformations 2 33—36 42
Transformations, commuting 28 55—56
Triangle inequality 6
Uniqueness of shortest distance 9
Unitary equivalence 34 42 47
Variable 57
Vector space 2
Vector space with inner product 4
Walsh, J. L. 15
zeros 17—18
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте