|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hayman W.K. — Multivalent Functions |
|
|
 |
| Предметный указатель |
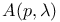 , , 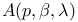 73 73
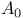 38 38
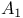 , , 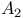 84 84
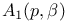 71 71
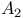 1 162 1 162
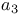 215 215
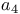 , , 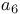 230 230
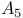 161 230 161 230
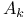 243 243
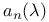 221 247 221 247
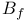 200 200
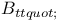 208 208
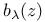 26 26
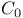 61 61
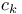 , , 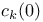 , , 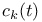 237 237
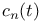 216 216
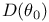 61 61
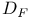 128 128
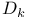 243 243
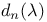 26 243 26 243
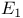 , , 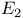 86 86
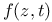 210 210
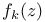 95 161 95 161
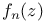 20 20
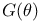 240 240
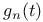 239 242 239 242
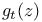 207 207
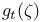 215 237 215 237
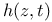 237 237
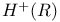 39 39
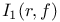 9 9
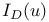 109 109
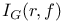 11 11
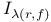 27 67 27 67
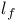 147 147
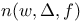 144 144
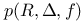 29 29
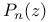 , , 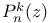 231 231
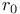 , , 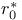 126 126
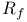 131 131
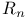 19 19
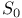 36 36
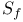 200 200
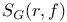 78 78
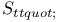 208 208
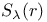 69 69
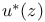 117 117
 9 45 50 150 9 45 50 150
 64 64
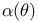 18 18
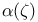 42 42
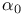 45 45
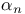 20 20
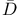 104 104
 55 66 200 209 55 66 200 209
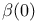 , , 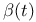 209 209
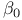 79 79
 20 33 163 20 33 163
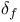 200 200
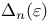 19 19
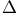 20 20
 82 82
 , the gamma function 26 151 , the gamma function 26 151
 , , 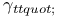 207 207
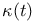 210 210
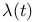 207 207
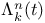 235 235
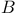 143 143
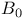 137 137
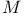 141 141
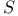 1 1
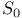 6 149 6 149
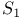 82 197 204 82 197 204
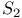 82 82
 33 172 180 33 172 180
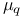 28 28
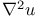 77 107 169 77 107 169
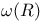 51 51
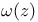 109 243 109 243
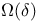 117 117
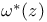 119 119
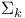 242 242
 209 209
 30 30
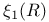 , , 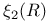 51 51
2-point estimate 176
A(p), 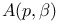 66 66
A(p,b,c) 100
A(p,k,N) 99
A(r,f) 27
Admissible domain 109
Analytic domain 104
Areally mean (a. m.) p-valent 144
Argument of f(z) 224
Argument of f’(z) 226
Asymptotic behaviour 19 60 154 155
Asymptotic behaviour of coefficients 15 64 151 156
Averaging assumptions 19 37 144
B 136
Bieberbach’s conjecture xi 4 230
Bloch functions 143
Bloch’s constant 136
Bloch’s theorem 136
Bounded univalent functions 78
| C, 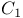 , , 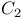 ,... 172 ,... 172
C. A. x 7 103
Circumferentially mean (c. m.) p-valent 144
Coefficients of univalent functions 9 15 247
Coefficients of univalent functions, of mean p-valent functions 65 131
Condenser, capacity of a condenser 109
Connectivity 104
Convex domain 11
Convex function 70
Convex univalent functions 11 12
Correspondence of points under a transformation 200
D, 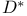 115 115
de Branges’ theorem xi 230
Dense subclass 197
Diameter 199
Dirichlet’s minimum principle 109
Dirichlet’s minimum principle, problem of Dirichlet 108
Distortion theorems 4 28
Domain 104
Functions of maximal growth 16 17 45
Functions of maximal growth with k-fold symmetry 95 159 185
Functions of maximal growth without zeros 145 159
Functions of maximal growth, zero at the origin 61 64 148 158 165
G(R) 77 170
G(t) 207
g(z,t) 210
Gauss’ formula 105
Goodman’s conjecture xi 163
Green’s formula 106 169
Green’s function 122
H(R) 37
h(z, t’,t") 208
I(E) 84
I(z) 239
Inner radius 124
Inverse function 222
k-symmetric 95 185
Koebe function 2
l(R) 29 199
Landau’s theorem 143
Lebesgue integral 31
Legendre polynomials 231
Legendre polynomials, associated Legendre functions 231
Legendre’s addition theorem 232
Length-area principle 29
Lipschitzian, Lip 104
Lowner’s differential equation 197
M(r,f) 8 33
Major arc 16 19 154
Maximal growth 45
Mean p-valent xi 38 64 165
Milin’s conjecture 230 236
Minor arc 16 21 153
Modules, theory of xi 229
Modulus of continuity 116
Modulus of doubly connected domain 110
n(r, w) 67
n(w) 29 144
O, 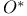 113 113
Odd univalent functions 161 186 248
Omitted values 3 94 150
Order (of f(z) at  ) 42 ) 42
P(R) 29 67 144
p(r, R) 67
p-valent xi 1 28 163
Power series 243
Power series with gaps 98 99 101
Principal frequency 103
Radius of convexity 226
Radius of greatest growth (r. g. g.) 17 48
Radius of starshapedness 227
Real coefficients 13 162 220
Regularity theorems xi 16 49 150
Riemann’s mapping theorem 44 204
Robertson’s conjecture 249
Rogosinski’s conjecture 250
Rouche’s Theorem 147
S 22 36
S(R) 22
Schwarz’s inequality 30
Schwarz’s lemma 11
Schwarz’s reflection principle 44
Slit 204
Slit, sectionally analytic slit 198
Starlike domain 14
Starlike univalent function 14 188
Steiner symmetrization 112
Stolz angle 22
Subordination 250
Symmetrization 112
Symmetrization of condensers 119
Symmetrization of functions 116
Symmetrization, circular or Polya’s 113
Symmetrization, principle of 127
Szego’s conjecture 95
Torsional rigidity 103
Transfinite diameter 103
Transformation 200
Transformation, infinitesimal transformation 203
Typically real 13
Univalent xi 1
Variational method xi 229
Vitali’s convergence theorem 21
W(R) 37 76
[B] for Burkill [1951] 31
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



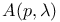 ,
, 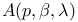
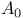
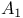 ,
, 
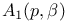
 ,
, 
 ,
, 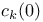 ,
, 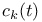
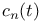
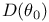
 ,
, 
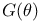
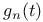
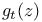
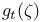
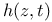
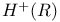
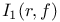
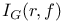
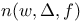
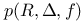
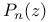 ,
, 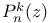
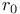 ,
, 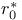
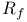
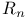
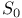
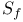
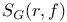
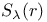
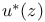


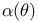
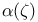
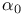

 ,
, 


 , the gamma function
, the gamma function  ,
, 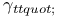
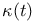
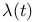
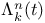
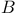
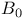
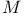
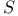



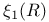 ,
, 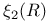
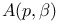
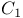 ,
, 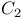 ,...
,... 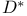
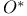
 )
)