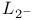|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Porter D., Stirling D.S.G. Ч Integral equations: a practical treatment, from spectral theory to applications |
|
|
 |
| ѕредметный указатель |
 -kernel 72 83 104 105 107 120 122 124 132 160 -kernel 72 83 104 105 107 120 122 124 132 160
AbelТs equation 1 23 291
AbelТs problem 21
Absolute convergence 352
Adjoint equation 61 104 105Ч106
Adjoint operator 102 104Ч105 356Ч357
aerofoil equation 319
AiryТs equation 9 24
Almost everywhere 66 67 114 358Ч359
alternative see УFredholm AlternativeФ
approximation by finite-rank operator 146 245 277 287Ч288
approximation by particular classes of function 274 286
approximation by powers of operator 137 279 280
approximation of compact operator 211 212
approximation of continuous kernel 245 277 288
approximation of eigenvalues, eigenvectors etc. 203Ч240
approximation of solution of inhomogeneous equation 241Ч290
Associated Legendre equation 51Ч52
Banach space 351
Banach space, equations in 63Ч64
Bessel function 20 92 93 181 236 337 338 340
BesselТs equation 45 48 51 92 93 188 235
BesselТs inequality 353
beta function 364
bivariational principle 260
boundary condition, change of 149 162
Boundary condition, mixed 17 18 52 289 335
boundary condition, regular/singular 44
boundary condition, weak 45 52
Boundary-value problem 13 16 34 44 149 150 155 182ff 289 335
Bounded below 164 165
bounded linear map see УOperatorФ
Bounded sequence 351
bounds, complementary 214 215 224 227 232Ч233 261ff 267 285
bounds, pointwise 264 (see also УUpper bounds and lower boundsФ)
Calculus, Fundamental Theorem of 360
Cauchy principal value 304 306 309 365
Cauchy sequence 351
Cauchy singular 7 20
Cauchy singular equation 308ff
change of boundary conditions 149 162
classification of integral equations 2
Closed subset 103 353
Commutativity 133 152 166 352
Compact operator 69 72 75 95Ч138 135 136 211 212
compactness, of operator generated by  -kernel 72 -kernel 72
compactnessof operator generated by weakly singular kernel 76
comparison of operators 176Ч178 227ff
complementary bounds 214 215 224 227 232Ч233 261ff 267 285
completely continuous see УCompact operatorФ
completeness of orthonormal sequence 112 354
completeness, of normed vector space 351
compression of operator 154 182 212
continuity condition on solutions of ODEs 7 8
continuous dependence on data 138 195 243
continuous kernel 126 128Ч131 245
convergence, in the mean 66 120 132 352 355
convergence, in the mean, of sequence of projections 211Ч212
convergence, in the mean, uniform/pointwise see УUniform or pointwise convergenceФ
conversion of differential equation to integral equation 31ff
Convolution 333
Cosine transform 337Ч338 350
coupled equations 16
Degenerate kernel 57ff 70 94 146 150
Dense set 301 356
derivative of eigenvector 189
diagonalisation 113
differential equations, AiryТs equation 9 24
differential equations, associated Legendre equation 51Ч52
differential equations, BesselТs equation 45 48 51 92 93 188 235
differential equations, GegenbauerТs equation 52 230
differential equations, HillТs equation 49
differential equations, LaplaceТs equation 16 18 30 197 335
differential equations, LegendreТs equation 46Ч47
differential equations, TricomiТs equation 17 20
Digamma function 365
Dimension of nullspace 99 106
DiniТs theorem 126 136
Dominant eigenvalue 203
Dominated Convergence Theorem 360
dual bounds see УComplementary boundsФ
dual extremum principles 250 257
dual integral equation 19
Eigenvalue 14 95 99 100 101 108 109 110 120 122 164 206ff 214ff
eigenvalue, approximation of 206ff
eigenvalue, conventions for numbering 141
eigenvalue, inequalities for 146ff 162
eigenvalue, minimax results 142 144 145
Eigenvector 95 101 108 110 120 122 189 206 218ff
eigenvector, approximation of 217ff
eigenvector, completeness of sequence of 112 191 193
eigenvector, conventions for numbering 141
eigenvector, derivative of 189
Elliptic partial differential equation 16 289
equivalence class in 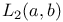 , choice of representative 67 69 114Ч115 , choice of representative 67 69 114Ч115
equivalence of differential equations and integral equations 31ff 41
Essential supremum 93
Essentially bounded 93 155
estimates for eigenvalues 142ff 163ff
existence of solution of integral equation 116 117 342
expansion of kernel 120 122 126 129
expansion of operator, spectral 109Ч110 118
extension of operator 301
extremum principle see УMaximum or minimum principleФ
extremum principles, dual 250 257
Finite rank 69 70 94 102 153 353
Finite-dimensional space 353
first kind equation 3 4 116 117 119 259 291ff 295ff 319ff
Fourier cosine transform 337Ч338 350
Fourier series 354 355 362ff
Fourier sine transform 17 335 350
Fourier transform 1 181 301 302 306 307 330ff
Fredholm alternative 61 69 70 78 104 105 114
Fredholm equation 3
free term 2
FubiniТs Theorem 74 105 361
Functional 205
Fundamental theorem of calculus 360
GalerkinТs method 210 269ff
GalerkinТs method, iterated 277Ч229
Gamma function 364
Gegenbauer polynomial 230
GegenbauerТs equation 52 230
Gram Ч Schmidt process 355
Hermitian kernel 107 120 124 128Ч131 158Ч161
Hermitian matrix 208
Hermitian operator see УSelf-adjointФ
Hilbert space 352
Hilbert transform 307ff
HillТs equation 49
Homogeneous equation 5
image (or range) of operator 103 356 357
inclusion principle 216
inequalities for eigenvalues 146ff 162
infimum, attainment of 144
inhomogeneous equation 5
initial values/initial-value problem 7 33 84
Inner product 352
integral see УLebesgueФ
integral, principal value 304 306 308 309 365
Integro-differential equation 348
Inverse 69 165
invertible/invertibility 69 87 96 97 133 135 160
iterated Galerkin method 277Ч279
iterated kernel 82
iterated trial function 222 253
KantorovichТs method 276 281
KelloggТs method 217
Kernel 2
kernel in sense of of vectors annihilated see УNullspaceФ
| kernel, 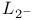 72 83 104 105 107 120 122 124 132 160 72 83 104 105 107 120 122 124 132 160
Kernel, approximation of 245 277 288
kernel, continuous 126 128Ч131 245
Kernel, degenerate 57ff 70 94 146 150
kernel, differentiable 158 161 277 288
kernel, hermitian 107 120 124 128Ч131 158Ч161
kernel, non-negative-valued 159
kernel, Poisson 134
kernel, resolvent 13 115 130Ч132 194
kernel, restriction of domain 172
kernel, Schmidt 123Ч125 132 195
kernel, Schur 74 105 107 133 135 136 160 173
kernel, skew-symmetric 240
kernel, symmetric 14 108
kernel, weakly singular 6 74 76 173 174 291ff
kind (of equation) 3 (see also УFirst kind second
Lagrange multiplier 205 206
Laplace transform operator 178
LaplaceТs equation 16 18 30 197 335
latent root see УEigenvalueФ
Lebesgue Convergence Theorems 360
Lebesgue integral 358
Lebesgue measure/measurable 358 359
LegendreТs equation 46
Linear integral equation 5
Linear map 63
Linear transformation 55
logarithmically singular kernel 6 320
Lower bound 214 215 218Ч219 220Ч221 224Ч225 227 232Ч233 234 255 259 261 263 267 285
Maximum principle 206 248 249 250 256Ч257
maximum, attainment of 144
Mean convergence 66 120 132 352 355
Measurable function 358
Measure 358
MercerТs theorem 126 130 171
minimax results 142 144 145
Minimum principle 206 250 256Ч257 259
minimum, attainment of 144
mixed boundary condition 17 52 289 335
mixed boundary-value problem 17 18 52 289 335
Monotone Convergence Theorem 360
Neumann series 78ff
Non-negative operator 126 129 150 160 163ff
non-self-adjoint equation, bounds for 266Ч267
Non-singular see УInvertibleФ
Norm 64 69 351 352
norm-preserving operator 168 200
Normal operator 199
NullSpace 103 106 356 357
Operator 69 72ff 352
operator, simplifying 294 309 323 339 345 348
operator, simplifying, Volterra 83 291ff
order of integration, reversal of 105 345 361
ordinary differential equation, boundary-value problem 13 34 182ff
ordinary differential equation, conventions about solution 8
ordinary differential equation, conversion to integral equation 7ff 31ff
ordinary differential equation, equivalence to integral equation 41
ordinary differential equation, initial-value problem 7 33 84
Orthogonal complement 356
Orthogonal projection 356 (see also УProjectionФ)
Orthogonal vectors 108 112 353
orthogonality with respect to weight function 192
Orthonormal sequence 99 110 111 112 353 354 355
orthonormal sequence, complete 112 354 355
ParsevalТs theorem 73 354
Partial differential equation 16 30 112 289 335
piecewise constant function 275
Piecewise linear function 275
Poincare Ч Bertrand formula 345
pointwise bounds 264
Pointwise convergence 124
Poisson kernel 134
Positive operator 163Ч202 248 254 259
positive operator, comparison results 176ff
Positive semi-definite see УNon-negativeФ
Power method 220
Principal value 304 306 309 365
principal value integral, reversal of integration order 345
Principles see УMaximum principle minimum
Projection 153 154 160 211 212 356
Projection methods 270
Psi function 365
radius (of spectrum) 86
range (or image) of operator 103 356 357
Rank 69
Rayleigh quotient 139 203 206
Rayleigh Ч Ritz method 207 210 213 214 260 267 272
reciprocal principle 260 268
recovery of properties of solution 67 69 114Ч115
regular boundary value problem 44
residual error 251 271
resolvent kernel/operator 13 115 130Ч132 194
restriction of kernel to smaller domain 172
reversal of order of integration 74 105 345 361
Riesz Ч Fischer theorem 116 120 355
Scalar product see УInner productФ
Schmidt kernel 123Ч125 132 195
SchmidtТs Theorem 124
Schur kernel 74 105 107 133 135 136 160 173
Schwarz quotient 221
SchwarzТs inequality 359
SchwarzТs method 220
second kind equation, definition of 3 5
second-order accuracy 207 246 261
Self-adjoint operator 107ff
Separation of variables 112
simple eigenvalues 225
simplifying operator 294 309 323 339 345 348
Sine transform 17 335 350
singular boundary point 45
singular boundary value problem 44ff
Singular integral see УPrincipal value integralФ
Singular integral equation 3 6 7 20 308ff 330ff
Singular value 118 122
Skew-adjoint 135 240
Spectral radius 86
Spectral theorem 109
Spectrum 96 97 108 109 133 135 280 332
Spectrum of compact operator 98 101 280
Square root 166 196
square-integrable 359
Stationary point 205Ч207 260
stationary principle 206 260 266
Stationary value 204Ч207 261 266
strongly singular (Cauchy singular) 7 20 308ff
Sturm Ч Liouville problem 34 150 155 161 182ff
successive substitution 11
supremum, attainment of 144
Symmetric kernel 14 108
Test function 207
third kind equation 3 4 5
TonelliТs Theorem 361
Trace 120 129 223 225
Trial function 207
TricomiТs equation 17 20
Uniform convergence 124 125 126 127 195
Uniqueness of solutions see УFredholm AlternativeФ
Unitary operator 177 200 303
Upper bound 214 215 219 222Ч223 224Ч225 227 232Ч233 256 261 263 267 285
variation-iteration 222
variational methods, accuracy of 207
Variational Principle 203ff 246ff
Volterra equation 3 9 83
Volterra operator 83 291ff
weak boundary condition 45 52
weakly convergent sequence 99Ч100
weakly singular equation/kernel 6 74 76 173 174 291ff
Weight function 192
Well-posedness 138 195 243
wronskian 32
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



 -kernel
-kernel 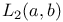 , choice of representative
, choice of representative