Hierarchical clustering methods, evaluation of 211Ч217
Hierarchical clustering methods, example of 221Ч228
Hierarchical clustering methods, single-linkage or nearest-neighbor method 191
Hierarchical clustering methods, Ward's method 193
Holdout method, discriminant function validation 273
Image analysis 109
Implied covariance matrix 444Ч449
Implied covariance matrix, matrix algebra 445Ч446
Implied covariance matrix, models with observable constructs 444Ч446
Implied covariance matrix, models with unobservable constructs 446Ч449
Independence assumption 387Ч388
Independence assumption, lack of tests for 388
Indicator 91
Interdependence methods 4 10Ч12
Interdependence methods, cluster analysis 12
Interdependence methods, correspondence analysis 12
Interdependence methods, factor analysis 11
Interdependence methods, loglinear models 12
Interdependence methods, principal components analysis 11
Interdependence methods, situations for use of 4 10
Interval scale, use of 2Ч3
K-means clustering 205
Kaiser Ч Meyer Ч Olkin measure 116
Kolmogorov Ч Smimov test 378 379
Kurtosis and leptokurtic distribution 375
Kurtosis of univariate normal distribution 375
Kurtosis, normalization of 375
Latent constructs and structural models 13 14
Latent constructs, meaning of 13
Latent factor 91
Leptokurtic distributions, nature of 375
Linear combination, vectors 26Ч27
Linear discriminant function 242
Linear discriminant function, Fisher's 245 277Ч278
LISREL 148Ч177
LISREL, adjusted goodness-of-fit index 159
LISREL, commands 150Ч152
LISREL, constrained analysis 171 173
LISREL, estimated model parameters, evaluation of 162Ч164
LISREL, example of use 174Ч178
LISREL, goodness-of-fit indices 157Ч159
LISREL, initial estimates 152Ч157
LISREL, maximum likelihood estimates 422Ч424
LISREL, McDonald's transformation of the noncentrality parameter (MDN) 159Ч160
LISREL, model fit, evaluation of 157Ч162
LISREL, model information and parameter specifications 152
LISREL, model respecification 164Ч165
LISREL, modification indices 164
LISREL, multigroup analysis 170Ч173
LISREL, null hypothesis test 157
LISREL, null model 160 161
LISREL, one-factor model 153Ч156
LISREL, parameter estimates 162Ч163
LISREL, relative goodness-of-fit index 159
LISREL, relative noncentrality index 160
LISREL, rescaled noncentrality parameter 159 160
LISREL, residual matrix 160Ч162
LISREL, root mean square residual 159
LISREL, squared multiple correlation 163Ч164
LISREL, structural model in 421Ч434
LISREL, terminology related to 148Ч149
LISREL, total coefficient of determination 164
LISREL, Tucker Ч Lewis index 160
LISREL, two-factor model 165Ч170
LISREL, unconstrained analysis 171
Loadings 404
Logistic regression with combination categorical/continuous independent variables 328Ч332
Logistic regression with one categorical variable 321Ч327
Logistic regression with one dependent/more than one independent variable 8
Logistic regression, classification 326Ч327
Logistic regression, compared with discriminant analysis 332Ч333
Logistic regression, computer analysis 321Ч335
Logistic regression, contingency table analysis 327Ч328
Logistic regression, example as illustration of 333Ч335
Logistic regression, example of use 333Ч335
Logistic regression, logistic regression model 319Ч321
Logistic regression, maximum likelihood estimation procedure in 321 324Ч325 339Ч341
Logistic regression, model fit, assessment of 323Ч324
Logistic regression, model information 321
Logistic regression, multiple logistic regression 320
Logistic regression, parameter estimates 324Ч325
Logistic regression, predicted probabilities, association of 325Ч326
Logistic regression, probability and odds in 317Ч321
Logistic regression, situations for use 8 317
Logistic regression, stepwise selection procedure 329 331Ч332
Logit function 320
Logit transformation 383
Loglinear models, situations for use 12
Loss of homogeneity, in cluster analysis 200
Mahalanobis distance 44Ч45
Mahalanobis distance as classification method 258
Mahalanobis distance in cluster analysis 220
Mahalanobis distance in MANOVA 343
Mahalanobis distance, definition of 44
Mahalanobis distance, formula for 44
Mahalanobis distance, squared distance in stepwise discriminant analysis 266
Manova see "Multivariate analysis of variance (MANOVA)"
Maximum likelihood estimation technique in LISREL 422Ч424
Maximum likelihood estimation technique in logistic regression 321 324Ч325 339Ч341
Maximum likelihood estimation technique, computation of 181Ч185
Maximum likelihood estimation technique, computer analysis 148Ч173
McDonald's transformation of the noncentrality parameter (MDN) 159Ч160
Mean, computation of 36
Mean-corrected data, nature of 36
Measure of I 91
Measurement model 14
Measurement scales and number of variables 3Ч4
Measurement scales, interval scale 2Ч3
Measurement scales, nominal scale 2
Measurement scales, ordinal scale 2
Measurement scales, ratio scale 3
Minimum average partial correlation (MAP) 117
Minkowski distance 218
Modification indices, LISREL 164
Monotonic analysis of variance (MONANOVA), situations for use 8Ч9
Multicollinearity and stepwise discriminant analysis 272Ч273
Multicollinearity, population-based 273
Multicollinearity, sample-based 273
Multigroup analysis, with LISREL 170Ч173
Multiple regression as canonical correlation 9
Multiple regression with one dependent/more than one independent variable 5Ч9
Multiple regression, discriminant analysis 262Ч263
Multiple-group discriminant analysis with more than one dependent/one or more independent variables 10
Multiple-group discriminant analysis, analytical approach to 293Ч294
Multiple-group discriminant analysis, classification 293 303Ч304 311Ч312 313
Multiple-group discriminant analysis, computer analysis 294Ч307
Multiple-group discriminant analysis, discrete multiple-group discriminant analysis 10
Multiple-group discriminant analysis, discriminant function 294Ч303
Multiple-group discriminant analysis, F-test in 293 294
Multiple-group discriminant analysis, geometric view of 287Ч293
Multiple-group discriminant analysis, multivariate normal distribution 312Ч316
Multiple-group discriminant analysis, new axes, identification of 289 293
Multiple-group discriminant analysis, number of discriminant functions needed 288Ч289
Multiple-group discriminant analysis, significance of variables, estimation of 294
Multiple-group discriminant analysis, situations for use 10
Multiple-group MANOVA 355Ч366
Multiple-group MANOVA, computer analysis 355Ч366
Multiple-group MANOVA, correlated contrasts 363Ч366
Multiple-group MANOVA, multivariate effects 356
Multiple-group MANOVA, orthogonal contrasts 356Ч363
Multiple-group MANOVA, univariate effects 356
Multivariate analysis of variance (Manova) see also "Multiple-group MANOVA" "Two-group
Multivariate analysis of variance (MANOVA) and multivariate effect size 349Ч350
Multivariate analysis of variance (MANOVA) and univariate effect size 349
Multivariate analysis of variance (MANOVA) with more than one dependent/one or more independent variables 10
Multivariate analysis of variance (MANOVA) with one independent/one dependent variable 343
Multivariate analysis of variance (MANOVA) with one independent/p dependent variables 344Ч346
Multivariate analysis of variance (MANOVA) with one independent/two or more dependent variables 343Ч344
Multivariate analysis of variance (MANOVA) with two independent variables 366Ч370
Multivariate analysis of variance (MANOVA), analytic computations for 346Ч350
| Multivariate analysis of variance (MANOVA), compared to discriminant analysis 350
Multivariate analysis of variance (MANOVA), computer analysis 350Ч370
Multivariate analysis of variance (MANOVA), effect size 348Ч350
Multivariate analysis of variance (MANOVA), geometric view of 342Ч346
Multivariate analysis of variance (MANOVA), multiple-group 355Ч366
Multivariate analysis of variance (MANOVA), multivariate significance tests in 346Ч348
Multivariate analysis of variance (MANOVA), power of test in 349Ч350
Multivariate analysis of variance (MANOVA), situations for use 10 342
Multivariate analysis of variance (MANOVA), two-group 350Ч355
Multivariate analysis of variance (MANOVA), univariate significance tests in 348Ч349
Multivariate analysis, number of variables 5
Multivariate analysis, objectives of 238
Multivariate effect size 349Ч350
Multivariate normal distributions, classification rules for 281Ч283
Multivariate normal distributions, multiple-group discriminant analysis 312Ч316
Multivariate normal distributions, skewness of 375
Multivariate normal distributions, two-group discriminant analysis 281Ч283
Multivariate normality assumption 8
Multivariate normality assumption and discriminant analysis 263Ч264
Multivariate normality tests 380Ч383
Multivariate normality tests, graphical test 380Ч383
Multivariate normality tests, transformations 383
Multivariate significance tests 252
Multivariate significance tests for contrasts 359Ч360 363
Multivariate significance tests in multivariate analysis of variance (MANOVA) 346Ч348
Multivariate significance tests in two-group MANOVA 351 353
Naive prediction rule 260
Nearest-neighbor method, hierarchical clustering method 191
Newton Ч Raphson method 340
No-event 325
Nominal scale, use of 2 7
Nonhierarchical clustering 202Ч211
Nonhierarchical clustering, algorithms in 203Ч207
Nonhierarchical clustering, cluster solution, evaluation/interpretation of 210
Nonhierarchical clustering, computer analysis 207Ч211
Nonhierarchical clustering, evaluation of 217
Nonhierarchical clustering, example of 228Ч232
Nonhierarchical clustering, K-means clustering 205
Nonhierarchical clustering, method to obtain initial seeds 202Ч203
Nonhierarchical clustering, reassignment rales 203
Nonhierarchical clustering, steps in 202
Norm of vector 20
Normality assumptions 375
Nuil hypothesis and power of test 349Ч350 375
Nuil hypothesis and power of test and Type I and Type II errors 374Ч375
Nuil hypothesis and power of test,  statistic for testing of 157 162 statistic for testing of 157 162
Null model 160
Null vector 21
Oblique basis, vectors 31
Oblique factor rotation 140Ч141
Observation space, graphical representation of data in 47Ч50
Odds, in logistic regression 318Ч321
One-factor model with covariance matrix 145Ч147
One-factor model with LISREL 153Ч156
One-factor model, computation of 132Ч133
One-factor model, situations for use 93
Ordinal scale, use of 2
Origin, in Cartesian coordinate system 17Ч19
Orthogonal contrasts, computer analysis 360Ч363
Orthogonal contrasts, multiple-group MANOVA 356Ч363
Orthogonal contrasts, multivariate significance tests for 359Ч360
Orthogonal contrasts, situations for use 357
Orthogonal contrasts, univariate significance tests for 357Ч359
Orthogonal factor model 94
Orthogonal factor rotation 137Ч140
Orthonormal vectors 25 31 32
Parallel analysis 77 79
Parallelogram law of vector addition 22
Pattern loadings 91 94
Pearson product moment correlation 39
Pearson product moment correlation as similarity measure 220
Percent points of normal probability plot correlation coefficient, table of 466
Perceptual map, purpose of 307
Population-based multicollinearity 273
Power of test in MANOVA 350
Power of test, purpose of 349Ч350 375
Principal axis factoring 107
Principal axis factoring for factor extraction 141
Principal components 63 66
Principal components analysis and objective of study 75Ч76
Principal components analysis as dimensional reducing technique 64Ч65
Principal components analysis, algebraic approach to 67Ч71
Principal components analysis, compared to factor analysis 125Ч128
Principal components analysis, compared to two-group discriminant analysis 241Ч242
Principal components analysis, computer analysis 67Ч71
Principal components analysis, eigenstructure of covariance matrix 84Ч85
Principal components analysis, geometric view of 59Ч66
Principal components analysis, goals of 58 66
Principal components analysis, interpretation of principal components 79Ч80
Principal components analysis, issues related to use of 71Ч81
Principal components analysis, number of components to extract 76Ч79
Principal components analysis, singular value decomposition 85Ч86
Principal components analysis, situations for use 11 58
Principal components analysis, spectral decomposition of matrix 86Ч87
Principal components analysis, type of data, effect on analysis 72Ч75
Principal components factoring 103Ч107
Principal components factoring for factor extraction 141Ч142
Principal components scores 63 66
Principal components scores, use of 80
Probabilities, in logistic regression 317Ч321
Projection vector 23 27Ч28
Pythagorean theorem, Euclidian distance computation 19
Q-factor analysis, situations for use 187
Q-Q plot 376Ч378
Quartimax factor rotation 120Ч121 137
R-squared, cluster analysis 198 200
Ratio scale, use of 3
Ray's V, in stepwise discriminant analysis 266
Rectangular Cartesian axes 17
Reflection, of vectors 21
Regression, logistic regression 8
Regression, multiple regression 5Ч9
Regression, simple regression 5
Relative goodness-of-fit index, LISREL 159
Relative noncentrality index 160
Reliability, cluster analysis 221
Rescaled noncentralitv parameter 159 160
Residual matrix, LISREL 160Ч162
Root-mean-square residual 106Ч107 118
Root-mean-square residual, LISREL 159
Root-mean-square total-sample standard deviation of the cluster 198 230
Root-mean-square total-sample standard deviation, formula for 197
Sample-based multicollinearity 273
SAS see "Statistical Analysis System (SAS)"
Saturated models 421
Scalar product, of two vectors 20Ч21 27Ч28
Scale invariant, meaning of 46
Schwartz's criterion 324
Scree plot 76Ч77
Scree plot test 79
Semipartial R-squared, cluster analysis 198 200
Shapiro Ч Wilk test 378 379
Significance tests for main effects 370
Significance tests, MANOVA for two independent variables 367Ч370
Significance tests, multivariate significance tests 346Ч348 351 353
Significance tests, univariate significance tests 348Ч349 353Ч355
Similarity measures 218Ч220
Similarity measures, association coefficients 220
Similarity measures, correlation coefficient 220
Similarity measures, distance measures 218Ч220
Simple regression 5
Simulation percentiles of 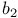 , table of 467 , table of 467
Simulation probability points of 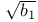 , table of 467 , table of 467
Single-linkage method, hierarchical clustering method 191
Singular value decomposition 85Ч86
Skewness of multivariate normal distribution 375
Skewness of univariate normal distribution 375
Space, observation space 47Ч50
Space, variable space 45Ч46
Spectral decomposition of matrix 86Ч87
|
 |
|
ќ проекте
|
|
ќ проекте



 statistic for testing of
statistic for testing of 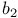 , table of
, table of 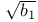 , table of
, table of