|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hinton H. — An introduction to the theory of groups of finite order |
|
|
 |
| Предметный указатель |
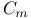 , c, , c,  (point-groups) 113 114 212 (point-groups) 113 114 212
 (point-group) 114 (point-group) 114
Abelian group 51
Absolute invariant 99
Abstract group 55
Adjoined groups 167
Alternating group 79
Appendix 233
Automorphism 136
Automorphisms, group of 137
Bauer’s theorem 145
Bilinear form 16
Birational substitution 12
Burnside’s Theorem 186
Canonical Hermitian form 20
Cayley’s colour-groups 86
Central 63 167
Centre of symmetry 42
Characteristic equation 21
Characteristic equation, of a conjugate set 179
Characteristic equation, series 165
Characteristic equation, subgroup 139
Chief-composition-series 164
Chief-factor-groups 164
Chief-factors 164
Chief-series 164
Circular permutation 7
Class of a group 167
Class of a group, of integral functions 28
Class of a group, of outer automorphisms 137
Cogredient automorphism 136
Cogredient automorphism, groups 167
Collinear transformation 44
Collineation 45
Colour-groups 86
Commutant 133
Commutative elements 1
Commutative elements, group 51
Commutator 4
Commutator, of a group 133
Commutator, subgroup 133
Complete group 137
Completely reducible group 100
Component groups 69
Composite group 63
Composition-factor-groups 158
Composition-factors 158
Composition-series 158
Conformal groups 55
Congruent figures 39
Conjugate complex quantities of a Field 32
Conjugate complex quantities of a Field, elements and subgroups 61
Conjugate complex quantities of a Field, substitution 16
Contragredient automorphism 136
CYCLE 8
Cyclic or cyclical group 60
D, 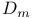 , ,  , , 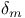 , ,  , , 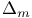 (point-groups) 113 114 115 (point-groups) 113 114 115
Decomposable groups 67
Definite Hermitian form 20
Degree of a cycle 8
Degree of a permutation 6
Degree of a permutation-group 79
Degree of a substitution 12
Degree of a substitution-group 98
Derived groups 166
Determinant of a substitution 16
Dicyclic group 150 170
Dihedral group 113 170
Direct product 69
Distinct representations 179
E, H (point-groups) 113 115
Element 1
Elliptic substitution 27
Enantiomorphous figures 39
Equivalent representations 179
Equivalent representations, system of points, lines,  109 109
Euler’s construction 36
Even permutation 11
Extended point-groups 114
Factor-group 72
Finite group 51
First adjoined group 135
First adjoined group, central 167
First adjoined group, cogredient 135
First adjoined group, derived group 133
Fractional linear substitution 26
Fractional linear substitution-group 98 107
Frobenius’ theorem 75 156
Galois field 29
Gauss’ Theorem 187
General homogeneous linear substitution-group 105
Generator 55
Generators of an Abelian group 126
Geometrical movement 33
Geometrical movement, representation of a movement 40
Gliding-reflexion 38
Gnomonic projection 47
Greatest commonsubgroup(G.C.S.) 66
Group 51
Group of automorphisms 137
Group of cogredient isomorphisms 135
Group of inner automorphisms 135
Group of isomorphisms 137
Group of movements 108
Hamiltonian group 175
Hermitian form 18
Hermitian form, group 104
Hermitian form, invariant 102
Hermitian form, substitution 16
Hints for solution of the examples 189
Holoaxial point-group 111
Holohedral isomorphism 71
Holomorph 139
Homogeneous linear substitution 12 15
Homogeneous linear substitution, linear substitution-group 98
Hyperbolic substitution 27
Hypohermitian form 20
Icosahedral group, E 113
Identical element 1
Identical element, group 57
Imprimitive group 93
Imprimitive group, systems 93
Independent elements 55
Index of a subgroup 58
Infinite group 51
Inner automorphism 136
Integral mark 29
Intransitive group 79
Invariant element 62
Invariant element, of a substitution-group 99
Invariant element, of an Abelian group 127 130
Invariant element, subgroup 63
Inverse conjugate sets 61
Inverse conjugate sets, element 1
Inverse conjugate sets, representations 179
| Inversion about a point 33
Irreducible group 100
Isomorphism 70
Isomorphisms, group of 137
Latin square 82
Lattice 117
Loxodromic substitution 27
Marks of a Galois Field 29
Maximum normal subgroup 158
Merohedral isomorphism 71
Metabelian group 135
Metacyclic group 171
Minimum normal subgroup 162
Modular group 102
Monomial substitution 23
Movement, geometrical 33
Movement, geometrical, of the first or second sort 39
Multiple isomorphism 71
Multiplication 23
Multiplication, table of a group 51
Multiply transitive group 79
n-al rotation or rotatory-inversion 110
Negative permutation 11
Net 115
Non-perspective collineation of order two 47
Normal element 62
Normal element, form of a substitution 26
Normal element, subgroup 63
Normaliser of an element 64
Normaliser of an element, of a subgroup 65
Not-square of a Field 32
O,  (point-groups) 113 115 (point-groups) 113 115
Octahedral group, O 113
Odd permutation 11
Operation 1
Order of a group 51
Order of an element 2
Order of an element relative to a group 51
Orthogonal substitution 16
Outer automorphism 136
Parabolic substitution 27
Partition 58
Perfect group 133
Period of a mark 31
Permutable elements 1
Permutable elements, element and group 61
Permutable elements, groups 67
Permutable elements, movements 33
Permutation 6
Permutation-group 79
Perspective collineation 47
Point-group 108
Pole of a fractional linear substitution 27
Pole of a homogeneous linear substitution 20
Positive Hermitian form 20
Positive Hermitian form, permutation 11
Prime-power Abelian group 130
Prime-power group 142
Primitive group 93
Primitive group, root of congruence 156 169
Primitive group, root of equation in a Field 31
Primitive group, root of Field 32
Product of elements 1
Product of movements 39
Product of permutations 6
Product of substitutions 12 13
Projective transformation 44
Pseudo-substitution 121
Quadratic group 113
Quaternion group 175
Quotient-group 72
Rank of hypohermitian form 20
Real substitution 16
Reciprocal subgroups 183
Reducible group 100
Reflexions, product of two 33
Regular permutation 8
Regular permutation-group 79
Relative invariant 99
Relative invariant, order 51
Representations 179
Residue of a function 28
Resultant of elements 1
Resultant of two reflexions 33
Rodrigue’s construction 36
Rotation-axis 42
Rotatory-inversion 37 41
Rotatory-reflexion 37
Screw 38
Self-conjugate element 62
Self-conjugate element, subgroup 63
Self-inverse conjugate sets 61
Self-inverse conjugate sets, representation 179
Semi-group 51
Series of adjoined groups 167
Series of derived groups 166
Set of characteristics 181
Similar movements 41
Similar movements, permutations 8
Similarity-substitution 23
Simple group 63 107
Simple group, isomorphism 71
Simply transitive group 79
Soluble group 161
Solutions of examples 189
Speciality of a group 167
Square of a Field 32
Stereographic projection 43
Subgroup 57
Substitution 6 12
Substitution-group 98
Sylow subgroup 153
Sylow’s Theorem 152
Symmetric group 79
Symmetric group, substitution 16
Symmetry 42
Symmetry-axis 42
Symmetry-plane 42
T,  , ,  (point-groups) 113 114 (point-groups) 113 114
Tetrahedral group, T 113
Transform of a group 61
Transform of a movement 41
Transform of a permutation 9
Transform of a substitution 14
Transform of an element 3
Transitive permutation-group 79
Transitive permutation-group, sets 91
Translation 33
Translation-group 110
Transposed substitution 16
Transposition 7
Type of an Abelian group 127 130
Type of any group 167
Unitary substitution 16
Vierergruppe 113
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



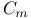 , c,
, c,  (point-groups)
(point-groups)  (point-group)
(point-group) 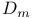 ,
,  ,
, 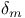 ,
,  ,
, 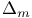 (point-groups)
(point-groups) 
 (point-groups)
(point-groups)  ,
,  (point-groups)
(point-groups)