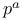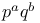|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Blichfeldt H.F. — Finite collineation groups: With an introduction to the theory of groups of operators and substitution groups |
|
|
 |
| Предметный указатель |
Abelian groups 26 43—45
Abstract groups 30 note
Algebraic integer 188
Alternating groups 54 60—61
Associative law 5 30
Bagnera, G. 147 175 176
Bieberbach, L. 97 103 176
Binary groups 63—75
Blichfeldt, H. F. 29 80 102 103 115 116 147 175 176
Boulanger, A. 182
Burnside, W. 4 29 60 80 113 116 123 135 137 138 176
Canonical form 3 24—27
Change of variables 15—17
Characteristic equation 27—28
Characteristics 28 117
Characteristics, general theory 116—138
Characteristics, of inverse and conjugate transformations, and of substitutions 118
Cole, F. N. 29 60
Collineations and collineation groups 10—12
Commutative law 5 31
Components of an intransitive linear group 117
Composition of two groups 125
Congruences 183—84
Conjugate operators, sets, and subgroups 36—38
Conjugate-imaginary groups 18
Cycle of a substitution 52
Cyclotomic number 179
Degree of a substitution group is the number of distinct letters used in the substitutions of the group
Demoivre, A. 187
Determinant of a linear transformation 2 13 exsercise 4
Dickson, L. E. 29 30 61 116 176 177
Differential equations having algebraic solutions 180—82
Dihedral group 70
Diophantine equation 75
Domain 177 180
Equation of the fifth degree 179—80
Equivalent groups 64 129 135
Even substitutions 53
Factor groups 42—43
Finite groups 33
Form problem 179
Frobenius, G. 4 97 102 103 116 119 124 176
Fuchs, L. 21 65 174
Galois, E. 177
Galoisian resolvent 177
Galois’ theory of equations, with Klein’s extension 177—80
Generators 9—10 33 39 exsercise 139
Gordan, P. 65 175
Goursat, E. 165 175
Group characteristics 116—38
Group of an equation 178
Group of similarity-transformations 13 exsercise
Group-matrix 133—35
Groups of linear transformations 7—15
Groups of operators 33 117
Groups of order 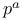 45—50 80 81 45—50 80 81
Groups of order 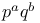 137 137
Groups of substitutions 54 56—59
Groups of the regular polyhedra 69—73
Groups, leaving invariant a quadric surface 169 exsercise 2
Hermite, C. 19
Hermitian form 19
Hermitian invariant 20—21
Hessian group 109
Hilton, H. 29
Holder, O. 60
Huntington, E. V. 30
Icosahedral group 73
Identity, the 3 30 51 9 33
Imprimitive linear groups 76—79
Imprimitive substitution groups 55
Index of a subgroup 34
Intransitive linear groups 17
Intransitive substitution groups 55
Invariant operators and subgroups 39—40
Invariants 120 125
Inverse of a linear transformation 5 7 exsercise 5 6 9 22
Inverse of a substitution 51
Inverse of an operator 31 32 exsercise 33
Irreducible algebraic equations 177
Irreducible differential equations 180
Irreducible groups 22—24
Isomorphism 40—43 117 2°
Jordan, C. 4 60 64 65 73 103 109 115 142 174 175 176 182
| Klein, F. 4 65 142 170 174 175 176 178 180 182
Kronecker, L. 124 186 187
Linear fractional groups 13
Linear groups 8
Linear transformations 1—7
Ling, G. H. 60
Loewy, A. 21
Manning, W. A. 177
Maschke, H. 112 135 141 142 159 163 170 176
Matrices of the transformations of a transitive linear group 135 exsercise 2 176 177
Matrices of the transformations, sum and product of 4 119
Matrix of a linear transformation 2
Miller, G. A. 29 60 113
Mitchell, H. H. 115 175 176
Molien, T. 116 176
Monodromie group 182
Monomial groups 77 80
Moore, E. H. 21 61 141 159 161
Multiplication-table of a group 40
Multipliers of a linear transformation 3 7 exsercise 102 exsercise 2
Netto, E. 29
Non-equivalent groups 64 135
Octahedral group 72
Odd substitutions 53
Operators 1 30
Order of a group of operators 33
Order of a linear group 8 82 127 129 exsercise
Order of a linear transformation 6
Order of a primitive linear group 39 92 103
Order of a subgroup 34
Order of an operator 32 35
Painleve, P. 182
permutations 50
Picard, E. 21
Power of a linear transformation 5
Power of an operator 32
Primitive linear groups 77 94 96 101 103
Primitive substitution groups 55
Product of linear transformations 3—5
Product of matrices 119
Product of operators 30
Product of substitutions 51
Quaternary groups 139—73
Quotient groups 42—43
Reduced set 23
Reducible groups 22—24
Regular substitution group 59 131 135
Roots of unity 186
Schur, I. 4 103 116 119 129 176 177
Schwarz, H. 174
Schwarzian derivative 182
Self-conjugate operators and subgroups 39—40
Set of generators 33
Set of non-equivalent component groups 131
Sets of conjugate operators 36
Sets of conjugate subgroups 38
Sets of imprimitivity (of a linear group) 77
Sets of intransitivity (of a linear group) 18
Sets of intransitivity (of a substitution group) 55
Similarity-transformations 3 7 exsercise 13 exsercise 18 exsercise 40 exsercise
Simple groups 39 58 60—61 137 138 exercise 147
Subgroups 8 34—35 46 49 exsercise
Substitutions 50
Substitutions, written as linear transformations 1 118
Sum of matrices 119
Sylow, L. 46
Sylow’s theorem and Sylow subgroups 46—50 80 147
Symmetric group 54
Systems of imprimitivity (of a substitution group) 55 (see also “Sets”)
Ternary groups 104—15
Tetrahedral group 71
Transform of an operator is the operator into which the given operator is transformed 36
Transformations see “Linear transformations”
Transitive linear groups 17 131
Transitive substitution groups 55
Transposition 53
types of groups 140
Unit circle 94
Unitary form 21—22 24 27
Valentiner group is the group (I) 113
Valentiner, H. 21 65 73 97 115 175 176 180
Variety of a linear transformation and of an abelian group 90
Weber, H. 4
Wiman, A. 180
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте