|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Katok S. — Fuchsian Groups |
|
|
 |
| Предметный указатель |
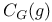 see Centralizer see Centralizer
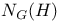 36 see 36 see
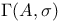 119 119
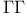 75 see 75 see
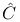 8see Riemann sphere) 8see Riemann sphere)
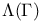 33 see 33 see
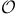 118 see 118 see
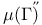 75 see 75 see
 8 see Euclidean 8 see Euclidean
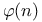 138 see 138 see
Algebraically closed field 115
angle 10
Angle of parallelism 15
C 1see Complex plane
Cauchy — Riemann equations 12 157
Centralizer (of an element g in a group G) 34 see
Commensurable groups 120
Complex plane 1 see
Cosine Rule I 16
Cosine Rule II 16
Cross-ratio 6
Division algebra 113see Skew-field
Euler function 138 see 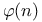
Example 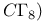 95 148 95 148
Example A 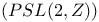 29 34 55 71 74 75 29 34 55 71 74 75
Example B 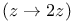 33 49 33 49
Example E 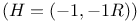 118 124 118 124
Example F 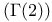 141 141
Example G 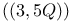 143 143
Example H 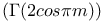 150 150
Fractional linear transformation 2 see PSL(2
Fuchsian group 26
Fuchsian group of the first kind 67
Fuchsian group of the second kind 67
Fuchsian group, arithmetic 112 120
Fuchsian group, cocompact 84
Fuchsian group, congruent points with respect to 70
Fuchsian group, derived from a quaternion algebra 120
Fuchsian group, Dirichlet region for 52
Fuchsian group, Dirichlet region for, boundary of 49 80
Fuchsian group, Dirichlet region for, congruent sides of 73
Fuchsian group, Dirichlet region for, cycle of 70
Fuchsian group, Dirichlet region for, elliptic cycle of 70
Fuchsian group, Dirichlet region for, elliptic vertex of 70
Fuchsian group, Dirichlet region for, Euclidean boundary of 80
Fuchsian group, Dirichlet region for, Euclidean closure of 80
Fuchsian group, Dirichlet region for, extended set of vertices of 70
Fuchsian group, Dirichlet region for, free side of 80
Fuchsian group, Dirichlet region for, side of 70
Fuchsian group, Dirichlet region for, vertex at infinity of 72
Fuchsian group, Dirichlet region for, vertex of 67
Fuchsian group, elementary 37
Fuchsian group, Ford fundamental region for 61
Fuchsian group, fundamental region for 49
Fuchsian group, fundamental region for, locally finite, geometrically finite 80
Fuchsian group, limit set of 33 63 see
Fuchsian group, maximal cyclic parabolic subgroup of 72
Fuchsian group, maximal cyclic parabolic subgroup of, conjugacy classes of 72 see
Fuchsian group, maximal finite cyclic subgroup of 71
Fuchsian group, maximal finite cyclic subgroup of, conjugacy classes of 71
Fuchsian group, parabolic class number of 72 139
Fuchsian group, periods of 71
Fuchsian group, quotient space of 75 see
Fuchsian group, quotient space of, cusp of 75 139
Fuchsian group, quotient space of, marked point of 75
Fuchsian group, signature of 91
Fuchsian group, triangle group 99
F[x] 115 see
Gauss — Bonnet formula 13
Genus (of a surface) 75
Geodesic in H 1
Geodesic- in U 8
H 113 see
H (Hamiltonian quaternion algebra) 113 see
Hecke group 151 see
Horocycle 87
Hyperbolic area in H 11
Hyperbolic area of 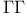 75 see 75 see
Hyperbolic distance in H 2
Hyperbolic distance in H, formulae for 6—7
Hyperbolic distance in U, formulae for 21
Hyperbolic length in H 1
Hyperbolic metric in H 1
Hyperbolic metric in U 7
Hyperbolic plane 1 see
Hyperbolic plane, Euclidean boundary of 8
Hyperbolic plane, Euclidean closure of 8
Hyperbolic plane, model of in H 1
Hyperbolic plane, model of in U 7
| Hyperbolic plane, points at infinity of 8
Hyperbolic polygon 12
Hyperbolic reflection 99
Hyperbolic triangle 12
Hyperbolic trigonometry 15
Hyperbolically convex region 54
id 3 see
Infinity,  6 6
Inverse points 59
Inversion in a circle 58
Isom(H) 4 see
Isom(H), discrete subgroup of 26
Isometric circle 56
Isometry 3
Isometry, anti-conformal 10
Isometry, conformal 10
Isometry, orientation of 10
Isometry, orientation-preserving 10
Isometry, orientation-reversing 10
Isomorphic, 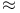 (groups, quaternion algebras, fields) 3 113 114 (groups, quaternion algebras, fields) 3 113 114
Jacobian 12
Jorgensen inequality 41
Locally finite family 27
Metric space, group of homeomorphisms of 27
Metric space, group of homeomorphisms of, acting properly discontinuously on 27
Metric space, group of homeomorphisms of, acting properly discontinuously on, fundamental region for 49
Metric space, group of homeomorphisms of, acting properly discontinuously on, fundamental region for, boundary of a fundamental region F, 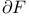 49 49
Metric space, tessellation of 49
Minkowski's Lemma 129
Mobius transformation 2 see
Modular group 29 see Example
Modular group, principal congruence subgroup of level n in 133
Non-Euclidean geometry 1
Normalizer (of a subgroup H in a group G) 36 see
Orbifold 75
Orbit (of a group G, G-orbit) 27
Ordinary point 63
Perpendicular bisector 53
Poincare's theorem 92
Principal circle 8 see Euclidean
PS*L(2,R) 8 see
PSL(2,R) 3 see Mobius
PSL(2,R), conjugate elements in 35
PSL(2,R), elliptic element of 23
PSL(2,R), elliptic element of, fixed point of 23
PSL(2,R), hyperbolic element of 23
PSL(2,R), hyperbolic element of, axis of 24
PSL(2,R), hyperbolic element of, fixed points (repulsive and attractive) of 23
PSL(2,R), identity element in 3 see
PSL(2,R), norm of an element 25—26
PSL(2,R), parabolic element of 23
PSL(2,R), parabolic element of, fixed point of 23
PSL(2,R), trace of an element 3 23
PSL(2,Z) 29 see Example
Pythagorian Theorem 18
Quadratic non-residue 116
Quaternion algebra 113
Quaternion algebra, center of 113
Quaternion algebra, order in 118 see
Quaternion algebra, order in, group of units in 0 of reduced norm 1 119
Quaternion algebra, radical of 113
Quaternion algebra, ramified at a place 117
Quaternion algebra, reduced norm of an element in 115
Quaternion algebra, reduced trace of an element in 115
Quaternion algebra, standard involution in 115
Quaternion algebra, unramified at a place 117
Riemann sphere 6 see
Riemann surface 76
Ring of polynomials over a field F 115 see
S*L(2,R) 8
Siegel's theorem 80
Simple central algebra 113
Sine rule 16
Skew-field 113 see
SL(2,R), identity matrix in, 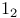 3 3
Sphere of imaginary radius 18
Spherical triangle 19
Totally real algebraic number field 117
Triangle inequality 2
U 7 see
Unimodular group 2 see
Unit disc 1 see
Unit disc, Euclidean boundary of 8 see Principal
Unit disc, Euclidean closure of 8
Upper half-plane 1 see
Upper half-plane, Dirichlet tessellation of 74
Upper half-plane, Dirichlet tessellation of, face of 74
Upper half-plane, Euclidean boundary of 8
Upper half-plane, Euclidean closure of 8
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



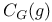
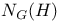
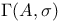
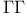
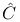
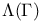
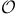
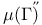

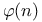

 (groups, quaternion algebras, fields)
(groups, quaternion algebras, fields)