|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Higgins P. — Techniques of Semigroup Theory |
|
|
 |
| Предметный указатель |
 (Green’s relation) 15 (Green’s relation) 15
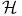 (Green’s relation) 15 (Green’s relation) 15
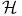 -trivial 21 -trivial 21
 (Green’s relation) 15 (Green’s relation) 15
 (Green’s relation) 15 (Green’s relation) 15
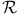 (Green’s relation) 15 (Green’s relation) 15
(u, v)-diagram 74
0-bisimple semigroup 16 22 36
0-direct union 26 42
Absolutely closed semigroup 143
Amalgam 159 165
Amalgam, (weakly, strongly) embeddable 159
Amalgam, core of 159
Amalgam, special 159 160
Amalgamation base (strong, weak) 160 162—163
Amalgamation base (strong, weak), special 160
Amalgamation pair 161 162
Amalgamation property, special 159 161
Amalgamation property, strong 159 161
Amalgamation property, weak 159 161
angle 77
Angle, included edge(s) 77
Angle, included region(s) 77
Angle, interior 77
Angle, sides of 77
Angle, sink- 77 183—184
Angle, source- 77 183—184
Anti-automorphism 11
Anti-homomorphism 11
Anti-isomorphism 11
Anti-representation 11
ARC 69
Arrow (left, right) 60
Automorphism 2
Automorphism of word trees 83
Automorphism, group acting on the left 98
Automorphism, partial 5
Baer — Levi semigroup 14 37 157
Band(s) 2 157
Band(s), (left, right) normal 43
Band(s), 0-rectangular 42
Band(s), commutative 2
Band(s), medial 43
Band(s), normal 43
Band(s), of groups 43
Band(s), of type-T semigroups 37
Band(s), rectangular 2 64 141
Basic products 113
Bimorphism 61
Binary relation(s) 5
Binary relation(s), semigroup of 5
Biorder 60
Biordered set(s) 60—66 110—141
Biordered set(s) of bands 127—130 141
Biordered set(s) of completely regular semigroups 137
Biordered set(s) of eventually regular semigroups 142
Biordered set(s) of regular semigroups 130—133
Biordered set(s), axioms of 111—112
Biordered set(s), isomorphism between 112
Biordered set(s), M-biordered 62 67
Biordered set(s), morphism 61 112 119
Biordered set(s), rectangular 67
Biordered set(s), regular 62 66 137 141
Biordered set(s), solid 135 137 141
Biordered set(s), subset 113 120
Boundary (left, right) 74 177
Brandt semigroup 42 156 165
Bridge 71 217
Cancellative semigroup (left, right) 3 12 29 79
Central element 39
Centre of a tree 69 83
Chain conditions 23
Closed subset of the free group 95
Commutative 2 43 154
Commutative, regular semigroup 40
Commutative, variety 155—156
Complete sequence 136
Completely (0-) simple semigroup 33—37 66 126 141
Completely regular element 4 73
Completely regular semigroup 4 37—41 72 73 157
Completely semisimple 41 59 91 152—153
Component, cyclic 71
Component, even (odd) 209
Component, number 197—199
Component, simple 76
Component, two-sided 74
Congruence(s) 6
Congruence(s), (left, right) congruence extension property 165—166
Congruence(s), generated by a relation 6
Congruence(s), idempotent-consistent 50 123
Congruence(s), idempotent-determined 108
Congruence(s), idempotent-pure 108
Congruence(s), idempotent-separating 50—53 57 58 61 67 104 108
Congruence(s), idempotent-surjective 50
Congruence(s), identity 7
Congruence(s), intersection of 6
Congruence(s), least band 58
Congruence(s), least group 45 53—54 58 98 99
Congruence(s), least inverse 11 59
Congruence(s), least semilattice 37 55
Congruence(s), left (right) 6
Congruence(s), minimum contained in an equivalence 7
Congruence(s), Rees 7
Congruence(s), trace of 54
Congruence(s), universal 6
Consistent pairing of trees 209—210
Convex subset 95
Core of a semigroup 55 59 124
CYCLE 68
Cyclic conjugate 179
Defect of a mapping 3 230
Derivation diagram 74
Diagram 74
Diagram, group 183
Diagram, group, (source- sink-) reduced 185
Diagram, involutary 178
Diagram, over a semigroup 178
Diagram, R- 181—182
Diagram, semigroup 183
Diagram, short 170—171
Diagram, source-reduced (sink-reduced) 78
Diagram, T-minimal 169—170
Digraph 69
Digraph, complete 69
Digraph, functional 70
Digraph, strong 69
Digraph, weak 70
Digraph, weakly connected 70
Dipath 69
Direct product 2
Directed map 177
Dominate 143
Dominion 143 160 165
Dual 2
Dual directional 80
Dual reflection 80
Dual semigroup 11 80
Edge(s) 68
Edge(s), coinitial (coterminal) 77
Edge(s), negative 69
Edge(s), oriented 69
Edge(s), positive 69
Egg-box diagram 16
Elementary R-transition 7
Endomorphism 2 153
Epimorphically embedded 143
Epimorphism 2 13 143
Equational class 10
Equivalence(s) 5 7
Equivalence(s), classes 5
| Equivalence(s), generated by a relation 6
Equivalence(s), intersection of 6
Euler — Mascheroni constant 198
Even-odd offspring 206
Eventual regularity 49—52 67
Factor set 5
Free group 92 178
Free inverse semigroup 10—12 81—97 108
Free monogenic inverse semigroup 81 92
Free product of semigroups 161
Free product with amalgamation 160—161
Free semigroup 9—10 15
Full subset 59
Full transformation semigroup 3 12 29 30 148—149 154 157 166 187—200 204—236
Generalized inverse semigroup 48 57 149—151
Generator(s) 3 10
Generator(s) and relations 9—11
Gluskin’s Lemma 212
Graph 68
Graph, acyclic 68
Graph, centre of 69
Graph, left (right) graph 77—79
Graph, radius of 69
Gravity of a mapping 223 230
Green’s Lemma 17 51 135
Green’s relations 15—16
Green’s relations in a regular  -class 19 -class 19
Group 3 12
Group, embeddable 14 186
Group, inverse 33
Group, left (right) 13 14
Group, maximal 18
Group, of automorphisms 5
Group, of units 5 31
Group, Schiitzenberger 20—21
Group, symmetric 4
Group-bound semigroup 4 12 21 23—28 36 48
Hasse diagram 24
Homomorphism 2
Homomorphism with involution 15
Ideal (left, right) 3
Ideal (left, right), (0-) minimal 29 37
Ideal (left, right), (left, right) principal 3 67 204
Ideal (left, right), 0-minimal left (right) 35—36
Ideal (left, right), extension 7 141
Ideal (left, right), generated by a set 3
Ideal (left, right), order 98
Idempotent 1
Idempotent, central 39
Idempotent, primitive 33 38 42
Idempotent-separating congruence 50—53 57 58 61
Idempotent-separating congruence, maximum 51—53 57 67
Identity element 1
Identity element, right (left) 2
In-tree (out-tree) 70
In-tree (out-tree), root-directed 71
INDEX 4 73
Inflation of a semigroup 15
INTERFACE 169 183
Inverse (of an element) 4
Inverse (of an element) of a relation 7
Inverse (of an element), Moore — Penrose 4
Inverse (of an element), strong 212
Inverse semigroup 4 151 156—157 165
Inverse semigroup, 0-simple 42
Inverse semigroup, E-unitary 98—107
Inverse semigroup, free 11—12 15 81—97 108
Inverse semigroup, free, monogenic 81 92
Inverse semigroup, strict 107
Inverse semigroup, symmetric 4 30 45 105 154 157
Inverse subsemigroup(s) 104 212 222
Inverse subsemigroup(s), entire 106
Involution 11
Isbell’s Zigzag Theorem 144—158
Isbell’s Zigzag Theorem for commutative semigroups 165
Isomorphism 2
Isomorphism of biordered sets 61 112
Isomorphism of Rees semigroups 37
Isomorphism of word trees 83
Iterative range 192—197
Kernel of a homomorphism 5
Kernel of a mapping 5
Kernel of a semigroup 28
Kernel of an orbit of a mapping 72
Label(s) of a walk 83
Label(s), (left, right) boundary 74
Label(s), group 178
Label(s), semigroup 178
Labelling function 178
Labelling function, involutary 178
Lallement’s Lemma 9 15 50
Lattice of (left, right) congruences 7
Lattice of equivalences 7
Lattice of subalgebras 5
Left (right) cycle 78 183—184
Local submonoid(s) 65
Local submonoid(s), subsemigroup(s) 43
Main permutation 72 73
McAlister triple 97
McAlister’s P-Theorem 103
McAlister’s Second Theorem 106 108
Minimal conditions 23—28
Minimal idempotent generating set 231—236
Monogenic semigroup 3 12
Monoid 1
Monoid, bicyclic 31 36 37 58
Monoid, bisimple 22
Monoid, embedding 22
Monoid, free 10
Monomorphism 2 13
Monomorphism of word trees 83
Natural mapping 5
Nilpotent(s) 36 236
Null semigroup 2 29
Orbit(s) of a mapping 72
Orbit(s) of a mapping, acyclic 223
Orbit(s) of a mapping, cyclic 223 236
Orbit(s) of a mapping, of general type 223
Orbit(s) of a mapping, singleton 223
Orthodox semigroup 9 32 42 58 59
P-semigroup(s) 98—109
P-semigroup(s), equivalent 108—109
Partial order(s) 44—49 79
Partial order(s) on Green’s factor sets 16
Partial order(s), compatibility with multiplication 49 65—66
Partial order(s), left (right) partial order on a semigroup 45—46
Partial order(s), natural, partial order on a regular semigroup 46
Partial order(s), natural, partial order on a semigroup 46—49 57
Partial order(s), natural, partial order on an inverse semigroup 44—45 48
Partial order(s), natural, partial order on idempotents 2 57
Partial transformation(s) 4
Partial transformation(s), semigroup of 4 157 166 212 223
Path 68
Path, 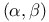 82 82
Path, 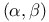 , length of 82 , length of 82
Penrose generalized inverse 4
Period 4 73
Periodic semigroup 4 12 ?6
Permutation identity 156 157—158
Piece 168
Pre-inverse 136 139
Pre-order 16 60 218
Presentation 10
Presentation, cycle-free 77 78
Presentation, Finite 10
Presentation, of a monoid 10
Presentation, of a semigroup 10
Presentation, of the free inverse semigroup 10
Presentation, positive 182
Presentation, reduced 176
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 (Green’s relation)
(Green’s relation) 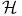 (Green’s relation)
(Green’s relation)  (Green’s relation)
(Green’s relation)  (Green’s relation)
(Green’s relation) 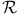 (Green’s relation)
(Green’s relation)