Авторизация
Поиск по указателям
Levine M. — Mixed motives
Обсудите книгу на научном форуме Нашли опечатку?
Название: Mixed motivesАвтор: Levine M. Аннотация: The author constructs and describes a triangulated category of mixed motives over an arbitrary base scheme. The resulting cohomology theory satisfies the Bloch-Ogus axioms; if the base scheme is a smooth scheme of dimension at most one over a field, this cohomology theory agrees with Bloch's higher Chow groups. Most of the classical constructions of cohomology can be made in the motivic setting, including Chern classes from higher X-theory, push-forward for proper maps, Riemann-Roch, duality, as well as an associated motivic homology, Borel-Moore homology and cohomology with compact supports. The motivic category admits a realization functor for each Bloch-Ogus cohomology theory which satisfies certain axioms; as examples the author constructs Betti, etale, and Hodge realizations over smooth base schemes.
Язык: Рубрика: Математика /Алгебра /Алгебраическая геометрия /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1998Количество страниц: 515Добавлена в каталог: 23.03.2005Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
435 436 435 282 377 377 378 2-category 379 2-resolution 239 2-resolution, strict 240 2-resolution, weak 247 Absolute Hodge complexes 273—275 Absolute Hodge complexes, enlarged diagrams 274—275 Adams degree 258 Additive category 381 Additive category, free 384 Adjoining a base-point 361 Adjoining morphisms to a category 384 Adjoining morphisms to a DG tensor category 422—424 Adjoining morphisms to a tensor category 393 Alexander — Whitney map 463 478 Bi-products 380 Bloch’s formula 93 Blow-up distinguished triangle 237—239 Canonical cochains 258 Canonical filtration 277 Canonical topology 482 Canonical truncation 461 Categorical cochain operations 464—466 Category of pairs 385 Cech resolution 53 56 Chern character 169—171 Chern character for diagrams 170 Chern character for higher K-theory 164 Chern character, isomorphism 179 188 Chern classes for 163 Chern classes for higher K-theory 119 122 164 Chern classes for higher K-theory of a diagram 122—126 Chern classes for higher K-theory with support 123 Chern classes for higher K-theory, mod n 124 126 Chern classes for higher K-theory, total 165 Chern classes for line bundles 112 Chern classes for line bundles, properties 112 Chern classes for relative higher K-theory 124 Chern classes for relative higher K-theory with support 124 Chern classes for vector bundles 116 Chern classes, compatibility with localization and relativization 126 Chern classes, naturality 117 Chern classes, properties 116 Chern classes, total 116 164 Chern classes, universal 121 Chow motives 214—215 Chow motives, definition 214 Chow motives, embedding into 215 Chow’s Lemma 237 Classifying scheme 357—358 Classifying scheme, bundles 358 Classifying space 357 Closed simplicial model category 475 Cocontinuous 255 Codegeneracy map 449 Coface map 449 Cohomology over a category 466 467 Compactifiable embedding 225 Compactification 277 Complexes over a DG category 409 411—414 Complexes over a DG category, cone sequence 416 Complexes over a DG category, homotopy category 411 Complexes over a DG category, homotopy category, distinguished triangles 416 Complexes over a DG category, homotopy category, triangulated structure 416—420 Complexes over a DG category, tensor structure 414 Cone for complexes over a DG category 411 Cone for complexes over an additive category 410 Cone for Pre-Tr 411 Cone sequence for complexes over a DG category 416 Cone sequence for complexes over an additive category 410 Connected by a subset 335 Connected in codimension one 335 Connectivity 335 Construction 38—40 Correspondences 210 314 Cosimplicial scheme, motive of a 26 Cosimplicial scheme, very smooth 27 Coskeleton 482 Cup product 453 Cycle class map 47—51 Cycle class map for K-theory 183—185 Cycle class map for units 294 Cycle class map for varieties 48 Cycle class map with support 48 Cycle class map with support for varieties 48 Cycle class map, compatibility with Gysin morphism 138 Cycle class map, motivic 76—78 82 Cycle class map, motivic, injectivity 84 Cycle class map, motivic, isomorphism 88 Cycle class map, motivic, surjectivity 78 82 Cycle class map, naive 71 76 Cycle class map, properties 48—51 Cycle class map, relative 218 Cycle class map, relative, push-forward for 218 Cycle complex, Bloch’s 65 68 Cycle complex, comparison isomorphism 68 Cycle complex, motivic 68 69 Cycle complex, motivic for varieties 77 Cycle map 47—51 Cycle map for varieties 48 Cycle map with support 17 Cycle map with support for varieties 48 Cycles and cycle classes 47 Cycles for 10 Cycles functor 13 38 Cycles of relative dimension d 332 Cycles on simplicial schemes 107 110 Cycles on simplicial schemes, products 109 Cycles, basic definition 10 Cycles, effective 332 Cycles, equi-dimensional, properties of 352—356 Cycles, equi-dimensional, pull-back for 346 Cycles, functoriality 10 Cycles, intersection multiplicity 333 Cycles, intersection multiplicity over a normal base 340 Cycles, intersection multiplicity over a reduced base 349 Cycles, relative 181 331 de Rham functor 282 Decalage 278 Decomposition into type 445 Deformation diagram 131 Differential graded category 381 Differential graded category, homotopy equivalence 420 DIMENSION 331 Dimension over a scheme 331 Discriminant 239 Distinguished octahedra 429 Dold — Kan equivalence 362 Dual of a morphism 193 Dual of an object 192 Dual, canonical 194 Duality criterion for a tensor category 195—197 Duality criterion for a triangulated tensor category 204 Duality in tensor categories 191 Duality in triangulated tensor categories 198 Duality involution for a graded tensor category 195 Duality involution for a tensor category 194 Duality involution for a triangulated tensor category 201 204 Duality involution for smooth projective schemes 205—206 Duality involution for the triangulated motivic category 206 207 Duality involution for the triangulated Tate category 235 Duality involution, explicit formulae 210—214 Effective motives, category of 311 Effective motives, tensor product for 312 Eilenberg — maclane map 477 Equi-dimensional, cycle 332 Equi-dimensional, scheme 331 Etale site 482 Exact category 358 Excision isomorphism 18 Extended total complex 455 External product 391 External product, categorical 391 External product, universal 392 Fiber functor 483 Fiber functor, associated pro-object 485 Fiber functor, stalk 484 Fibrant, functor 475 Fibrant, simplicial set 475 Finite category 468 Flat, inverse system 271 Flat, presheaf 256 Flat, sheaf 256 Flatness 497 General linear group 358 Generated by a set of objects 425 Generic projection 95 Geometric cohomology theory 255 257 Geometric motives, category of 313 Geometric point 269 331 Gluing cycles 347 Godement resolution 486 490—499 Godement resolution and cohomology with support 490 492 Godement resolution and flatness 499 Godement resolution and sheaf cohomology 490 Godement resolution, associated complex 490 Godement resolution, products 493 496 Good compactifications 224 Good compactifications, duality for 224 Graded category 381 Graded homomorphism 383 Graded symmetric monoidal category 436 Graded symmetric monoidal category, punctual 436 Grothendieck group 359 Grothendieck pre-topology 481 Grothendieck site 481 Grothendieck site, presheaf on a 482 Grothendieck site, sheaf on a 482 Grothendieck topology 481 Grothendieck topology, covering families 481 Group homology 357 Gysin distinguished triangle 132 Gysin isomorphism 18 Gysin morphism 20 130 141 Gysin morphism for a closed embedding 131—132 Gysin morphism for a split embedding 130—131 Gysin morphism, compatibility with cycle classes 138 Gysin morphism, compatibility with products 142 Gysin morphism, functoriality 132 Gysin morphism, properties 132 Gysin sequence 132 Higher Chow groups and motivic cohomology 103 105 Higher Chow, Bloch’s 65 66 Higher Chow, comparison isomorphism 71\ Higher Chow, motivic 75—77 Higher Chow, motivic and hypercohomology 77 Higher Chow, motivic and X-theory 179 Higher Chow, motivic for varieties 77 Higher Chow, naive 70 Higher Chow, naive for varieties 72 Homotopy category of a DG category 409 Homotopy category of the category of complexes 411 Homotopy commutative product 463 Homotopy commutativity 322 441 445 455 Homotopy equivalence of DG categories 420 Homotopy fiber 127 Homotopy limit for simplicial sets 474—475 Homotopy limit, additive 467 468 471 Homotopy limit, additive and cohomology 473 Homotopy limit, additive and hypercohomology 474 Homotopy limit, additive, distinguished triangle 472 Homotopy limit, additive, functoriality 472 Homotopy limit, additive, non-degenerate 471 Homotopy one point category 13 435 440—441 Homotopy one point category, universal mapping property 441 Homotopy property 17 Homotopy property for homological motives 216 Homotopy property for motives of diagrams 35 Homotopy property for motives of schemes 19 Hurewicz map 362—363 Hurewicz map for diagrams 363—364 Hurewicz map, compatibility with products 364—369 Hypercohomology 62 Hypercohomology for motives 63 64 Hypercover 482 Hypercover of a sheaf 483 Hypercover of an object 483 Hyperresolutions for motives 59 Hyperresolutions for motives, maps of 59 Hyperresolutions for motives, the category of 59 61 Hyperresolutions, cubical 237 240 Hyperresolutions, cubical, category of 240 Hyperresolutions, cubical, strict 240 Hyperresolutions, cubical, weak 247 Index of inseparability 338 Intersection multiplicity on a regular scheme 333 Intersection multiplicity over a normal base 340 Intersection multiplicity over a reduced base 349 Inverse systems of sheaves 269 Inverse systems of Tate sheaves 270 Inverse systems, category of 269—270 Inverse systems, category of internal Horn 270 Inverse systems, category of tensor structure 270 Inverse systems, continuous hypercohomology for 270 Inverse systems, strongly acyclic 271 Inverse systems, strongly normalized 271 K-group with support 123 K-group, relative 123 K-group, relative with support 124 K-theory and homology of GL 362 K-theory for diagrams 360 K-theory for schemes 358 Kunneth isomorphism 18 Kunneth isomorphism for compactly supported motives 217 Kunneth isomorphism for diagrams 36 Kunneth isomorphism for homological motives 216 L-functions of motives 292 Lambda ring 161 Lambda ring, Adams operations 180 Lambda ring, Adams operations for higher K-theory 181 Lambda ring, augmented 180 Lambda ring, gamma filtration 180 Lambda ring, special 162—163 Lambda ring, structure for 163 Lambda ring, structure for higher K-theory 179—180 Leibnitz rule 295 Localization of a triangulated category 425—426 Localization of a triangulated tensor category 426 Localization, connecting homomorphism 299—302 Localization, distinguished triangle 22 Localization, distinguished triangle for homological motives 216 Localization, distinguished triangle for motives with support 22 Localization, distinguished triangle for relative motives 34 Localization, sequence 126 129 Localization, sequence, compatibility with Chern classes 128—130 MAH complex 285 Mayer — Vietoris for homological motives 216 Mayer — Vietoris for motives 21 Mayer — Vietoris for motives with support 22 Milnor K-groups 293 298—303 Milnor K-groups and motivic cohomology 298 Milnor K-groups, tame symbol 302 Milnor K-sheaf 303 Mixed absolute Hodge complex 285
Реклама
 |
|
О проекте
|
|
О проекте



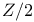 -set
-set  -module, holonomic
-module, holonomic 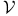 -category
-category