|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Evans A. — Orthomorphism Graphs of Groups (Lecture Notes in Mathematics) |
|
|
 |
| Предметный указатель |
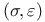 -systems 27 -systems 27
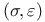 -systems, equivalence of- 27 -systems, equivalence of- 27
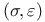 -systems, order of 27 -systems, order of 27
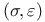 -systems, rank of the solution space of- 27 -systems, rank of the solution space of- 27
Adjacency of mappings 1
Adjacency of orthomorphisms 2
Affine planes 9—13
Almost simple groups 24
Aschbacher's reduction 24
Automorphisms of left neofields 15—16
Automorphisms of Orth(G) 3—5
Automorphisms, fixed point free- 51—54
Cartesian groups 11
Cartesian planes 11
Cayley tables of groups 6
CIP-neofields 18
Clique numbers of orthomorphism graphs 2
CMP-neofields 18
Collineations of nets 11—12
Commutative left neofields 16—17
Complete mapping polynomials 44
Complete mappings 1
Complete sets of mutually orthogonal Latin squares 7
Complete sets of orthomorphisms 3 73—76
Components of partial congruence partitions 50
Congruences of Orth(G) 3—5
Cyclic neofields 17—18
Cyclotomic orthomorphisms 41—43
Cyclotomy classes 40—41
Cyclotomy numbers 41
Degrees of orthomorphisms 2
Degrees of partial congruence partitions 50
Desarguesian affine planes 10
Designs, Knut Vic- 62—63
Designs, resolvable transversal- 9—11
Designs, transversal- 9—11
Difference families, 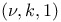 65—66 65—66
Difference families, 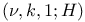 66—67 66—67
Difference matrices 7—8 67—68
Difference sets, 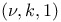 63—64 63—64
Difference sets, 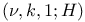 64—65 64—65
Direction of a translation of a net 11
Duals of complete sets of orthomorphisms 13
Equivalence of 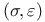 -systems 27 -systems 27
Exchange inverse property of a left neofield 16—17
Exdomain elements of near orthomorphisms 14
Fixed point free automorphisms 51 52 54
Generalized Hadamard matrices 8—9 74
Hermite's criterion 44
Homologies of near orthomorphisms 16
Homologies of Orth(G) 3—5
HP-systems 24
Inverse property of a left neofield 16—17
Inversions of Orth(G) 3—5
Knut Vic designs 62—63
Latin squares 6—7 62
Latin squares, Based on groups 6
Latin squares, complete sets of mutually orthogonal— 7
Latin squares, maximal sets of mutually orthogonal— 7 67—73
Latin squares, orthogonality of- 6
Left inverse property of a left neofield 16—17
Left neofields 14—17
Linear orthomorphisms 35—36 38—41
LXP-neofields 18
Maximal difference matrices 8 67—68
Maximal sets of mutually orthogonal Latin squares 7 67—73
Mutually orthogonal Latin squares based on groups 6
Near orthomorphisms 14—17
Neighbors of orthomorphisms 2
Neofields 14—18
Neofields, CIP- 18
Neofields, CMP- 18
Neofields, Commutative left- 16—17
Neofields, cyclic- 17—18
Neofields, exchange inverse property of left- 16—17
Neofields, inverse property of left- 16—17
Neofields, left inverse property of left- 16—17
| Neofields, left- 14—17
Neofields, LXP- 18
Neofields, order of of left- 14
Neofields, presentation function of of left- 14—15
Neofields, right inverse property of left- 16—17
Neofields, RXP- 18
Neofields, XIP- 18
Neofields, XMP- 18
Nets 9—12
Nets, collineations of- 11—12
Nets, direction of a translation of a- 11
Nets, Splitting translation- 50
Nets, translation- 50 52
Nets, translations of- 11
Normalized permutation polynomials 45—46
Order of 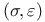 -systems 27 -systems 27
Order of a representation of a graph 59
Order of left neofields 14
Orth(G) 2
Orthogonal Latin square graphs 59
Orthogonal mappings 1
Orthogonality of Latin squares 6
Orthomorphism graphs of groups 2
Orthomorphism graphs of groups, clique numbers of- 2
Orthomorphism graphs of groups, r-cliques of- 2
Orthomorphism polynomials 44—47 49 71 79—82
Partial congruence partitions 50
Partial congruence partitions, components of- 50
Partial congruence partitions, degrees of- 50
Permutation polynomials 44—46 48
Permutation polynomials, normalized- 45—46
Permutations of groups 1
Planes, affine- 9—13
Planes, Cartesian- 11 73
Planes, desarguesian- 10
Planes, projective- 9
Polynomials, complete mapping- 44 49
Polynomials, normalized permutation- 45—46
Polynomials, orthomorphism- 44—47 49 71 79—82
Polynomials, Permutation- 44—46 48
Presentation functions of left neofields 14—15
Projective planes 9
Qrthomorphisms 1
Qrthomorphisms, adjacency of- 2
Qrthomorphisms, complete sets of- 3 73—76
Qrthomorphisms, cyclotomic- 41—43 47—49
Qrthomorphisms, degrees of- 2
Qrthomorphisms, duals of complete sets of- 13
Qrthomorphisms, linear- 35—36 38—41
Qrthomorphisms, near- 14—17
Qrthomorphisms, neighbors of- 2
Qrthomorphisms, quadratic- 36—41 48 71—72 75—76
Quadratic orthomorphisms . . . 36—41 48 71—72 75—76
Quasisimple groups 24
r-cliques of orthomorphism graphs 2
Rank of the solution space of a 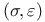 -system 27 -system 27
Reflections of Orth(G) 3—5
Representations of graphs 58—59
Resolvable transversal designs 9—11
Right inverse property of a left neofield 16—17
RXP-neofields 18
Splitting translation nets 50
Starters 1
Strong complete mappings 60—62
The orthomorphism graph of a group, Orth(G) 2
The orthomorphism graph of a group, Orth(G), automorphisms of- 3—5
The orthomorphism graph of a group, Orth(G), congruences of- 3—5
The orthomorphism graph of a group, Orth(G), inversions of- 3—5
The orthomorphism graph of a group, Orth(G), reflections of- 3—5
The orthomorphism graph of a group, Orth(G), translations of- 3—5
Translation nets 50 52
Translations of nets 11
Translations of Orth(G) 3—5
Transversal designs 9—11
Transversal designs, resolvable- 9—11
XIP-neofields 18
XMP-neofields 18
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



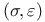 -systems
-systems