Àâòîðèçàöèÿ
Ïîèñê ïî óêàçàòåëÿì
Davis M., Sigal R., Weyuker E. — Computability, complexity, and languages: Fundamentals of theoretical computer science
Îáñóäèòå êíèãó íà íàó÷íîì ôîðóìå Íàøëè îïå÷àòêó?
Íàçâàíèå: Computability, complexity, and languages: Fundamentals of theoretical computer scienceÀâòîðû: Davis M., Sigal R., Weyuker E.Àííîòàöèÿ: This introductory text covers the key areas of computer science, including recursive function theory, formal languages, and automata. It assumes a minimal background in formal mathematics. The book is divided into five parts: Computability, Grammars and Automata, Logic, Complexity, and Unsolvability. * Computability theory is introduced in a manner that makes maximum use of previous programming experience, including a "universal" program that takes up less than a page.* The number of exercises included has more than tripled.* Automata theory, computational logic, and complexity theory are presented in a flexible manner, and can be covered in a variety of different arrangements.
ßçûê: Ðóáðèêà: Computer science /Ñòàòóñ ïðåäìåòíîãî óêàçàòåëÿ: Ãîòîâ óêàçàòåëü ñ íîìåðàìè ñòðàíèö ed2k: ed2k stats Èçäàíèå: 2-nd editionÃîä èçäàíèÿ: 1994Êîëè÷åñòâî ñòðàíèö: 628Äîáàâëåíà â êàòàëîã: 30.03.2014Îïåðàöèè: Ïîëîæèòü íà ïîëêó |
Ñêîïèðîâàòü ññûëêó äëÿ ôîðóìà | Ñêîïèðîâàòü ID
Ïðåäìåòíûé óêàçàòåëü
Induction, structural 500—501 516 517 518 534 535 558 567 571 inf 225 Initial functions 42 76 108 Instantaneous descriptions 27 see instructions 17—18 26 65—67 197 Instructions, conditional branch 18 35 Instructions, decrement 18 Instructions, increment 18 Instructions, labeled 26 Instructions, numbers of 65—67 74 201 Instructions, of 122 Instructions, of Post — Turing programs 129 Instructions, oracle 197—198 201 Instructions, unlabeled 26 Instructions, while 103 Interpretations, continuous 513 539 Interpretations, for predicate logic vocabularies 377 382 411 Interpretations, for typed vocabularies 512—513 539 546 Interpretations, Herbrand ideal 546 interpreters 70 Intractability 444 457 459 Isomorphisms 485 Iteration theorem see "Parameter theorem" Jech, Thomas 594 Johnson, David S. 593 Jumps of sets 213 Kleene's hierarchy theorem 216 Kleene's theorem 253—260 Kuroda, S.Y. 331 339 l'Hospital's rule 442 labels 18 25 Landweber, P.S. 331 Languages 4 see Languages, accepted by deterministic Turing machines 189 Languages, accepted by finite automata 239 Languages, accepted by linear bounded automata 330—337 Languages, accepted by nondeterministic finite automata 243 Languages, accepted by nondeterministic Turing machines 160—161 186 189 Languages, accepted by pushdown automata 311—323 Languages, accepted by Turing machines 153—157 189 Languages, generated by grammars 186 189 270 327—328 Languages, in NP see "NP" Languages, inherently ambiguous 301 Languages, NP-complete see "NP-completeness" Languages, NP-hard 449 Languages, polynomial-time decidable see "P" Languages, recursive 156 190 328 446 Languages, recursively enumerable see "r.e. languages" Languages, spanning sets for 263 Lattices 485 502 Lazy functional languages 553 Least upper bounds 476 Lee, R.C.T. 593 Lemmas 8 Lewis, Harry R. 594 Lexical analysis 323 Linear bounded automata 330—343 Linear bounded automata, deterministic 336 337 343 Linears orders 472 see Linked conjunct procedures 400 Lisp 507 Lists, finite 541 552 Lists, infinite 553 588—590 Lists, prefix 553 Literals 354 447—448 Loeckx, Jacques 594 Logic see "Propositional calculus" "Quantification Logic programming languages 403 Logical consequence 382—388 Loveland, Donald W. 594 m-completeness 92 93 97 210 217 Machtey, Michael 427 594 Macro expansions 20—24 33 35 121—123 macros 20 32—37 122—123 127 Macros for Post — Turing programs 136 137 Many-one reducibility 90—95 207—211 Markov, A.A. 178 Mates 355 357—358 366—367 397—398 399 see Meaning functions, denotational 527 533 536 557 573—574 586 Meaning functions, operational 566 573—574 585—586 Metavariables 506 Minimal unsatisfiability 366—367 392 395 see truth Minimalization 55—59 75 76 77 200 578 Minimalization, bounded 55—58 Minimalization, proper 77 Minimalization, unbounded 57—58 Models 380 382 384 385 406 412 Models, countable 406 Myhill — Nerode theorem 263—264 Myhill, John 232 263 n-tuples 2 Natural numbers 1 NDFA 243 see nondeterministic" Nerode, Anil 263 Normal Form Theorem 75 Normal processes 192—195 Normal productions 193 NP 446—451 456 457—463 NP-complete problems, 2-COLORABILITY 461 NP-complete problems, 2-SAT 461—462 NP-complete problems, 3-DIMENSIONAL-MATCHING 460 NP-complete problems, 3-SAT 457—458 460 461 462 NP-complete problems, CHROMATIC-NUMBER 461 462 NP-complete problems, COMPLETE-SUBGRAPH 458—459 462 NP-complete problems, EXACT-COVER 462 NP-complete problems, HALF-SAT 456 NP-complete problems, HAMILTONIAN-CIRCUIT 460 462 NP-complete problems, INTEGER-PROGRAMMING 460 NP-complete problems, KNAPSACK 463 NP-complete problems, LONGEST-COMMON-SUBSEQUENCE 462 NP-complete problems, MAX-CLIQUE 459 NP-complete problems, MULTIPROCESSOR-SCHEDULING 463 NP-complete problems, PARTITION 460 462 463 NP-complete problems, QUADRATIC-DIOPHANTINE-EQUATIONS 461 NP-complete problems, RECORD-ALLOCATION 463 NP-complete problems, SAT 446—456 458 NP-complete problems, SET-COVER 460 NP-complete problems, STRAIGHTLINE-PROGRAM-IN-EQUIVALENCE 461 NP-complete problems, SUBGRAPH-ISOMORPHISM 462 NP-complete problems, SUBSET-SUM 462 NP-complete problems, TASK-SEQUENCING 463 NP-complete problems, TRAVELING-VENDOR 462 NP-complete problems, VERTEX-COVER 459—460 462 NP-completeness 208 448 449 451 457—463 NP-hardness 449 451 457 NPSPACE 451 NTime 450 Numeral systems 408 One-One Reducibility 207—211 Oracles 197—200 Ordered pairs 2 Orderings see also "Partial orders" Orderings, 474 481 Orderings, Cartesian product 472 479 Orderings, continuous function space 488 Orderings, function space 473 480 Orderings, lexicographic 484 P 444—446 448 449 456 461 Pairing function theorem 60 Pairing functions 59—60 65 66 67 74—75 83 106 107 110 203 228 232 435 Palindromes 241 265 Papadimitriou, Christos H. 594 Parameter Theorem 85—88 92 93 96 99 209 225 226 229 231 428 435 Parameter theorem, relativized 205—206 209 Parsing 324—326 Partial orders 472—475 see Partial orders, bottom elements of 471 477 Partial orders, bounded-complete 485 494 Partial orders, chains in 477 499 Partial orders, ideal completions of 483 Partial orders, ideals of 482—483 546—556 Partial orders, isomorphic 485 486 493 544 Partial orders, principal ideals of 482 Pascal 279 323 326 438 Pigeon-hole principle 260 264 266 451 Polynomial-time computability 445 Polynomial-time decidability 444 Polynomial-time reducibility 208 448—449 457 Polynomials 441 442 Post Correspondence Problem 181—186 299—301 322 Post correspondence system 181 300 Post Words 171—175 177 187 Post — Turing programs 129—144 145 149 150 161 200 Post's lemma 177 Post's theorem 217—224 228 Post, Emil L. 129 178 181 Power sets 472 PRC classes 42—44 49—56 62 63 79 84 199 Predecessor function 46 Predicate logic 375—415 predicates 5—7 10 34—35 68 217—224 419 Predicates, admissible 499 502 537 Predicates, arithmetic 223—224 Predicates, computable 34—35 50 68 85 Predicates, primitive recursive 49—51 78 187 259—260 Predicates, recursive 419 Prenex normal form 384 Prenex sentences 384 Prime numbers 8 54 56—57 69 265 267 588 productions see "Context-free grammars productions "Semi-Thue Productions, null 269 Program verification 536 Programming systems 88 Programming systems, acceptable 88 105 128 144 153 Programs 17—28 65—67 197 see Programs, as a data structure system 542 Programs, computations of 27 Programs, correct 536 Programs, for string computations 121—26 Programs, functions computed by 19 22—24 28—32 198 Programs, G-computations of 198 201 Programs, instantaneous descriptions of 27 Programs, length of 26 Programs, numbers of 65—67 68 70 74—76 86 89 90 95—97 97—105 201 224 225 Programs, snapshots of 27—28 29 70 74—76 197—198 420 Programs, states of 26 197 Programs, straightline 32 Programs, universal 70 Programs, with oracles 197—198 Projection functions 42 478 PROLOG 403 Proof by contradiction 8—9 Proofs 8 Propositional calculus 347—373 Propositional connectives 347 Propositional variables 347 PSPACE 450 451 Pumping lemma 260—262 264 267 see Pure literal rule 362 363 Pushdown automata 308—323 Pushdown automata, atomic 314 315 316 Pushdown automata, computations by 311—323 Pushdown automata, deterministic 311 313 315 Pushdown automata, generalized 321 Pushdown automata, languages accepted by 311—323 Pushdown automata, nondeterministic 312 315 Pushdown automata, transitions of 310 Quadruples 145 330—333 338 454—455 Quantification theory 375—415 Quantifiers 7—8 Quantifiers, alternating 223 Quantifiers, bounded 7 53—55 Quantifiers, in predicate logic 376 Quintuples 149 r.e. languages 154—157 161 188 189 327 344 371 391—392 407—408 r.e. sets 78—85 88 90—95 209—211 231 391 407 408 409 592 r.e. sets, relative to an oracle 211—215 Rates of growth 439—443 Recursion 40 41 44 45 76 77 100 200 348 496 501 576 Recursion equations 40 41 44 45 46 47 62 63 100 104 309 314 505 508 see Recursion theorem 97—105 111 428 431 see Recursion theorem, first 501 503 Recursion theorem, second 501 Recursion theory 31 see Recursion, course-of-values 62 109 Recursion, primitive 40 41 100 106 108 Recursion, simultaneous 62 Recursion, unnested double 63 Recursive function theory see "Computability theory" Recursive isomorphisms 231—234 Recursive operators 503 Recursive permutations 231—234 Recursive relatedness theorem 422 424 425 437 Recursively enumerable languages see "r.e. languages" Recursively enumerable sets see "r.e. sets" Redexes 559 Reducibilities 90—95 96 207—211 see "One-one "Polynomial-time Reducibilities, completeness with respect to 92—93 208 210 Regular expressions 256—260 Regular grammars 280—285 327 Regular languages 237—267 280—285 292 304 306 327—328 450 see Regular languages, and finite automata 237—242 Regular languages, and nondeterministic finite automata 242—247 Regular languages, closure properties for 249—260 Regular languages, examples of 247—249 Regular languages, infinite 261 Regular languages, represented by regular expressions 257 Regular languages, spanning sets for 263—267 Relation symbols 375 Relativization 199 Relativization of computability 198 Relativization of enumeration theorem 213 Relativization of parameter theorem 205—206 Relativization of recursive enumerability 211—215 Relativization of step-counter theorem 202—204 Relativization of universality theorem 201—202 Remainder 56 114 Representable elements see "W-structures representable Resolution in predicate logic 400—404 Resolution in propositional calculus 367—370 393 402 444 Resolution, derivations 367 402 Resolution, refutations 367 402 Resolvents 367 Rewrite rules 169 559 see Rewriting strategies 559 560 564—565 Rice — Shapiro theorem 231 Rice's theorem 95—97 103 230—231 Right quotients 266 297 Robinson's general resolution theorem 402 Rogers, Hartley 594 Rooted sentences 412—414 S-m-n theorem see "Parameter theorem" SAT 446—456 458 Satisfiability, finite 370 Satisfiability, in predicate logic 380 383 384 385 389—391 394 411 Satisfiability, problem 358 Satisfiability, truth-functional 348—352 352—353 355—356 358 364 366—367 372 389—391 405 444 446—456 scaling factors 421 Schmidt, David 594 Scott domains 494 Self-embedding grammars 284 Self-reference 98 99 Self-reproducing program 100 Semantics see also "Meaning functions" Semantics, denotational 468 499 505—556 Semantics, of 26—28 Semantics, of formulas in predicate logic 377—382 Semantics, of programming languages 467—468 Semantics, of propositional formulas 348 Semantics, of regular expressions 257
Ðåêëàìà
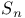programs 
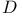-choice function 
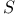programs 
|
|
Î ïðîåêòå