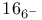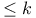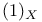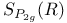Lange H., Birkenhake C. — Complex Abelian Varieties (Grundlehren Der Mathematischen Wissenschaften) :: Электронная библиотека попечительского совета мехмата МГУ

Главная Ex Libris Книги Журналы Статьи Серии Каталог Wanted Загрузка ХудЛит Справка Поиск по индексам Поиск Форум

Авторизация

Поиск по указателям

Lange H., Birkenhake C. — Complex Abelian Varieties (Grundlehren Der Mathematischen Wissenschaften)

Обсудите книгу на научном форуме

Нашли опечатку?
Выделите ее мышкой и нажмите Ctrl+Enter

Название: Complex Abelian Varieties (Grundlehren Der Mathematischen Wissenschaften)

Авторы: Lange H., Birkenhake C.

Аннотация:

The subject of this book is the theory of abelian varieties over the field of complex numbers. It covers the main results of the theory, both classic and recent, in modern language. It is intended to give a comprehensive introduction to the field, but also to serve as a reference. The focal topics are the projective embeddings of an abelian variety, their equations and geometric properties. Moreover several moduli spaces of abelian varieties with additional structure are constructed. Some special results on Jacobians and Prym varieties allow applications to the theory of algebraic curves.

The second edition contains five new chapters which present some of the most important recent result on the subject. Among them are results on automorphisms and vector bundles on abelian varieties, algebraic cycles and the Hodge conjecture.

Язык:

Рубрика: Математика/

Статус предметного указателя: Готов указатель с номерами страниц

ed2k: ed2k stats

Год издания: 1992

Количество страниц: 441

Добавлена в каталог: 10.03.2014

Операции: Положить на полку | Скопировать ссылку для форума | Скопировать ID

Предметный указатель

Abel — Jacobi map      324 325
Abel — Jacobi theorem      325
Abel — Prym map      372
Abelian variety      72
Abelian variety with complex multiplication      268 272
Abelian variety with real multiplication      250
Abelian variety with totally definite quaternion multiplication      262
Abelian variety with totally indefinite quaternion multiplication      259
Action on a family of abelian varieties      237
Addition formula      208
Addition map      7
Adjunction formula      289
Albanese map      361
Albanese torus      361
Albanese variety      339
Algebraic complex analytic space      409
Algebraic cycle      107 129 130
Algebraic dimension      86 318
Algebraic equivalence of line bundles      89
Ample line bundle      85
Analytic equivalence      40
Analytic norm      118
Analytic representation      10
Anti-involution      116
Anti-involution of the first kind      135
Anti-involution of the second kind      135
Appell — Humbert Theorem      32
Arithmetic genus      289
Automorphism of a line bundle over a point      149
Azygetic      114
Bertini's theorem      81 290
Bidegree of a correspondence      341
Bogomolov's inequality      304
Brauer group      136
Canonical basis      47
Canonical factor (of automorphy)      32
Canonical polarization of J(C)      323
Canonical representation of the theta group      156
Canonical theta divisor      330
Canonical theta function      51
Characteristic of a line bundle      48
Characteristic polynomial of the analytic representation      117
Characteristic polynomial of the rational representation      117
Chern character      70
Chow's theorem      410
Classical factor of automorphy      51
Classical form of Riemann's Theta Relations      210
Classical theta function      52 226 227
Cocycle relation      412
Cohomology of the Poincare bundle      69
Commutator map of the theta group      154
Compatible characteristics      162
Compatible decompositions      160 162
Compatible theta structures      170
Complementary abelian subvarieties      127
Complementary abelian subvariety      127
Complex analytic space      409
Complex multiplication      268 272
Complex torus      7
Configuration, $16_{6^{-}}$       317
Congruence subgroup      222
Correspondence      340
Criterion of Matsusaka — Ran      348
Cubic equations      207
Cubic Theta Relations      202 207
Cycle, generating an abelian variety      348
d-gonal curve      390
De Franchis, Theorem of      405
Decomposition for E      50
Decomposition for H      50
Decomposition for L      48 50
Decomposition of the lattice      223
Decomposition theorem      78
Degree of a homomorphism      12
Degree of a polarization      121
Desargues configuration      210
Difference map      338
Differentiable theta function      59
Divisor, even      94
Divisor, odd      94
Dolbeault cohomology group      58
Donagi's Tetragonal Construction      393
Dual Abelian variety      73
Dual complex torus      35
Dual Jacobian Variety      361
Dual lattice      35
Elliptic curve      8
Elliptic involution      302
Endomorphism structure of a polarized abelian variety      249
Equivalence, algebraic      89
Equivalence, numerical      107 344
Equivalent correspondence's      340
Equivalent correspondences      340
Euler — Poincare characteristic      66
Even divisor      94
Even theta characteristic      331
Exceptional singularity      388
Exponent of a polarization      116
Exponent of a Prym — Tyurin variety      371
Exponent of an abelian subvariety      125
Exponent of an isogeny      12
Exponential map      7
Extended Heisenberg group      175
Extended theta group      174
Extended theta structure      175
Factor of automorphy      24 412
Fay's Trisecant Identity      356
Finite theta function      169
First Chern class      24 43
First Chern class of a line bundle      43
Fixed point free correspondence      400
Free action      411
Fundamental class      328
Fundamental system      114
Gauss map      82
Generalized Gauss map      112
Generalized level n-structure      222
Generalized Prym variety      371
Goepel tetrahedron      296
Green's operator      19
Hamiltonian quaternions      133
Harmonic form      18
Harmonic form with values in a line bundle      59
Heat equation      230
Heisenberg group      164
Hermitian form      29
Hermitian metric      17
Hermitian metric on a line bundle      59
Hilbert modular variety      256
Hodge decomposition      15
Hodge-structure of weight      1 22
Homological equivalence      107
Homomorphism      9
Homomorphism of polarized abelian varieties      72
Hyperbolic form      313
Hypotheses of the Isogeny Theorem      162
Ideal generated by forms of degree $\leq k$       194
Index of a line bundle      63
Induced polarization      72
Intersection number      78
Intersection number of cycles      106
Invariant form      14
Invariant form of type (p, q)      16
Inverse Formula      91
Inverse Formula for Finite Theta Functions      181
Irreducible principal polarization      87
Isogenous complex tori      13
Isogeny      11
Isogeny of type D      245
Isogeny Theorem      160

Isogeny Theorem for finite theta functions      171
Isomorphic polarization's      124
Isomorphic polarizations      124
Isomorphism of a line bundle over $(—1)_{X}$       90
Isomorphism of polarized abelian varieties with endomorphism structure      249
Isomorphism, associated to a theta structure      168
Iwasawa Decomposition of $S_{P_{2g}}(\mathbb{R})$       246
Jacobian (variety)      322
Kaehler manifold      17
Kaehler metric      17
Kanev's Criterion      399
Klein quartic      364
Kronecker product of matrices      248
Kummer surface      208 292
Kummer variety      98 317
Lefschetz decomposition      109
Lefschetz's theorem      86
Level D-structure      164 166 221
Level n-structure      222
Level structure      220
Maximal quotient abelian variety      112
Moduli space of polarized abelian varieties with endomorphism structure      254 261 267 272
Moving Lemma      130
Multi-index      16
Multiplication by N      172
Multiplication formula      185
Multiplication map      183
Mumford's Index Theorem      69
N-division point      12
Nakai — Moishezon criterion      79
Narasimhan — Nori theorem      144
Neron — Severi group      29 43
Nondegenerate line bundle      38
Norm, map      337
Norm-endomorphism      125
Norm-endomorphism, Criterion      126
Normalized isomorphism      91
Normalizer of the Heisenberg group      181
Normally generated line bundle      190
Numerical equivalence      107 344
Odd divisor      94
Odd theta characteristic      331
Opposite algebra      136
Orthogonal level D-structure      238
p-Cycle, algebraic      130
Pair of complementary abelian subvarieties      127
Period matrix      8
Period matrix for J(C)      322
Period of a complex torus      319
Pfaffian      52
Picard number      44 318
Picard torus      362
Poincare bundle      39
Poincare bundle of degree n for C      334
Poincare's Complete Reducibility Theorem      128
Poincare's Formula      328
Poincare's Reducibility Theorem      127
Poincare's Reducibility Theorem for Complex Tori      70
Polarization      72
Polarized Abelian variety      72
Polarized abelian variety with endomorphism structure      249
Polarized abelian variety with symplectic basis      214
Pontryagin product      21 104
Positive anti-involution      133
Positive definite line bundle      53
Positive semidefinite line bundle      57
Prime form      356
Primitive cohomology class      109
Primitive endomorphism      126
Principal congruence subgroup      223
Principal polarization      72
Projectively normal variety      190
Projectivized differential of the Abel — Jacobi map      226
Projectivized differential of the Abel — Prym map      383
Proper and discontinuous action      218 410
Proper intersection      130
Prym canonical map      384
Prym differential      384
Prym map      408
Prym variety      376
Prym — Tyurin variety      371
Prym — Tyurin variety for a curve      371
Quadratic form associated to $e^{H}$       95
Quaternion algebra      135
Radical of H      57
Rational map      102
Rational norm      118
Rational representation      10
Real Riemann matrix      111
Real torus      21
Recillas' Theorem      390
Reduced automorphism group      347
Reduced characteristic polynomial      133
Reduced pfaffian      58
Reduced trace      133
Reider's theorem      301
Riemann Relations      75
Riemann theta function      227
Riemann — Roch Theorem for vector bundles on complex tori      70
Riemann — Roch Theorem, analytic      66
Riemann — Roch theorem, geometric      67
Riemann — Roch Theorem, geometric version for curves      332
Riemann's constant      330
Riemann's Equations      202
Riemann's singularity theorem      330
Riemann's Theta Relations      201
Rigidity lemma      101
Root of a polarized abelian surface      245
Rosati (anti-)involution      116
Rosenhain tetrahedron      296
Schottky — Jung-Relation      406
Schroedinger representation      168
Seesaw Principle      412
Seesaw Theorem      411
Self-duality of the Kummer surface      295
Self-intersection number      67
Semicharacter      29
Shimura variety (analytic)      280
Siegel upper half space      214
Signature      269
Simple abelian variety      128
Singular hyperplane      317
Singular plane      293
Singularity locus of $\Theta$       331
Singularity locus of the theta divisor      331
Stable singularity      388
Stable vector bundle      304
Star-operator *      108
Stein factorization      11
Stone — von Neumann Theorem for Theta Groups      179
Symmetric divisor      93
Symmetric endomorphism      121
Symmetric idempotent      126
Symmetric line bundle      34
Symmetric theta structure      175
Symplectic basis      47
Symplectic group      215
Syzygy-module      210
Tetragonal construction      393
Theorem of de Franchis      405
Theorem of Lefschetz      85
Theorem of Serre — Rosenlicht      178
Theorem of the Cube      44
Theorem of the Square      33
Theta characteristic      330
Theta divisor      323
Theta function for a factor of automorphy      51
Theta group of L      149 152
Theta null value      236
Theta relations      200

1 2

О проекте