|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Glimm J., Jaffe A. — Quantum Physics: A Functional Integral Point of View |
|
|
 |
| Предметный указатель |
Activity estimate 405
Analyticity 68ff 90 239 240 302 304 365ff 389 390
Anharmonic oscillator 12 18 111ff 119 120
Annihilation operator 13 116 180
Anomalous dimension 78
Anomalous magnetic moment 27 308 312ff
Asymptotic completeness 23 274 275
Asymptotic field 100 273ff 281ff
asymptotic freedom 438 459
Asymptotic state 276ff
atom 7 20
Axioms 89ff
Axioms, Bethe — Salpeter 301ff
Axioms, Euclidean 89ff 296
Axioms, Haag — Kastler 97 99ff 379
Axioms, Minkowski 97ff
Axioms, Osterwalder — Schrader 90 159ff 179 225 236ff 250ff 256 265 316ff 353 379ff 393ff 461
Axioms, verification of 250ff 255ff 265ff 316ff 320ff 393ff
Axioms, Wightman 97 256
Bessel's inequality 123
Bethe — Salpeter 188 275 300ff
Bilinear forms 129ff
Bochner theorem 148ff
Bogoliubov transformation 117
Boltzmann's constant 33
Borel summability 119 350 461ff
Bose — Einstein 117
Boson 11 32 92 116 117 160 215 463 464
Bound state 11 22 23 24 115 216 273ff 277 300 302 303 340 341 342 356
boundary conditions 37 150ff 177ff 189 194 199 219 235 242 464 465 471 see "Neumann"
Boundary conditions, monotonicity in 123 165 166ff 169ff 177 179 230 231ff 249ff 251 261
Boundary conditions, periodic 163ff 179ff
Boundary conditions, weak coupling 254 348
Brownian motion 43ff
Calculus on function space 202ff
Canonical see "Ensemble"
Canonical exponent 160 349 350
Canonical quantization 111ff 296 344
Canonical, commutation relations 10 25 107 108 111 112 113 115
Canonical, coordinates 6 20 21
Casimir operator 26
Cayley's theorem 406
Channel 277
Channel, irreducible 301
Charge 20 see
Charge, density 307
Classical 6 86 see
Classical approximation 43 76
Classical critical point 78
Classical description 77
Classical differential equation 117 408
Classical exponent 349ff
Classical field 107 114
Classical force laws 28 311
Classical limit 3
Classical statistical mechanics 4 22ff
Classical trajectory 31
Cluster 23 24 68 273
Cluster, decomposition 276 277
Cluster, expansion 37ff 81 86 168 254 348 356ff 398ff 413 461 463 464 466
Cluster, property 283 286ff 359 365ff 394ff
Commutation relations 10 25 107 108 110 112 113 115
Conditioning 69 206 232 263
Configuration 82 83 84 86
Configuration, classical field 114 321
Configuration, space 114
Connected functions 286
Contraction semigroup 145
Cooperative phenomena 36 108 116
Correlation inequalities 56ff 78 81 119 200 220 225 229 417 427ff
Correlation inequalities for 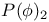 fields 229ff 339 461 fields 229ff 339 461
Coulomb 87
Coulomb force 28
Coulomb gas 465ff 469
Coulomb interactions 86 468
Coulomb potential 7 11 20 22 23
Coupling constant 43 119 215 216 218 342 411 see
Covariance operators 159ff see "Gaussian" "Boundary "Neumann"
Covariance operators in Gaussian integral, change of 208 210
Covariance operators, free 161ff
Covariance operators, lattice 219ff
Covariance operators, periodic 163ff
Creation operators 13 116 180
critical exponent 78 87 119 343 349ff 354
Critical point 30 56 73 77 78 80 118 119 160 320 339ff 345 348 353 356
Critical surface 30
Critical temperature 78 86
Cylinder, function 93 208 209 245 246
Cylinder, set 46 139ff
Defect index 127
density 28 32 35 37
Diagram see "Feynman" "Mayer"
Diagram, charge see "Vertex"
Diagram, mass 217 218
Diagram, skeleton 217
Diagram, vacuum 187
Dipole 86 87 331 469
Dirac equation 22 27 115 308ff
Dirac field 115 117
Dirac particle 312
Dirac sea 118
Dirichlet boundary conditions 37 160 161 165ff 168ff 177ff 219ff 230ff 234ff 243ff 249 264 324 339 see "Conditioning"
Dirichlet covariance 167ff 173ff 247 248
Dirichlet data 168 244 246ff
Dirichlet difference Laplacian 220
Dirichlet limit 209
Dirichlet monotonicity 230 231ff
distribution 53 75 89 90
Droplet model 81ff
Duplicate variable 57 59 60 64 65 67 72 366
Dyson equation 297ff
Electromagnetism 11 20 306ff
Energy 7 8 30 31 32 34 39 94ff
Energy-entropy bounds 405 421
Ensemble 30ff
Ensemble, Canonical 32ff
Ensemble, Grand Canonical 34ff 37ff 465ff 468ff
Ensemble, microcanonical 31ff
entropy 32 34 77 84 322
Entropy, estimate 405
Equation of motion 219ff see
Equilibrium 37
Equilibrium state 28ff 31ff 60
Ergodic 31 74 86 90 92 96 393ff
Essential self-adjointness 126 127
Euclidean see "Axiom" "Field" "Functional
Euclidean propagator see "Covariance operators"
Existence of quantum fields 157 250ff 271 359ff
Fermi field 160 462 463
Fermi — Dirac 115 117
Fermion 11 32 115ff 463 464
Ferromagnetic interaction 57ff 59 60 66 69 71 72 200ff 220 330
Feynman 43 44
Feynman — Kac formula 13 43ff 47ff 52ff 89 93 112 114 115 142 144 172 241 244 246 382ff 462 463
Feynman, graph, diagram 138 158 180ff 186 187 189 213 214 217 299 313
Field, Euclidean 89ff
Field, Minkowski 97ff
Field, strength renormalization 436
Field, theory 89ff
Fine structure 308 314 315
Fine structure constant 24 219 313
FKG (Fortuin — Kastelyn — Ginibre) inequality 64ff 229 317 318 319
Fock, representation 107ff
Fock, space 106 108 115ff 243 273 274 275
Fock, vacuum 281
Free energy 33 34 65 66 68ff 230 231ff 254 273 407 412ff
Free field 100ff 106ff 111ff 159ff 273 274 282 283 287 295 343 365 see
Friedrichs extension 129 131
Fugacity 35 65
Functional 92ff 202ff
| Functional derivative 202ff
Functional determinant 206ff 211ff see
Functional integral 47ff 52ff 89ff
Gauge field 120 410
Gauge fixing 440 441 452 453 455
Gauge theory 87 409 410 437ff
Gaussian see "Covariance operators" "Free "Integration
Gaussian critical point 119
Gaussian field 105
Gaussian functional 100 205 234
Gaussian functional integral of measure 49 90 100ff 106ff 111ff 180ff 183ff 186 188ff 205ff 208 209 211 226ff 235 243ff 253 357 360 366 460 466
Gaussian inequalities 428 432
Gaussian measure, translation of a 207
Gaussian measures 136ff
Gaussian process 119 226
Generating functional 53 55 90 101 102 104 105
Gibbs 31 34 356 357
Graph convergence 169
Green's function 159 161 255 332 333 342 see "Covariance "Dirichlet" "Neumann"
Griffiths inequalities 56 59 64 72 229 340 346 349 352 417
Ground state see "State" "Phase"
Ground state, classical 75ff 85
Ground state, nonuniqueness of 73ff 78ff 81ff 320ff 393ff 422ff see
Ground state, quantum 11 13 19 25 51 85 93 95 113 115 310 see
Ground state, uniqueness of 50ff 74ff 86 97 340ff 356 359 393ff see
Haag — Kastler axioms 97 99 264 265 286 379 393 464
Haag — Ruelle scattering 274 275 286ff
Hamilton's equations 4ff
Hamiltonian 4 12ff 57ff 110ff
harmonic oscillator 12ff 106 111 112 119 189 244 246
Heat bath 32 33
Heat equation 44 288 see
Heat kernel 423
Heisenberg ferromagnet 37
Heisenberg model 235 330 331
Heisenberg picture 6 8 9 10
Helium atom 23
Hermite expansion 108
Hermite function 12 14 17
Hermite polynomials 14 15 106 109 180 189 204 206
Hermite recursion relation 185
Hierarchical model 79
Higgs 317 330
Higgs model 439 444
Hilbert space 122ff
Hoelder continuity 142 143
Hohenberg — Mermin — Wagner theorem 331
Hydrogen atom 11 20 23 24ff 314 315
Hydrogen atom, hyperfine structure 314 315
Ideal gas 29 35 37 77
Image charges 164 165
Index theorem 437
Infinite volume limit 56 59ff 229ff 249ff 255ff 337ff 463
Infra-red behavior 451ff
Instanton 37 470 471
Integration by parts 106ff 207ff 255 256ff 423 424
Ising limit 68 70 355
Ising model 36ff 59 66 69 70 73ff 81ff 119 235 320 341 349 351 412 416 470
Ising phase transition 73ff 81ff
Kirkwood — Salsburg equations 360ff 364
Klein — Gordon equation 115 283ff
Kosterlitz — Thouless transition 86ff
Lagrangian 44 215
Lamb shift 27 315ff
Lattice, approximation 118 209 219ff 225ff 442ff 446ff 454ff
Lattice, approximation, convergence of 209 222 227ff
Lattice, covariance operators 179 219ff
Lattice, fields 36ff 60 68ff 79 96 118 234ff
Lattice, Laplace operators 36 219ff
Lebowitz inequality 22 61 230 348 349 431
Lee — Yang theorem 56ff 65ff 81 229 230 336 339
Legendre transformation 34 36 44 188
Lehmann spectral formula 102 298 342 350
Lehmann — Symanzik — Zimmerman 275 295
Lennard — Jones potential 23 28
Lie product theorem 144ff
Linked cluster expansion 403
Liouville's theorem 5 31
Local stopping times 421ff
Locality 98 99 392ff
Lorentz covariance 92 98 100 309 389ff
Lorentz group 98 115 116 280 281
Magnetic dipole force 28
Magnetic field 65 310
Magnetic moment of electron 326ff
magnetization 80 81 306 319 336 340
Mass 20
Mass, center of 20 22 24 276 277 306
Mass, gap 287ff 359ff
Mass, operator 303 345
Mass, reduced 21
Mass, shift 206ff 211ff 216ff
Mass, skeleton 218
Mass, spectrum 274ff 300ff 356ff 461
Mayer graphs 40 357
Mayer series 38 41 76
mean field 70 75 79 85 86ff 330 349 356 465ff 467 469 470
Mehler's formula 19 48 244 246
Mermin — Wagner theorem 86 87 331
Microcanonical see "Ensemble"
Minkowski see "Axioms field"
Minlos' theorem 53 54 148ff
Moebius' theorem 286
Momentum cutoff 188 191 259 460ff see
Momentum scale 448
Monotonicity see "Boundary conditions" "Conditioning" "Dirichlet" "Neumann"
Multiple reflection see "Reflection"
Neumann see "Boundary conditions" "Conditioning"
Neumann boundary conditions 159ff 164 177 178 230ff 253
Neumann covariance 164ff 327
Neumann limit 209
Neumann monotonicity 231ff
Neumann series 128
Non-Gaussian path space measures 52ff 193ff 248ff
Noninteraction theorem 433ff
Nuclear space 132ff
Observable 3ff 8 31 98 99 148 394
One particle irreducible 217
Operator, bounded 122
Operator, unbounded 122
Order parameter 80
Ornstein — Uhlenbeck 49 137
Osterwalder — Schrader 90 159ff 179 225 358 see "Reflection
Parallel transport 87 443ff 449
Particle, interpretation 273ff 280ff 286ff 300ff
Particle, reservoir 35
Partition function 33 57 66 68 69 81 212 231 243 263 298 327 360 367 370 465 466 468
Path 44 45 47
Path, space 48ff 52 93 157 168 182 239 462 see
Path, splitting 429ff
Pauli exclusion principle 11 23 28 151
Pauli matrices 312
Peierls' argument 82ff 321ff
Peierls' expansion 416
Perron — Frobenius theorem 51
Perturbation theory 43 186ff 255 296 297ff 313 461
Phase 73ff 79ff 81 82 99 316 317
Phase transition 30 38 56 65 66 70 72ff 73ff 99 119 199 316ff 330 333 339 348 378 461ff 469 470 471
Phase transition with no change in symmetry group 79 86 465
Phase transition with symmetry breaking 79ff 81ff 320ff 333ff
Phase transition, first order 81 317
Phase transition, higher order 320
Phase transition, proof of existence 81ff 320ff 333ff
Phase, boundary 82ff 321ff 400 416ff 464
Phase, cell localization 437ff 447ff
Phase, diagram 70 465
Phase, disordered 87
Phase, mixed 73ff
Phase, multiple 81ff 320ff 335 461 464ff
Phase, pure 73ff 79ff 99 316ff 335 339 356 464
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



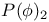 fields
fields