|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Faddeev L.D., Takhtajan L., Reyman A.G. — Hamiltonian methods in the theory of solitons |
|
|
 |
| Предметный указатель |
 -soliton solution 135 171 383 429 497-498 -soliton solution 135 171 383 429 497-498
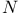 -wave model 309 -wave model 309
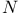 -wave model, -wave model,  -matrix for 466 -matrix for 466
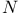 -wave model, equation of 310 -wave model, equation of 310
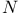 -wave model, Hamiltonian for 311 -wave model, Hamiltonian for 311
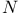 -wave model, Poisson structure of 311 -wave model, Poisson structure of 311
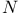 -wave model, zero curvature condition for 309-310 -wave model, zero curvature condition for 309-310
 -matrix 189 528 -matrix 189 528
 -matrix, elliptic 537 -matrix, elliptic 537
 -matrix, rational 533 -matrix, rational 533
 -matrix, trigonometric 536 -matrix, trigonometric 536
 -matrixfor the -matrixfor the 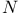 -wave model 466 -wave model 466
 -matrixfor the HM model 386 -matrixfor the HM model 386
 -matrixfor the KdV model 467 -matrixfor the KdV model 467
 -matrixfor the LHM model 516 -matrixfor the LHM model 516
 -matrixfor the LL model 458 -matrixfor the LL model 458
 -matrixfor the LLL model 508 -matrixfor the LLL model 508
 -matrixfor the LSG model 517 -matrixfor the LSG model 517
 -matrixfor the NS model 189 -matrixfor the NS model 189
 -matrixfor the NS model, vector 466 -matrixfor the NS model, vector 466
 -matrixfor the SG model 433 -matrixfor the SG model 433
 -matrixfor the Toda model 473 -matrixfor the Toda model 473
 -matrixfor the Toda model, two-dimensional 467 -matrixfor the Toda model, two-dimensional 467
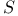 -matrix, classical 246 393 444 -matrix, classical 246 393 444
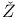 ukowsky function 68 ukowsky function 68
 -ordered matrix exponential 23 -ordered matrix exponential 23
 -operator 212 270 562 -operator 212 270 562
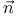 -field equation 328 -field equation 328
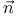 -field equation, Hamiltonian for 328 -field equation, Hamiltonian for 328
Action for chiral field 312 322
Action for chiral field, modified 331
Action-angle variables finite density 253-258
Action-angle variables fortheHM model 338
Action-angle variables fortheNS model,rapidlydecreasing 229-232
Action-angle variables fortheSG model 435-437
Action-angle variables fortheToda model 503
Algebra of observables 13
Annihilator 20 325-326 510 524
Auxiliary linear problem 23 533
Auxiliary linear problem for continuous models 306-307
Auxiliary linear problem for lattice models 293
Auxiliary linear problem for the 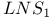 model 302 model 302
Auxiliary linear problem for the chiral field model 312
Auxiliary linear problem for the HM model 356
Auxiliary linear problem for the KdV model 308
Auxiliary linear problem for the LHM model 297
Auxiliary linear problem for the LL model 287
Auxiliary linear problem for the LLL model 511
Auxiliary linear problem for the NS model 23
Auxiliary linear problem for the SG model 393
Auxiliary linear problem for the SG model in light-cone variables 450
Auxiliary linear problem for the Toda model 475
Auxiliary linear problem, reflectionless 126
Auxiliary space 288 528
Averaging of fundamental Poisson brackets 538-539
Averaging of fundamental Poisson brackets of an  -matrix 533-538 -matrix 533-538
Averaging of fundamental Poisson brackets on the lattice 542
Blaschke factor 50
Blaschke — Potapov matrix factor 92 380 426
boundary conditions 11
Boundary conditions, finite density 12 294
Boundary conditions, periodic 284
Boundary conditions, quasi-periodic 12 282 289 294
Boundary conditions, rapidly decreasing 11 282 285 294
Boundary conditionsin the sense of Schwartz 12
Breather 428
Brillouin zone 262 390
Canonically conjugate variables 230
Cartan — Weyl basis 466
Casimir function 524 529 544 552
Central extension 333 548
Charge 16
Chiral field equation 31 1
Chiral field equation, modified 331
Chiral field model 311-313 321-333
Chiral field model on a homogeneous space 313
Chiral field model, action for 312 322
Chiral field model, admissible functional for 326
Chiral field model, auxiliary linear problem for 312
Chiral field model, boundary conditions for 324 326
Chiral field model, Hamiltonian for 323 328
Chiral field model, modified 331-333
Chiral field model, Poisson structure of 322-329 332-333
Chiral field model, Poisson structure of, annihilator of 325-326
Chiral field model, principal 311-312
Chiral field model, zero curvature condition for 312
Coadjoint action 524 553
Cocycle 323 333 548
Compatibility condition 20
Condensation of zeros for the HM model 391
Condensation of zeros for the NS model 246-247
Condensation of zeros for the SG model 439
Condition (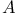 ) 49 362 400 ) 49 362 400
Condition (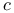 ) 485 ) 485
Condition ( ) 69 149 254 ) 69 149 254
Condition for the determination of signs 71 485
Conjugation problem 114-115 146-148
Connection coefficients 21
Conservation law 23
Continuous spectrum 49 56 477
continuum limit 298
Coupling constant 11
Current algebra 323 524
Current algebra, central extension of 333 548
Currents, left 311
Currents, right 323
Derivation property 188
Discrete spectrum 49 65 363 400-401 483
Dispersion law 243 262 390 438
Dispersion relation for the HM model 363
Dispersion relation for the NS model, finite density 68
Dispersion relation for the NS model, rapidly decreasing 51
Dispersion relation for the SG model 401
Dispersion relation for the Toda model 484
Divisor 334
Double soliton 428
Dressing procedure 336 555-558
Energy integral 16
Evolution equations for the Jost solutions 52 72 364 402 486
Evolution equations for the reduced monodromy matrix 52 73 364 402 487
Evolution equations for the transition coefficients 53 73 364 403 452 487
Evolution equations for the transition matrix 29 72 402 486
Evolution equations of Heisenberg type 29
Factorization of scattering 136 177 393 431
Factorization problem 546 552 559-560
Finite-gap solutions 268
Functional, admissible 18 75 209 235 237 239 326 369 499 505
Functional, inadmissible 19 260 283 369 390 505
Functional, local 33-34 364 487
Functional, multi-valued 292 330
Functional, real-analytic 13
Functional, smooth 13
Functional, with compact support 18 186
Fundamental Poisson brackets for the HM model 385-386
Fundamental Poisson brackets forlattice models 508
Fundamental Poisson brackets fortheLL model 458
Fundamental Poisson brackets fortheNS model 189
Fundamental Poisson brackets fortheSG model 433
Gap 57
Gauge equivalence 306 315
Gauge transformation 22 34 306 550
Gelfand — Levitan — Marchenko equation for the HM model 375
Gelfand — Levitan — Marchenko equation for the NS model, rapidly decreasing 116-117
Gelfand — Levitan — Marchenko equation for the NS model, rapidly decreasing, finite density 152-153
Gelfand — Levitan — Marchenko equationfor the Toda model 491
Gelfand — Levitan — Marchenko equationfor theSG model 416-417
Generating function for integrals of the motion 345
Generating function for integrals of the motion for the HM model 368
Generating function for integrals of the motion for the NS model 25 33-38 54 73
Generating function for integrals of the motion for the SG model 406
| Generating function for integrals of the motion for the Toda model 487-488
Generating function of canonical transformation for soliton scattering for the HM model 392 393
Generating function of canonical transformation for soliton scattering for the NS model 244 245
Generating function of canonical transformation for soliton scattering for the SG model 444-445
Gohberg — Krein theorem 90
Goursat problem for the kernels 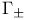 359 397 359 397
Hamiltonian 15
Hamiltonian for the 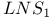 model 301 model 301
Hamiltonian for the 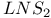 model 304 model 304
Hamiltonian for the 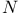 -wave model 311 -wave model 311
Hamiltonian for the 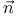 -field model 328 -field model 328
Hamiltonian for the chiral field model 323 328
Hamiltonian for the chiral field model, modified 332
Hamiltonian for the HM model 283 390
Hamiltonian for the KdV model 309
Hamiltonian for the LHM model 296
Hamiltonian for the LL model 287
Hamiltonian for the LLL model 513
Hamiltonian for the LSG model 517
Hamiltonian for the NS model 16 19
Hamiltonian for the NS model, vector 288
Hamiltonian for the SG model 285
Hamiltonian for the SG model in light-cone variables 448
Hamiltonian for the Toda model 294
Hamiltonian for the Toda model, two-dimensional 313
Hamiltonian for the Volterra model 295
Hamilton’s equations of motion 15 545 551
Heisenberg magnet (HM) equation 281
Heisenberg magnet (HM) equation, higher 389
Heisenberg magnet (HM) model 281
Heisenberg magnet (HM) model,  -soliton solution for 383 -soliton solution for 383
Heisenberg magnet (HM) model,  -matrix for 386 387 -matrix for 386 387
Heisenberg magnet (HM) model, action-angle variables for 388
Heisenberg magnet (HM) model, admissible functional for 369
Heisenberg magnet (HM) model, auxiliary linear problem for 356
Heisenberg magnet (HM) model, boundary conditions for 282
Heisenberg magnet (HM) model, canonical variables for 388
Heisenberg magnet (HM) model, complete integrability of 388-389
Heisenberg magnet (HM) model, condition (A) for 362
Heisenberg magnet (HM) model, discrete spectrum in 363
Heisenberg magnet (HM) model, dispersion law for 390
Heisenberg magnet (HM) model, dispersion relations for 363
Heisenberg magnet (HM) model, fundamental Poisson brackets for 385-386
Heisenberg magnet (HM) model, gauge transformation of 315-321 391
Heisenberg magnet (HM) model, Gelfand — Levitan — Marchenko equation for 375
Heisenberg magnet (HM) model, Hamiltonian for 283 390
Heisenberg magnet (HM) model, higher equations for 389
Heisenberg magnet (HM) model, inadmissible functional for 283 369
Heisenberg magnet (HM) model, integrals of the motion for 366-368
Heisenberg magnet (HM) model, integrals of the motion for, generating function for 368
Heisenberg magnet (HM) model, interaction of solitons in 384
Heisenberg magnet (HM) model, inverse scattering problem for 370 372-373
Heisenberg magnet (HM) model, Jost solutions for 358
Heisenberg magnet (HM) model, Jost solutions for, analytic properties of 360
Heisenberg magnet (HM) model, Jost solutions for, asymptotic behaviour of 358 360-361
Heisenberg magnet (HM) model, Jost solutions for, evolution equations for 364
Heisenberg magnet (HM) model, Jost solutions for, integral equations for 359
Heisenberg magnet (HM) model, Jost solutions for, involutions for 358
Heisenberg magnet (HM) model, Jost solutions for, Poisson brackets of 386
Heisenberg magnet (HM) model, momentum for 283 292 320 390
Heisenberg magnet (HM) model, monodromy matrix for, reduced 361
Heisenberg magnet (HM) model, Poisson structure of 282 391
Heisenberg magnet (HM) model, Riccati equation for 365
Heisenberg magnet (HM) model, Riemann problem for 370-372
Heisenberg magnet (HM) model, scattering of solitons in 384 392-393
Heisenberg magnet (HM) model, scattering transformation for 393
Heisenberg magnet (HM) model, soliton for 379-381
Heisenberg magnet (HM) model, spin for 283 368-369 390
Heisenberg magnet (HM) model, trace identities for 368
Heisenberg magnet (HM) model, transition coefficients for 361
Heisenberg magnet (HM) model, transition coefficients for, analytic properties of 362-363
Heisenberg magnet (HM) model, transition coefficients for, asymptotic expansion of 368
Heisenberg magnet (HM) model, transition coefficients for, evolution of 364
Heisenberg magnet (HM) model, transition coefficients for, normalization condition for 361
Heisenberg magnet (HM) model, transition coefficients for, Poisson brackets of 387-388
Heisenberg magnet (HM) model, transition matrix for 357
Heisenberg magnet (HM) model, transition matrix for, asymptotic expansion of 364-365
Heisenberg magnet (HM) model, transition matrix for, involution for 358
Heisenberg magnet (HM) model, transition matrix for, Poisson brackets of 386
Heisenberg magnet (HM) model, zero curvature condition for 284 315
Hierarchy of Poisson structures 217-218 563-565
Hopf bundle 320
Integrability 307
Integral equations for the Jost solutions 44 359
Integral equations for the kernels  , , 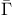 31 31
Integral equations for the transition matrix 30
Integral of the motion 16
Integral of the motion for the HM model 366-368
Integral of the motion for the LLL model 512 514
Integral of the motion for the NS model, finite density 73-76
Integral of the motion for the NS model, rapidly decreasing 53
Integral of the motion for the SG model 403-407
Integral of the motion for the SG model in light-cone variables 452 463
Integral of the motion for the Toda model 474 487-489
Integral of the motion in involution 17
Integral of the motion, local 33 364 512
Integral representations for 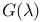 , , 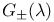 85 86 140 144-145 85 86 140 144-145
Integral representations for 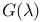 , , 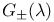 for Jost solutions 41 57 359 397 for Jost solutions 41 57 359 397
Integral representations for 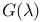 , , 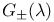 for monodromy matrix 32 47 64 for monodromy matrix 32 47 64
Involutions for 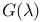 , , 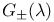 84 86 140 141 371 408-409 84 86 140 141 371 408-409
Involutions for 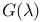 , , 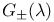 for Jost solutions 41 43 59 61 358 396 478 for Jost solutions 41 43 59 61 358 396 478
Involutions for 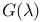 , , 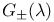 for monodromy matrix 45 62 361 399 481 for monodromy matrix 45 62 361 399 481
Involutions for 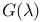 , , 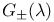 for transition matrix 28 358 394-396 for transition matrix 28 358 394-396
Jacobi identity 14 188
Jacobi matrix 479
Jost solutions for the HM model 358
Jost solutions for the NS model, finite density 57-58
Jost solutions for the NS model, rapidly decreasing 42
Jost solutions for the SG model 396
Jost solutions for the Toda model 477
Kadomtsev — Petviashvili equation 350
Killing form 321 527
Korteweg-de Vries (KdV) equation 307
Korteweg-de Vries (KdV) model 307
Korteweg-de Vries (KdV) model,  -matrix for 467 -matrix for 467
Korteweg-de Vries (KdV) model, auxiliary linear problem for 308
Korteweg-de Vries (KdV) model, Hamiltonian for 309
Korteweg-de Vries (KdV) model, momentum for 309
Korteweg-de Vries (KdV) model, Poisson structure of 308
Korteweg-de Vries (KdV) model, zero curvature representation for 307-308
Landau — Lifshitz (LL) equation 287
Landau — Lifshitz (LL) model 286 457
Landau — Lifshitz (LL) model,  -matrix for 458 -matrix for 458
Landau — Lifshitz (LL) model, auxiliary linear problem for 287
Landau — Lifshitz (LL) model, boundary conditions for 282
Landau — Lifshitz (LL) model, Hamiltonian for 287
Landau — Lifshitz (LL) model, limiting cases of 459-462
Landau — Lifshitz (LL) model, momentum for 292
Landau — Lifshitz (LL) model, Poisson structure of 458
Landau — Lifshitz (LL) model, zero curvature representation for 287 457
Lattice Heisenberg magnet (LHM) equation 296
Lattice Heisenberg magnet (LHM) model 296
Lattice Heisenberg magnet (LHM) model,  -matrix for 516 -matrix for 516
Lattice Heisenberg magnet (LHM) model, auxiliary linear problem for 297
Lattice Heisenberg magnet (LHM) model, boundary conditions for 296
Lattice Heisenberg magnet (LHM) model, continuum limit of 298
Lattice Heisenberg magnet (LHM) model, Hamiltonian for 296
Lattice Heisenberg magnet (LHM) model, partially anisotropic 516
Lattice Heisenberg magnet (LHM) model, Poisson structure of 296
Lattice Heisenberg magnet (LHM) model, zero curvature condition for 297
Lattice Landau — Lifshitz (LLL) model 508-515
Lattice Landau — Lifshitz (LLL) model, ,  -matrix for 508 -matrix for 508
Lattice Landau — Lifshitz (LLL) model, ,zero curvature condition for 514
Lattice Landau — Lifshitz (LLL) model, annihilator for 510
Lattice Landau — Lifshitz (LLL) model, auxiliary linear problem for 511
Lattice Landau — Lifshitz (LLL) model, continuum limit of 515
Lattice Landau — Lifshitz (LLL) model, fundamental Poisson brackets for 508
Lattice Landau — Lifshitz (LLL) model, Hamiltonian for 513
Lattice Landau — Lifshitz (LLL) model, integrals of the motion for 512 514
Lattice Landau — Lifshitz (LLL) model, limiting cases of 515-518
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -soliton solution
-soliton solution  -wave model
-wave model  -matrix for
-matrix for 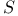 -matrix, classical
-matrix, classical 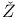 ukowsky function
ukowsky function  -ordered matrix exponential
-ordered matrix exponential  -operator
-operator 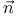 -field equation
-field equation 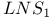 model
model 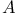 )
) 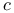 )
)  )
) 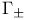
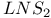 model
model  ,
, 
 ,
,