В рациональную алгебру когомологии пространства вводятся новая алгебраическая структура - структура коммутативной
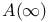
-алгебры. Показано, что алгебра когомологии , оснащенная этой структурой, является полным гомотопическим инвариантом на категории 1-связных рациональных пространств, более того, множество всевозможных коммутативных
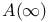
-структур на заданной 1-связной градуированной-алгебре классифицирует множество рациональных гомотопических типов с заданной алгеброй когомологии. Даны некоторые приложения этой классификации! приведен критерий формальности пространства! критерий реализуемости гомоморфизма рациональных алгебр когомологий8 построен цепной комплекс, дающий рациональные гомотопические группы.
 |
|
О проекте
|
|
О проекте

![Кадеишвили Т.В. — Структура [$]A(\infty)[$] алгебры в когомологиях и рациональный гомотопический тип](/covers/default.gif)
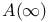 -алгебры. Показано, что алгебра когомологии , оснащенная этой структурой, является полным гомотопическим инвариантом на категории 1-связных рациональных пространств, более того, множество всевозможных коммутативных
-алгебры. Показано, что алгебра когомологии , оснащенная этой структурой, является полным гомотопическим инвариантом на категории 1-связных рациональных пространств, более того, множество всевозможных коммутативных 