Авторизация
Поиск по указателям
Morrey C. — Multiple integrals in the calculus of variations
Обсудите книгу на научном форуме Нашли опечатку?
Название: Multiple integrals in the calculus of variationsАвтор: Morrey C. Аннотация: From the reviews: "…the book contains a wealth of material essential to the researcher concerned with multiple integral variational problems and with elliptic partial differential equations. The book not only reports the researches of the author but also the contributions of his contemporaries in the same and related fields. The book undoubtedly will become a standard reference for researchers in these areas. …The book is addressed mainly to mature mathematical analysts. However, any student of analysis will be greatly rewarded by a careful study of this book."
M. R. Hestenes in Journal of Optimization Theory and Applications
"The work intertwines in masterly fashion results of classical analysis, topology, and the theory of manifolds and thus presents a comprehensive treatise of the theory of multiple integral variational problems."
L. Schmetterer in Monatshefte f?r Mathematik
"The book is very clearly exposed and contains the last modern theory in this domain. A comprehensive bibliography ends the book."
M. Coroi-Nedeleu in Revue Roumaine de Math?matiques Pures et Appliqu?es
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1966Количество страниц: 506Добавлена в каталог: 21.02.2014Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
374 380 373 380 322 320 Admissible boundary coordinate system 300 Admissible coordinate system 300 Admissible measure 489 Algebraic boundary b(X, A) 411 Area integral 1 Basis (for complex 1 forms) 331 Basis, orthogonal 332 Boundary b M of M 300 Boundary operator 319 Boundary values 76 Bounded slope condition 98 Calderon — Zygmund inequalities 56 58 Calderon's extension theorem 74 Cauchy inequality 35 Class 411 Closed forms 299 Coerciveness inequality 253 Complementing condition 212 Complex Dirichlet integral 320 Complex improper integral 174 Complex-analytic manifold 317 Contractible 414 Convex function 21 Convex set 21 Cover (in the sence of Vitali) 409 Dini condition 54 Direct methods 16 Dirichlet data 252 Dirichlet growth condition 32 Dirichlet growth lemma 79 Dirichlet integral 1 Dirichlet integral for forms 291 320 Dirichlet's principle 5 Dirtchlet problem 44 Distance 439 Distance between Erechet varieties 351 Distance between mappings [D(z1,z2)] 350 Distance geodesic 378 Distance point set 406 Distribution derivatives 20 Domain 181 Domain 174 Domain 181 Domain Lipschitz (of class 25 77 Domain of class 4 Domain of class 384 Domain strongly Lipschitz 72 Domain with regular boundary 72 Elementary function 43 Elliptic systems (of differential equations) 210 Euler's equations 2 7 8 Exterior co-differential 290 Exterior derivative 290 Exterior differential r-forms 288 Extremal 32 Federer's convergence property 492 Federer's multiplicity function 480 Field of extremals 14 First differential 31 First variation 7 8 Form, closed 299 Form, closed, 299 Form, closed, complex, of type (p,q) 318 Form, closed, even 288 Form, closed, exterior differential 288 Form, closed, in 288 Form, closed, normal part of a 301 302 Form, closed, odd 288 Form, potential of a 295 314 Form, tangential part of a 301 302 Frechet variety 351 Frechet variety on a manifold 379 Frechet variety oriented 353 Friedrichs mollifier 20 Function, absolutely continuous in the sense of Tonelli 19 67 Function, admissible 8 Function, essentially homogeneous of degree p 47 Function, mollified 20 Function, monotone in the sense of Lebesgue 16 17 Function, of class 4 Function, of class 20 Function, quasi-convex 112 Function, strongly in 114 Function, strongly quasi-convex 114 Gaffney-garding inequality 293 Garding’s inequality 253 Generalized derivatives 62 Generalized surface 354 Geodesic cones C(P,S), C( 409 410 Geodesic k-plane 406 Geodesic k-plane centered at P 406 Gradient, 1 Green's function 44 Harmonic field 294 Harmonic form 316 Harmonic function 40 Hausdorff outer measure 350 408 Hermitean metric 317 Hilbert transform 55 Hilbert's invariant integral 14 Hoelder condition 4 Hopf's extension theorem 482 483 Inner product, 333 Inner product, 320 Inner product, localized (of forms) 302 Inner product, of complex forms 319 Inner product, of complex forms, localized 319 Inner product, of forms in 289 Inner product, of forms in 2 288 Integral in parametric form 2 349 Integrals over oriented Frechet varieties 353 Integrand, normal 92 Integrand, normal of a parametric problem 349 Integrand, of type I 96 Integrand, of type II 97 Jacobi condition 15 Jacobi's equation 13 Jensen's inequality 21 Kodaira decomposition 286 298 312 322 Laplace's equation 43 Lebesgue area of a Frechet surface 352 Legendre condition 2 10 Legendre — Hadamard condition 11 Linear functionals on 70 Linear sets 312 Lipschitz condition 4 Lipschitz convergence 113 Lipschitz domain (of class 25 Localized inner product 301 Localized inner product of complex forms 319 Manifold with boundary (of class 300 Mapping, 453 Mapping, 454 Mapping, 454 Mapping, abcolutely continious 379 382 Mapping, light 489 Mapping, monotone 489 Mapping, of class 382 Mapping, of class 379 Maximum principle 40 61 Mean value properties of harmonic functions 40 41 Measurable mappings 378 Minimizing sequences 16 Minimum conditions (on a general elliptic system) 215 Minus potential (of a form) 310 Multinomial coefficient 63 n-th gradient 4 Norm 338 Norm 337 Norm 342 Normal coordinate system 402 Normal coordinate system centered at a point q on 402 Normal part (of a form) 301 302 Operator 320 Operator 319 Operator b, for complex forms 319 Operator L, for complex forms 321 Operator N, for complex forms 321 Order 0[z, 356 357 359 480 Oriented Frechet variety 353 Orthogonal basis 332 Parallel geodesic planes 443 Parametric representation 351 Plus potential (of a form) 310 Poincare’s inequality 69 Point set distance D( 406 Poisson’s equation 47 Poisson’s integral formula 45 46 Polyhedral cone 460 Potential 47 Potential of a form 259 314 Principal part (of a differential operator) 210 Problem of Plateau in 375 376 Projection 485 Projection on a geodesic p-plane 435 Properly elliptic system 211 Quasi-linear equations 8 Quasi-potential 86 Reflection principle 54 Regular mapping 64 Regular parametric problem 32 Regular Variational problem 8 11 Reifenberg cone inequality 459 460 Reifenberg's ( 433 Rellich's theorem 75 Riemannian manifold of class 288 Root condition 211 Second variation 10 Set (S, 406 Sets 453 Simplicial cone 460 Singular integrals 50 Slope functions 14 Sobolev lemmas 78 80 Sobolev spaces 19 20 Sobolev’s embedding theorem 80 Space 20 288 Space 68 Space 378 Space 318 Space 319 Space 378 Space 320 Space 320 Space 21 Space 321 Space 321 Space 343 Space 319 Space 288 Spherical harmonics 73 474 Stokes' theorem 290 Strong relative minimum 12 Strongly elliptic system 252 Strongly Lipschitz domain 72 Strongly pseudo-convex boundary 318 Supplementary conditions 211 Tangential coordinate system 321 Tangential part (of a form) 301 302 Topological type (of a Frechet variety) 351 Transversality conditions 2 Uniformly elliptic system 211 Weak convergence in 70 Weak convergence of maps in 385 Weak solutions 33 Weakly differentiable functions 97 Weierstrass condition 2 12 Weierstrass E-function 12 Weyl’s lemma 41 42
Реклама
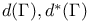
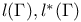
cohomology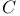 
(A, L) 
(d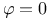
) 
) 
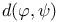
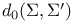
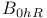
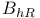
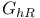
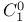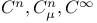, analytic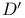 
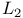-flat 
, 
, 
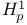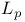
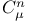
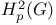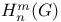
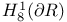
,S)
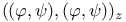
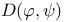
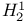
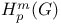
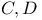
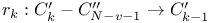
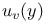
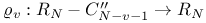
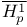
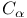
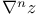
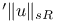
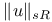
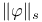for complex forms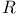 
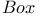, for complex forms 
] 
, 
) 
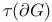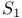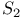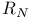
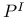
, R1) condition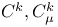 
) 
, 
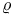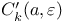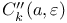
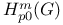
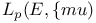(of mappings)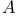 
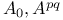
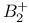and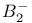 
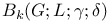
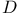, of complex forms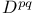 
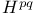
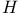of complex harmonic fields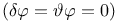 
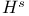
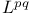, L 
|
|
О проекте