|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Apostol T.M. — Modular Functions and Dirichlet Series in Number Theory |
|
|
 |
| Предметный указатель |
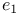 , , 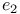 , , 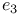 13 13
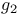 , , 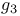 12 12
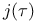 , , 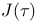 74 15 74 15
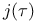 , , 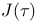 , Fourier coefficients of 21 , Fourier coefficients of 21
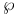 -function of Weierstrass 10 -function of Weierstrass 10
Abscissa, of absolute convergence 165
Abscissa, of convergence 165
Additive number theory 1
Apostol, Tom M. 196
Approximation theorem of Dirichlet 143
Approximation theorem of Kronecker 148 150 154
Approximation theorem of Liouville 146
Asymptotic formula for p(n) 94 104
Atkin, A.O.L. 91 196
Automorphic function 79
Basis for sequence of exponents 166
Bernoulli numbers 132
Bernoulli polynomials 54
Berwick, W.E.H. 22
Bessel functions 109
Bohr function of a Dirichlet series 168
Bohr matrix 167
Bohr, equivalence theorem 178
Bohr, Harald 161 196
Circle method 96
Class number of quadratic form 45
Congruence properties of Dedekind sums 64
Congruence properties, of coefficients of 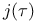 22 90 22 90
Congruence subgroup 75
Cusp form 114
Davenport, Harold 136
Dedekind function 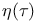 47 47
Dedekind sums 52 61
Dedekind, Richard 47
Deligne, Pierre 136 140 196
Differential equation for 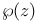 11 11
Dirichlet L-function 184
Dirichlet series 161
Dirichlet, Peter Gustav Lejeune 143
Dirichlet’s approximation theorem 143
Discriminant 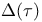 14 14
Divisor functions 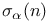 20 20
Doubly periodic functions 2
Eigenvalues of Hecke operators 129
Eisenstein series 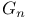 12 12
Eisenstein series 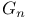 , recursion formula for 13 , recursion formula for 13
Elliptic functions 4
Entire modular forms 114
Equivalence of general Dirichlet series 173
Equivalence of ordinary Dirichlet series 174
Equivalence of pairs of periods 4
Equivalence of points in the upper half-plane H 30
Equivalence of quadratic forms 45
Estimates for coefficients of modular forms 134
Euler products of Dirichlet series 136
Euler, Leonhard 94
Exponents of a general Dirichlet series 161
Farey fractions 98
Ford circles 99
Ford, L.R. 99 196
Fourier coefficients of 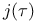 21 74 21 74
Fourier coefficients of 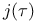 , divisibility properties of 22 74 91 , divisibility properties of 22 74 91
Functional equation, for 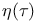 48 52 48 52
Functional equation, for 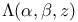 54 54
Functional equation, for 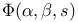 56 71 56 71
Functional equation, for 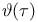 91 91
Functional equation, for  140 140
Fundamental pairs of periods 2
Fundamental region of subgroup 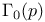 76 76
Fundamental region, of modular group  31 31
General Dirichlet series 161
Generators of congruence subgroup 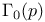 78 78
Generators, of modular group  28 28
Grosswald, Emil 61 198
Gupta, Hansraj 111 196
Half-plane H 14
Half-plane of absolute convergence 165
Half-plane of convergence 165
Hardy — Ramanujan formula for p(n) 94
Hardy, Godfrey Harold 94 196
Haselgrove, C.B. 186 196
Hecke operators 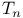 120 120
Hecke, Erich 114 120 133 196 197
Helly selection principle 179
Helly, Eduard 179
Hurwitz approximation theorem 145
Hurwitz zeta function 55 71
Hurwitz, Adolf 55 145
Invariants 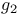 , , 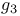 12 12
Inversion problem for Eisenstein series 42
Iseki, Sho 52 197
Iseki’s transformation formula 53
Jacobi theta function 91 141
Jacobi triple product identity 91
Jacobi, Carl Gustav Jacob 6 91 141
Klein modular invariant 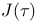 15 15
Klein, Felix 15
Kloosterman, H.D. 136
| Knopp, Marvin I. 197
Kronecker approximation theorem 148 150 154
Kronecker, Leopold 148
Lambert series 24
Lambert, Johann Heinrich 24
Landau, Edmund 186
Lehmer conjecture 22
Lehmer, Derrick Henry 22 93 95 197
Lehner, Joseph 22 91 111 197
LeVeque, William Judson 197
Linear space 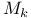 of entire forms 118 of entire forms 118
Linear subspace 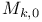 of cusp forms 119 of cusp forms 119
Liouville approximation theorem 146
Liouville function 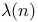 25 184 25 184
Liouville numbers 147
Liouville, Joseph 5 146 184
Littlewood, John Edensor 95
Mapping properties of 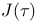 40 40
Mediant 98
Mellin inversion formula 54
Mellin, Robert Hjalmar 54
Mobius function 24 187
Mobius transformation 27
Mobius, Augustus Ferdinand 24 27 187
Modular forms 114
Modular forms and Dirichlet series 136
Modular function 34
Modular group  28 28
Modular group  , subgroups of 46 75 , subgroups of 46 75
Montgomery, H.L. 187
Mordell, Louis Joel 92 197
Multiplicative property of Hecke operators 126 127
Multiplicative property of Ramanujan tau function 93 114
Multiplicative property, of coefficients of entire forms 130
Neville, Eric Harold 110 197
Newman, Morris 91 111 197
Normalized eigenform 130
Order of an elliptic function 6
O’Brien, J.N. 91 196
Partition function p(n) 1 94
Period 1
Period parallelogram 2
Periodic zeta function 55
Petersson inner product 133
Petersson — Ramanujan conjecture 140
Petersson, Hans 22 133 140 197
Picard, Charles Emile 43
Picard’s Theorem 43
Product representation for 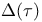 51 51
Quadratic forms 45
Rademacher path of integration 102
Rademacher series for p(n) 104
Rademacher, Hans 22 62 95 102 104 197
Ramanujan conjecture 136
Ramanujan tau function 20 22 92 113 131 198
Ramanujan, Srinivasa 20 92 94 136 191
Rankin, Robert A. 136 198
Reciprocity law for Dedekind sums 62
Representative of quadratic form 45
Riemann zeta function 20 140 155 185 189
Riemann, Georg Friedrich Bernhard 140 155 185 198
Rouche, Eugene 180
Rouche’s Theorem 180
Salie, Hans 136
Schoeneberg, Bruno 198
Sczech, R. 61 198
Selberg, Atle 136 198
Serre, Jean-Pierre 198
Siegel, Carl Ludwig 48 198
Simultaneous eigenforms 130
Spitzenform 114
Subgroups of the modular groups 46 75
Tau function 20 22 92 113 131
Theta function 91 141
Transcendental numbers 147
Transformation formula, of Dedekind 48 52
Transformation formula, of Dedekind, of Iseki 54
Transformation of order n 122
Turan, Paul 185 198
Turan’s Theorem 185 186
Univalent modular function 84
Uspensky, J.V. 94 198
Valence of a modular function 84
Values of 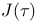 39 39
Values of Dirichlet series 170
van Wijngaarden, A. 22
Vertices of fundamental region 34
Watson, G.N. 109 198
Weierstrass 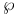 -function 10 -function 10
Weierstrass, Karl 6
Weight formula for zeros of an entire form 115
Weight of a modular form 114
Whiteman, Albert Leon 62 198
Zeros, of an elliptic function 5
Zeta function, Hurwitz 55
Zeta function, periodic 55
Zeta function, Riemann 140 155 185 189
Zuckerman, Herbert, S. 22
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 ,
,  ,
, 
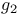 ,
, 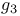
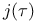 ,
, 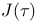
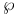 -function of Weierstrass
-function of Weierstrass 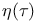
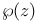
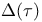
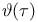

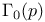

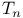
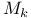 of entire forms
of entire forms 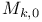 of cusp forms
of cusp forms