|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ash R. — Basic probability theory |
|
|
 |
| Предметный указатель |
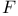 distribution see Distribution distribution see Distribution
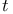 distribution see Distribution distribution see Distribution
Absolutely continuous random variable 53
Absolutely continuous random vector 72
Actions, set of 242
Admissible and inadmissible tests 247
Admissible risk points 248
Alternative, simple and composite 243
Average value see Expectation
Bayes estimate 260
Bayes estimate, with constant risk 262
Bayes estimate, with quadratic loss function 260
Bayes risk 244 260
Bayes test 244
Bayes’ Theorem 36 150
Bernoulli distribution see Distribution
Bernoulli trials 28 38 58 128 151 175 177 187 190 195 207 215
Bernoulli trials, generalized 29 (see also Distribution binomial)
Beta distribution see Distribution
beta function 133 261
Binomial distribution see Distribution
Boolean algebra 3ff
Borel measurable function 83
Borel sets 47 50
Borel — Cantelli lemma 205
Borel — Cantelli lemma, second 209
Bose — Einstein assumption 21
Cauchy distribution see Distribution
Central limit theorem 169ff 171
Characteristic function(s) 154ff
Characteristic function(s), correspondence, theorem for 156
Characteristic function(s), of a random vector 279
Characteristic function(s), properties of 166ff
Chebyshev’s inequality 126 127 129 206 208
coin tossing see Bernoulli trials; Distribution binomial
Combinatorial problems 15ff
Combinatorial problems, fallacies in 39ff
Combinatorial problems, multiple counting in 22
Complement of an event 4
Conditional density 136 148
Conditional distribution function 139 140 148
Conditional expectation 140ff
Conditional probability 33ff 130ff
Conditional probability function 98 142
Confidence coefficient 276
Confidence interval 276
Confidence set 278
Continuous random variable 69
Convergence, almost surely (almost everywhere) 204—206 208 210
Convergence, in distribution 170 171 175 176
Convergence, in probability 171 175 176 205 208 210
Convex function 262
Convexity of the risk set 248
Convolution theorem 164
Correlation 119ff
Correlation coefficient 120
Covariance 119
Covariance function 203
Covariance matrix 281
Cylinder 180
Cylinder, measurable 180
Decision function 242 243
Decision function, nonrandomized 242
Decision scheme 151
DeMorgan laws 7 9 11
Density function(s) 53
Density function(s), conditional 136 148
Density function(s), joint 70ff 181
Density function(s), marginal 78
Difference equation 24 39 182 186 195
Difference equation, characteristic equation of 183
Discrete probability space 15
Discrete random variables 51 95ff
Disjoint events 5
distribution 95
Distribution function(s) 52
Distribution function(s), conditional 139 140 148
Distribution function(s), joint 72
Distribution function(s), properties of 66ff
Distribution, 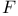 278 278
Distribution, 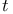 277 278 277 278
Distribution, Bernoulli 256 264 266 269 272
Distribution, Beta 260 268
Distribution, binomial 29 32 95 97—99 113 122 141 176 256 258 260 264 268
Distribution, Cauchy 161 166 264
Distribution, chi-square 165 275 276 278
Distribution, exponential 56 65 93 110 111 113 129 152 166 168 196 200— 202 256 263 264
Distribution, gamma 166 267 268
Distribution, geometric 195 196
Distribution, hypergeometric 33 256
Distribution, multidimensional Gaussian (joint Gaussian) 279ff
Distribution, negative binomial 196 264 268 272
Distribution, normal (Gaussian) 87 88 92 94 108 113 118 124—126 162 165 166 171 173—176 252 256 267 268 271 274—276 278
Distribution, Poisson 96—99 114 152 163 169 197 198 200 202 256 264 266 268 270 272
Distribution, uniform 54 73 76 84 92 93 113 118 141 149 150— 152 165 208 257 263 264 267 271 272
Dominated Convergence Theorem 231
Essentially constant random variable 85 115
Estimate 258
Estimate, Bayes 260
Estimate, Bayes, with constant risk 262
Estimate, inadmissible 272
Estimate, maximum likelihood 258
Estimate, minimax 262
Estimate, randomized 258 263
Estimate, risk function of 261
Estimate, unbiased 268
Estimate, uniformly minimum variance unbiased (UMVUE) 269
Estimation 152 242 243 258ff
Event(s) 2 11
Event(s), algebra of 3ff
Event(s), complement of 4
Event(s), contracting sequence of 67
Event(s), exhaustive 35
Event(s), expanding sequence of 66
Event(s), impossible 3 55
Event(s), independent 26 27
Event(s), intersection of 4
Event(s), mutually exclusive (disjoint) 5
Event(s), sure (certain) 3
Event(s), union of 4
Event(s), upper and lower limits of sequence of 204 209
Expectation 100ff
Expectation, conditional 140ff
Expectation, general definition of 103
Expectation, properties of 114ff
Exponential distribution see Distribution
Factorization theorem 266
Fatou’s Lemma 230
Fermi — Dirac assumption 20
Fourier series 167
Fourier transform 155
Gambler’s ruin problem 182ff 235
Gamma distribution see Distribution
Gamma function 109 133
Gaussian distribution see Distribution normal
Generating function 169 191ff
Generating function, moments obtained from 192
Geometric distribution see Distribution
Hypergeometric distribution see Distribution
Hypothesis 243ff
Hypothesis testing 151 242 243ff
Hypothesis testing, fundamental theorem of 246 (see also Test)
Hypothesis, a priori probability of 244
Hypothesis, composite 243
Hypothesis, null 243
Hypothesis, simple 243
Independence 25ff
Independence of sample mean and variance in normal sampling 274
Independent events 26 27
Independent random variables 80
| Indicators 122ff
Intersection of events 4
Jensen’s Inequality 262
Joint characteristic function 279
Joint density function 70ff 181
Joint distribution function 72
Joint probability function 76 96 180 181
Kolmogorov Extension Theorem 180
Laplace transform 155
Laplace transform, properties of 156 157
Lattice distribution 169
Law of Large Numbers, strong 129 203 206 207
Law of large numbers, weak 128 169 171 207
Lebesgue integral 114
Level of a test 246
Liapounov condition 175
Likelihood ratio 245
Likelihood ratio, test (LRT) 245
Limit inferior (lower limit) 204 209
Limit superior (upper limit) 204 209
Linearly dependent random variables 121 281
Loss function (cost function) 242
Loss function (cost function), quadratic 260
Marginal densities 78
Markov chain(s) 211ff
Markov chain(s), closed sets of 224
Markov chain(s), cyclically moving subclasses of 227
Markov chain(s), definition of 214
Markov chain(s), equivalence classes of states of 223
Markov chain(s), first entrance theorem for 220
Markov chain(s), initial distribution of 213
Markov chain(s), limiting probabilities of 2 30ff
Markov chain(s), state distribution of 214
Markov chain(s), state space of 213
Markov chain(s), states of 220ff
Markov chain(s), states of, aperiodic, periodic 229
Markov chain(s), states of, essential 229
Markov chain(s), states of, mean recurrence time of 230
Markov chain(s), states of, period of 226—229
Markov chain(s), states of, recurrent (persistent) 221ff
Markov chain(s), states of, recurrent null 233
Markov chain(s), states of, recurrent positive 233
Markov chain(s), states of, transient 221ff
Markov chain(s), stationary distribution for 236
Markov chain(s), steady state distribution for 215 237
Markov chain(s), stopping time for 217
Markov chain(s), strong Markov property of 219
Markov chain(s), transition matrix of 214
Markov chain(s), transition matrix of,  -step 214 -step 214
Markov chain(s), transition probabilities of 214
Maximum likelihood estimate 258
Maxwell — Boltzmann assumption 20
Mean see Expectation
Median 112
Minimax estimate 262
Minimax test 250
Moment-generating property of characteristic functions 167 168
Moments 107
Moments, central 108
Moments, joint 119
Moments, obtained from generating functions 192
Multinomial probability function 30 98
Mutually exclusive events 5
Negative binomial distribution see Distribution
Negative part of a random variable 104
Neyman — Pearson lemma 246
Normal distribution see Distribution
Observable 242
Order statistics 91
Partial fraction expansion 159
Poisson distribution see Distribution
Poisson random process 196ff
Poker 19 23 40
Positive part of a random variable 104
Power function of a test 253
Power of a test 246
Probability function 51
Probability function, conditional 98 142
Probability function, joint 76 96 180 181
Probability measure(s) 12
Probability measure(s), consistent 180
Probability measure(s), discrete 15
Probability space 12
Probability, classical definition of 1 13 16
Probability, conditional 33ff
Probability, frequency definition of 2 13
Probability, lOff Probability, a posteriori 36
Queueing 216
Random process 196
Random telegraph signal 203
Random variable(s) 46ff
Random variable(s), absolutely continuous 53
Random variable(s), central moments of 108
Random variable(s), characteristic function of 154ff
Random variable(s), classification of 51ff
Random variable(s), continuous 69
Random variable(s), definition of 48 50
Random variable(s), degenerate (essentially constant) 85 115
Random variable(s), density function of 53
Random variable(s), discrete 51 95ff
Random variable(s), functions of 58ff 84 85ff 94
Random variable(s), generating function of 192ff
Random variable(s), independent 80
Random variable(s), infinite sequences of 178ff
Random variable(s), linearly dependent 121 281
Random variable(s), moments of 107
Random variable(s), positive and negative parts of 104
Random variable(s), probability function of 51
Random variable(s), simple 101
Random vector 72
Random vector, absolutely continuous 72
Random walk 184ff
Random walk, combinatorial approach to 186ff
Random walk, simple 184
Random walk, simple, with absorbing barriers 184 185 215 228 240
Random walk, simple, with no barriers 185 186—191 193 195 215 228 240
Random walk, simple, with no barriers, average length of time required to return to 0 in 186 191 195
Random walk, simple, with no barriers, distribution of first return to 0 in 189
Random walk, simple, with no barriers, first passage times in 190
Random walk, simple, with no barriers, probability of eventual return to 0 in 185
Random walk, simple, with reflecting barriers 229 240
Rao — Blackwell theorem 263
Recurrent (persistent) states of a Markov chain 221
Reflection principle 188
Renewal Theorem 235
Risk function 261
Risk set 248
Sample mean 259 274
Sample space 2
Sample variance 259 274
Samples 16ff
Samples, ordered, with replacement 16
Samples, ordered, without replacement 16
Samples, unordered, with replacement 18
Samples, unordered, without replacement 17
Sampling from a normal population 274
Schwarz inequality 119 121 207
Sigma field 11
Simple random variable 101
Size of a test 246
Standard deviation 108
States of nature 241
Statistic, for a random variable 265
Statistic, for a random variable, complete 269
Statistic, for a random variable, sufficient 265
Statistical decision model 241
Statistics 241ff
Stirling’s formula 43 191
Stochastic matrix 212
Stochastic process 196
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



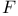 distribution
distribution 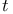 distribution
distribution  -step
-step