|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| McDuff D., Salamon D. — Introduction to Symplectic Topology |
|
|
 |
| Предметный указатель |
Curvature identity 222
Curvature of symplectic connection 221 222
Darboux chart 96 104
Darboux’s theorem 1 28 37 81 95
Darboux’s theorem equivariant 104
Darboux’s theorem for 2-manifolds 98
Darboux’s theorem for contact structures 112
Deformation equivalent fibrations 437
Deformation equivalent nonisotopic 6-manifolds 436
Deformation nonequivalent 6-manifolds 436
Dehn twist generalized 213—215 335
Dehn twist positive 455
Delzant 181 242
Diffeomorphism area-preserving see “Area-preserving diffeomorphism”
Diffeomorphism symplectic see “Symplectomorphism”
Diffeomorphism symplectic iff preserves capacity 377
Discrete Floer theory 370
Discrete Hamiltonian mechanics 288—293
Discrete holomorphic curve 370
Discrete loop space 408
Discrete method versus  -dim method 416 -dim method 416
Discrete path 291 292
Discrete symplectic action 291 345 346 396 406—408
Discrete symplectic action Morse theory 351
Discrete symplectic action number of fixed points 356
Discrete variational problem 277 286
Disjunction of Lagrangian submanifolds 423
Displacement energy and Hofer metric 382
Displacement energy and nonsqueezing 383
Displacement energy as relative capacity 384
Displacement energy of ball 385 386
Distribution contact 105
Distribution contact vector fields tangent to 110
Distribution horizontal 207 210
Distribution isotropic 100
Dolgachev surface 445
Donaldson 3 4 34 72 83 124 138 139 172 179 207 418 434 446 450 452
Duistermaat 159 191 192
Duistermaat — Heckman formula 191—196
Dynamics see “Hamiltonian dynamics”
Ehresmann 120
Ekeland 2 3 32 47 371 373 377 400 402
Ekeland — Hofer capacity 375
Eliashberg 2 32 108 116 252 262 339 366 377 383 419 422 426 430 432
Ellipsoid 31 58
Ellipsoid, capacity of 375
Ellipsoid, closed classification of 430
Ellipsoid, open classification of 428
Elliptic methods 3
Elliptic surface and fibre connected sum 253
Elliptic surface as blow-up 237
Embedding see “Symplectic embedding”
Embeddings of balls 246
Embeddings of balls construction 387
Energy 26
Energy, conservation of 22
Energy, displacement see “Displacement energy”
Energy, symplectic 2
Energy-capacity inequality 384—394
Enriques 134
Epstein 328
Equivariant cohomology 193
Equivariant cohomology localization theorem 194
Euclidean space 2
Euclidean space  325 325
Euclidean space  is contractible 325 is contractible 325
Euclidean space as Kaehler manifold 130
Euclidean space as symplectic manifold 82
Euclidean space as symplectic vector space 38 39
Euclidean space, billiards in 277
Euclidean space, exotic symplectic structure on 100 424
Euclidean space, generating functions on 280
Euclidean space, group actions on 165
Euclidean space, hamiltonian mechanics in 13—18
Euclidean space, hofer metric on 391
Euclidean space, mechanics in 12
Euclidean space, no exact Lagrangians 423
Euclidean space, reduces to  " 152 " 152
Euclidean space, symplectic geometry of 18—25
Euclidean space, symplectic invariants for subsets 3 375
Euclidean space, symplectic topology of 28—36
Euclidean space, twist maps in 269
Euclidean space, vector products on 118
Euler class 79
Euler — Lagrange equation 12 13 15 16 277 285 287
Evaluation map  to to 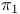 (M) 327 369 (M) 327 369
Evaluation map  to to  334 334
Exact symplectic action 162
Examples almost complex manifolds 118—120
Examples contact structure on 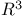 116 116
Examples cotangent bundle 90
Examples Duistermaat — Heckman formula 191
Examples exact Lagrangian immersion in 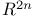 423 423
Examples existence problem 419
Examples exotic structure on 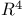 424 424
Examples first Chern class 79 80
Examples fixed points for maps of  342 342
Examples flux for annulus 332
Examples flux for torus 325
Examples generating function of type V 289
Examples Gromov width 432
Examples Hamiltonian flow on  22 22
Examples harmonic oscillator 26
Examples invariants for subsets of  428 428
Examples Kaehler manifolds 130 131 135
Examples large ball in  373 373
Examples nonKaehler symplectic manifold 89 251
Examples of blowing up 236—238
Examples of contact manifolds 106 108 109
Examples of convexity theorem 180—183
Examples of moment maps 165—170
Examples of nonequivalent symplectic structures 435
Examples of symplectic blowing up 242
Examples of symplectic manifolds 89 91—93
Examples ruled surface 248 249 442
Examples ruled surfaces 439
Examples Siegel upper half space 48
Examples symplectic fibrations 202
Examples toric manifolds 433
Examples, area form on 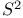 82 82
Examples, capacities 374
Examples, capacity of 2-manifold 400
Examples, exactness for  314 314
Exceptional divisor 234 239
Exceptional divisor as ball 239
Exceptional divisor Poincare dual of 235
Exceptional sphere 147 241 249
Exponential map 27
Fermat’s principle of least time 12
Fernandez 90
Feynman path integral 290
Fibration 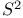 -bundles 156—159 202—206 -bundles 156—159 202—206
Fibration locally trivial 197
Fibration symplectic 197—202
Fibration symplectic coupling form 216
Fibration symplectic singular 213
Fibration, classification of 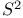 -bundles 203 -bundles 203
Fibration, compatible symplectic form on 198
Fibration, compatible symplectic form on deformation equivalence 439
Fibration, constructing symplectic 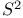 -bundles constructing symplectic form 199 -bundles constructing symplectic form 199
Fibration, elliptic 237
Fibration, Hamiltonian 226—232
Fibration, Hopf 153
Fibration, Lefschetz 455 456
Fibration, structure group of 198
Fibre critical points 306
Filling problem 115 419
Fintushel 446
First Chern class 37 71 73—80
First Chern class and connections 109 157
| First Chern class as obstruction 79
First Chern class axiomatic definition 74
First Chern class of K3 surface 254
First Chern class on Riemann surface 74
Fixed extrema of isotopy 392
Fixed point degenerate 340
Fixed point existence for twist maps 270
Fixed point geometrically distinct 270
Fixed point hyperbolic 348
Fixed point nondegenerate 340
Fixed point set as symplectic submanifold 186
Fixed point set normally hyperbolic 183
Fixed point theorems 34—36
Fixed point theorems of Lefschetz 343
Fixed point, number of 1
flexibility 2 33
Flexibility for open symplectic manifolds 257
Flexibility of contact structures 419
Floer 4 340 356 402 429 432
Floer homology 336 351 366—370
Floer theory 3 309
Floer theory discrete 370
Floer’s proof of Arnold’s conjectures 357
Floquet multipliers 266
Flux group 216 229 321
Flux group, discreteness of 323 324
Flux homomorphism 315—328
Flux homomorphism calculation for torus 325
Flux homomorphism exact case 320
Flux homomorphism geometric interpretation 317
Flux homomorphism has simple kernel 329
Flux homomorphism is surjective 318
Flux homomorphism is well defined 316
Flux homomorphism volume-preserving case 318
Fogerty 179
Foliation characteristic 29 87 99
Foliation with Reeb component 419
For linear map 289
Form global angular 109
Form primitive for  424 424
Fortune 369
Frankel 154 453
Franks 26 272
Fujiki 172
Fukaya 35 141 146 309 369 373
Gauge transformation 208
Gauge transformation, symplectic 219
Geiges 252 432
Gelfand — Robbin quotient 42 43
Generalized adjunction formula 453
Generating function 3 275—277
Generating function determined by H 283
Generating function for Lagrangians 303—310
Generating function for nbhd of 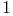 in Ham(M) 302 in Ham(M) 302
Generating function for symplectomorphism of torus 341
Generating function in billiard problem 278
Generating function of strong monotone map 275
Generating function of type S 280—283 292
Generating function of type V 289 297 406
Generating function on Ham(M) 293—303
Generating function quadratic at infinity 358 360
Generating function via discrete action 359—362
Geodesic 26 93
Geodesic broken 344
Geodesic flow 26
Geodesic for the Hofer metric 392
Geodesic local minimum of energy 27 286
Ginzburg 29 30 155 399
Givental 47 66 95 105 178 288 340 344 346 369
Global angular form 109
Goldman 179
Gole 277 288 339
Gompf 3 5 90 101 140 233 252—254 256 445
Gotay 90 201 211
Gottlieb 335
Gradient-like flow 355
Gradient-like flow number of fixed points 355
Graph of 1-form 99
Graph of isotopy 385 388
Graph of isotopy characteristics on 386
Graph of symplectomorphism 99 296
gray 90
Gray’s stability theorem 112
Greene 427
Griffiths 136 154 237 238 445 450
Gromov 2 4 31 33 65 81 100 147 233 237 251 252 257 262 312 325 358 377 401 417 419 423 424 426 430 452
Gromov invariants 434 437
Gromov invariants and Seiberg — Witten invariants 439—450
Gromov width 373 374 384
Gromov width upper bound for 432
Gromov — Witten invariants 232 436
Gromov’s compactness theory 144
Gromov’s flexibility theorem 257—261
Gromov’s nonsqueezing theorem see “Nonsqueezing theorem”
Group action condition to be Hamiltonian 162
Group action exact 162
Group action Hamiltonian 162
Group action of 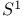 151 151
Group action of 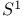 classification 433 classification 433
Group action of 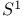 condition to be Hamiltonian 154 condition to be Hamiltonian 154
Group action semi-free 155 156
Group action weakly Hamiltonian 162
Group of contactomorphisms as Lie group 312
Group of diffeomorphisms algebraic structure 328
Group of diffeomorphisms as Lie group 312
Group of diffeomorphisms commutator subgroup is simple 328
Group of diffeomorphisms is perfect 328
Group of Hamiltonian symplectomorphisms see “Ham(M)”
Group of symplectomorphisms 20 33;
Group of volume-preserving diffeomorphisms 21 33
Group of volume-preserving diffeomorphisms algebraic structure 328
Group of volume-preserving diffeomorphisms as Lie group 312
Group, representations 5
Guillemin 5 151 159 162 179 180 185 197 207 210 215 226 242 250
Haar measure 46
Haefliger 262
Hall 265 275
Ham(M) 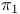 of 322 of 322
Ham(M) algebraic structure when M noncompact 329
Ham(M) as kernel of flux 318
Ham(M) closure of 323 324
Ham(M) for closed M, simplicity of 329
Ham(M) for noncompact manifolds 314 320
Ham(M) fragmentation lemma 329
Ham(M) juxtaposition of paths 313
Ham(M) nbhd of identity 302
Hamilton — Jacobi equation 280 283—286
Hamilton — Jacobi equation in contact geometry 111
Hamiltonian action 162
Hamiltonian action weak 162
Hamiltonian admissible 394
Hamiltonian circle action 151
Hamiltonian connection 226
Hamiltonian difference equations 290
Hamiltonian dynamics 24 25 165 265
Hamiltonian dynamics and Hamilton — Jacobi equation 284
Hamiltonian fibration 226
Hamiltonian flow 1 18 34 85
Hamiltonian flow, invariant tori for 284
Hamiltonian for symplectomorphism of cotangent bundle 92
Hamiltonian function 14 85
Hamiltonian function, extension of 402—405
Hamiltonian group action 161
Hamiltonian group action examples 166
Hamiltonian holonomy 215 226
Hamiltonian isotopy 88 294 295 313
Hamiltonian mechanics 12—27
Hamiltonian mechanics discrete 288
Hamiltonian quadratic growth 403
Hamiltonian symplectomorphism 88 294—303 313
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -dim method
-dim method 
 is contractible
is contractible  "
"  to
to 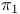 (M)
(M)  to
to 
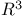





 in Ham(M)
in Ham(M)