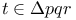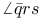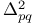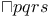|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Knuth D.E. — Axioms and Hulls |
|
|
 |
| Предметный указатель |
 69 72 73 92 69 72 73 92
3D convex hulls 72 89—92
3SAT problem 20
4L systems 43
4M systems 41
5M systems 93
Absolute value of signed points 12
Acyclic oriented matroids 35 40 55 93 96
Adjacent circuits 44
Adjacent points v 69
Adjacent points in vortex-free tournament 28
Adjacent pre-CC systems 19
Adjacent transpositions 29
Al-Aamily, E. 100
Algorithms, for convex hulls 47 48 52
Algorithms, for Delaunay triangulation 73
Algorithms, for sorting 29 62—65
Algorithms, incremental 47 48 52 73 98
Algorithms, parsimonious 2 62—67 98
Algorithms, verification of 49 78—79
Allowable sequences 94
Almost-canonical form 32
Alternating group 10
Anti-isomorphism 33
Antisymmetry 4 62
Approximation-based algorithms 67
Aragon, Cecilia Rodriguez 53 100
Arrangements of lines and pseudolines 34-35 94 96
Asano, Tetsuo 102
Asymmetry 64
Average-case analysis 50—51 65 80—81
Axiom 1 4 6 16 36
Axiom 2 4 6
Axiom 3 4 6
Axiom 4 4 7 10 29 36 42 45 56
Axiom 5 4 7—9 11 29 42 45 56
Axiom 5' 5 7 8 11
Axiom 6 42
Axiom C1-C5 71
Axiom C4' 90 95
Axiom L1-L3 43
Axiom M1-M4 40 93
Axiom R1'-R2' 64—65
Axiom R1-R2 62 64—65
Axiomatic methods, value of v—vi 1—3 62
Balanced trees 55
Bern, Marshall Wayne 96 97 100
Betweenness 25 30 94
binary search trees 47 55
Binary trees 62
Bjoerner, Anders 100
Bland, Robert Gary 95 98 100
Bokowski, Jurgen 95 96 100
Bose, Raj Chandra 103
Branch instructions in a data structure 48 74
Bubblesort 29—32
C 52 53 60
Cartesian products 68
Catalan, Eugene Charles, numbers 36
CC systems, defined 1 5 9
CCC systems, defined 2 70 93 97
CCCC systems 89 93 97 98
Change-ringing 29
Chazelle, Bernard Marie 96 100
Chirotopes 95
circuits 40
Clarkson, Kenneth Lee 81 100
clauses 20
Cocircuits 45
Cocircular points 82
Cocktail-shaker sort 29—32
Collinear points 4 6 55
Comparators 29
Comparison of algorithms 52
Comparison of keys 62—64
Complement, of a CC system 41
Complement, of a hypertournament 87
Complement, of a point 12
Complement, of a variable 20
Complementary satisfiability 20
complex numbers 70
Composition of CC systems 68
Computer Modern vii
Convex combinations 4 58
Convex hulls 1 2 45
Convex hulls in 3D 72 89—92
Convex hulls, algorithms for 47 48 52
Convex sets 93
coordinates 56 97
correctness 49 78—79
Cotransitivity 64
Counterclockwise predicate 1 3
Counterclockwise queries 16
Counterclockwise systems 5
Cramer, Gabriel, rule 4 90
Crossovers 34
CSAT problem 20
Cutpaths 38 68 97
Cycles 7 12
Cyclic symmetry 4 25—26
Dag triangulation algorithm 74 92 98
Daghull algorithm 47—51 52 55 67
DAGs 38 47 97
Data structure for triangulations 74 98
Degeneracy 55—61 82—86 94
Delaunay [Delone] triangulations 1 2 69
Delaunay [Delone] triangulations on the sphere 86
Delaunay [Delone] triangulations, algorithm for 73—77
Delaunay [Delone], Boris Nikolaevich 100
Determinant identities 4 5 70 90
Digraphs 7
Directed acyclic graphs 38
Directed graphs 7 19
Divide and conquer 62 97
Dowling, Thomas Allan 103
Dreiding, Andre 95 101
Dress, Andreas 100 101
Dual axioms 5 8 9
Dual hypertournaments 87
Dual matroids 45
Edelman, Paul Henry 35 101
Edelsbrunner, Herbert 96 101
Embedding 10 22 98
Empirical running times 54 81
Enumeration 13 35—40
Enumeration, numerical results 35 87
Eppstein, David Arthur 96 100
Equivalent reflection networks 31
Euclid 1
Extreme points 17 32 39 45 72 98
Fixed-point arithmetic 60 67 85
Fixing a point 43 70 87 93
Flipping a reflection network 34
Flipping edges in a triangulation 77
Floating-point arithmetic 1 56 60 67
Floating-point arithmetic, rigorous use of 86
Floyd, Robert W 29 101
Folkman, Jon 43 44 95 101
FORTRAN 60
Fortune, Steven Jonathon 62 101
Galvin, Frederick William 15 101
Garey, Michael Randolph 20 101
Gatroids 96
Generalized configurations of points 94
Geometric hypertournaments 88 92 95
Gonzales-Sprinberg, Gerard 97 101
Goodman, Jacob Eli 35 40 46 94 96 99 100 101 102
Graham, Ronald Lewis 102
Greene, Curtis 35 101
Gruenbaum, Branko 34 94 98 101 102
| Guibas, Leonidas Ioannis v vi 69 96 97 99 100 102
Gutierrez Novoa, Lino 94 102
Haegi, Hans 101
Halsey, Eric Richard 97 102
Horizon theorems 36 96
Hull insertion algorithm 52—55 66
Hulls see "Convex hulls"
Hyperoctahedral group 17
Hypertournaments 86—89 95
Ibaraki, Toshihide 102
IEEE standard floating-point 60 61 86
Imai, Hiroshi 102
In-vortex 12
Incircle predicate 1 2 69—71
Incremental algorithms 47 48 52 73 98
Independent axioms 6 71
Independent mutations 29 97
Instruction nodes 48 74
Interior transitivity 8 42
Interior triple systems 9—11
Interiority 4
Intersection of line segments 1
Inversions 24 29
Iverson, Kenneth Eugene, convention 14
Jaggi, Beat 102
Jaromczyk, Jerzy W. 102
Johnson, David Stifler 20 101
Jonassen, Arne 103
Klin, Mikhail H. 97 103
Knuth, Donald Ervin iii vii 2 3 53 68 97 102 103
Laffaille, Guy 97 100 101
Las Vergnas, Michel 95 96 98 100 103
Lascoux, Alain 35 103
latitude and longitude 86
Lawrence, James Franklin 95 101 103
Lee, Der-Tsai 96 100
Levi, Friedrich Wilhelm Daniel 34 94 96 103
Lexicographic order 57 58 68 97
Li, Zhenyu 103
Linear dependence 41
Linear ordering 10 26 30 56
MacMahon, Major Percy Alexander 14
Mandel, Arnaldo 96 103
Mani-Levitska, Peter 102
Maruani, J. 101
Mates 74
Matousek, Jiri 103
Matroid polytopes 97
Matroids 95
Matroids, oriented vii 35 40—45 92—93 95—97
Maurer, Hermann 101
MEMS 52
Merge sorting 62—63
Middle arcs 38
Milenkovic, Victor Joseph 103
Milnor, John Willard 40
Moon, John Wesley 15 103
Morris, Alun O. 100
Morris, Ernest 103
Muecke, Ernst Peter 101
Mutations 28—29
N-cubes 17 99
n-gons 11 18 30 32 39 43 46 50 53 79 81 87
n-ordered sets 94
Necklace patterns 14
Negating a point 12 17—19 87
Neighboring see "Adjacent"
Neighborly matroid polytopes 97
Nishizeki, Takao 102
Nondegeneracy 4
Nonisomorphic systems, enumeration of 13 97
North pole 35 38 72
NOT-ALL-EQUAL 3SAT 20
Notation, 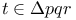 4 58 4 58
Notation, 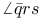 75 75
Notation, 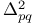 70 70
Notation, 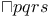 9 58 9 58
Notation, pqr 1 3
Notation, pqrs 1 69
Notation, |pqrs| 69 90
Notation, |pqr| 3
Nowacki, Werner 104
NP-complete 19
NP-hard 23
O'Rourke, Joseph 96 101
Odd-even transposition sort 29—31 36
Open problems 11 55 63 97—98
Oriented matroids, vii 35 40—45 92—93 95—97
Out-vortex 12
Pach, Janos 102
Pappus of Alexandria, theorem 6
Parallel sweep lines 24—27
Parentheses 36
Parsimonious algorithms vii 2 62—67 98
Patashnik, Oren 102
Paterson, Michael Stewart 102
Peel, Michael Harry 100
permutations 10 23 24
Perrin, R. 94 104
Perturbations 59—60 82—85
Plassman, Paul Eugene 96 100
Pollack, Richard 35 40 46 94 96 99 100 101 102
Polya, George 97
Postprocessing 55 67
Pre-CC systems 1 11 17 42
Preautomorphisms 18
Preisomorphisms 17 34 35 87 97
Premutations 28—29 97
Preprocessing 16
Preweak equivalence 34
Primitive sorting networks 2 29
Programmer on the street 66
Projective ordering 68
Projective plane 34
Pseudo-disks 98
Pseudo-hemispheres 96
Pseudolines 34—35 94 96
Quad-edge structure 72
Quicksort 51
Randomization 50 61 65 67
Rank 40 86 95
Realizable CC systems 6 29 35 40 60 66 96
Reducible tournaments 15
Reflection networks 29—35 68—69 94
Reorientation equivalence 97
Richter-Gebert [formerly Richter], Juergen 97 99 100 104
Ringel, Gerhard 96 104
Robust algorithms 2 67 85—86
Rockafellar, Ralph Tyrell 95 104
Rounding 60 67
Salesin, David Henry 99 102
SAT (satisfiability) problem 20
Schaefer, Thomas Jerome 20 104
Schuetzenberger, Marcel Paul 35 103
Scope of vertex in a CCC system 80
Scores in tournaments 51 65
Scores, vectors 15 46
Seidel, Raimund 53 96 99 100 101
Semispaces 94 98
Senatus Populusque Romanus 1
serial numbers 61 81 84
Serre, J. 101
Sharir, Micha 101 102
Shemer, Ido 98 104
Shor, Peter Williston 81 100
Signed bijections 17
Signed permutations 17
Signed points 12 16 40
Simple arrangements 34 96
Simplicial chirotopes 95
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте