|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Cofman J. Ч Numbers and shapes revisited: More problems for young mathematicians |
|
|
 |
| ѕредметный указатель |
 -bonacci sequence 4 -bonacci sequence 4
 -dimensional hypercubes 76Ч7 -dimensional hypercubes 76Ч7
 -dimensional hypercubes, problems 77Ч9 -dimensional hypercubes, problems 77Ч9
 -dimensional hypercubes, solutions 237Ч42 -dimensional hypercubes, solutions 237Ч42
 -dimensional Pascal pyramid 82Ч3 -dimensional Pascal pyramid 82Ч3
 -dimensional real euclidean spaces 71Ч6 -dimensional real euclidean spaces 71Ч6
 -dimensional Сmap-colouringТ problems 115 -dimensional Сmap-colouringТ problems 115
 -gons see Polygons -gons see Polygons
24-point sphere [of tetrahedron] 65 224
3-bonacci cuboids 12Ч13 141Ч2
3-bonacci hexagon 9 133Ч5
3-bonacci numbers 9 25Ч6 125
36 officers problem 103
Affine planes 108 109
Alternating groups 92
Appel, Kenneth 113
Archimedes of Syracuse 66
Associative operations 88 256 257
Barr, Mark 7
Bernoulli, Jakob 33
Besicovitch, A. S. 115
Binary operation 88
Binary relations [on the set] 46
BinetТs formula 6 17 19
BinetТs formula, generalization 252
BinetТs formula, proof 130
Binomial coefficients 81 243
Bos Ч Shrikhande Ч Parker theorem 104 Ч Shrikhande Ч Parker theorem 104
Cauchy Ч Bunyakowski inequality 54
Cauchy, Augustin Louis 52
CauchyТs inequality 51
CauchyТs inequality, generalization 53Ч5
CauchyТs inequality, problems 51Ч5
CauchyТs inequality, proofs 51Ч2 193Ч7
CauchyТs inequality, solutions 193Ч201
Cayley, Arthur 112
Centroid of tetrahedron 64 220
Centroid of triangle 64
Chinese remainder theorem 45 47Ч8
Chinese remainder theorem, applications 48Ч50
Chinese remainder theorem, problems 46Ч50
Chinese remainder theorem, solutions 187Ч92
Cissoid of Diodes 59 60 211
Coefficients, binomial 81 243
Coefficients, multinomial 81 243
Coefficients, trinomial 81 243 249
Colouring/painting problems 5Ч6 103 112Ч15
Colouring/painting problems, solutions 125Ч6 287Ч94
Combinatorics 103Ч20
Combinatorics, problems 105Ч12 114 118Ч21
Combinatorics, solutions 273Ч300
Congruences 46
Congruences, solution of 47 188 190
Connected graphs 115 116
Continuous functions 44
Coordinate hyperplanes 73
Crum, M. 115
Cubes, doubling of 58Ч9
Cubes, net of 239
Cubes, problems 62
Cubes, solutions 213Ч17
De MoivreТs Theorem 228
de Morgan, Augustus 112
Decimal expansions 34
Decimal fractions 32
Dehn, Max 66
DehnТs condition 66 67 227
Delian problem 58Ч9
DePalluel 107
Derangements 105 274
Dihedral angles [of polyhedra] 67
Diodes 59
Dodecahedra see Rhombic dodecahedra
Dots, patterns of 20Ч30
Dots, problems 23Ч30
Dots, solutions 151Ч64
Doubling of cube 58Ч9
Doubling of square 60Ч1
Equidecomposable shapes 66Ч9
Equilateral triangle, area 201Ч2
Equivalent relations 46
Euclid of Alexandria 56 71
Euclidean geometries 71
Euler, Leonhard 23 103 114
Eulerian circuits [of graphs] 116 118 295 296 297 298
EulerТs 36
EulerТs [figurate number] formula 23
EulerТs [figurate number] formula, proof 30 164
EulerТs [map-colouring] theorem 114 118
EulerТs [map-colouring] theorem, proof 119 290Ч1
Even permutation 92
Exclusion and inclusion, principle of 273
Facets [in hypercubes] 77
Farey series 35 172
Farey series, properties 173
Ferrer graphs 22 27Ч9 161Ч2
Ferrer graphs, advantage for studying partitions 27
fibonacci 3
Fibonacci gasket 17
Fibonacci numbers 3 25
Fibonacci numbers, generalized 4 6Ч8 81 84
Fibonacci numbers, LucasТ result 85 251
Fibonacci rectangles 6Ч7 8 131Ч2
Fibonacci sequence 3Ч4
Fibonacci sequence, problems 5Ч19
Fibonacci sequence, solutions 125Ч50
Fibonacci square 9
Fibonacci triangle 13Ч14 250
Fibonacci triangle, modulo-2 16 146
Fifteen puzzle 97Ч8
Fifteen puzzle, problem 98
Fifteen puzzle, solution 266Ч8
Figurate numbers 20 (see also Pentagonal numbers; square numbers; triangular numbers)
Figurate numbers, EulerТs formula 23 30 164
Finite affine plane 110
Finite group, operation table 107 277Ч8
Five-colour problem 114
Four-colour problem 112Ч13
Four-dimensional hypercubes, visualization 79Ч80
Fractals 4 17
Fractions 31
Full symmetric group 90
Functional equations, groups used in solution 93Ч5
GamblerТs ruin problem 86Ч7
GamblerТs ruin problem, solution 252Ч4
Gardner, Martin 7
Generalized Fibonacci numbers 4 6Ч8 81 84
Generators of groups 92
Geodesics 231
Geometries, euclidean geometries 71
Golden ratio 7
Golden rectangle 7 10
Golden rectangle, generalization 7Ч8
Golden rectangle, problem covering 10Ч11 137Ч9
Golden spiral 11
graphs 115Ч17
Graphs, definitions 115Ч16
Graphs, problems 118Ч20
Graphs, solutions 295Ч300
Great circles [of spheres] 70
Gregory, David 69
Group axioms 88
groups 88Ч102
Groups, alternating groups 92
Groups, and lattice points 96Ч7
Groups, basic properties 89Ч92
Groups, generators 92
Groups, meaning of term 88
Groups, permutation groups 90
Groups, problems 89Ч92 95Ч7 98Ч102
| Groups, solutions 255Ч72
Groups, use for solution of functional equations 93Ч5
Guthrie, Francis 112
H lderТs inequality 54 lderТs inequality 54
Haken, Wolfgang 113
Hamilton, William Rowan 120
Hamiltonian circuits [of graphs] 120 298Ч9
Heawood, P. J. 114
Higher-dimensional euclidean geometries 71
Higher-dimensional spaces 71Ч87
Higher-dimensional spaces, problems 73Ч80 82Ч7
Higher-dimensional spaces, solutions 235Ч54
Hilbert, David 66
HilbertТs third problem 66
Honeybee cells 61
Hoppe, R. 69
House-painting problems 5Ч6
House-painting problems, solutions 125Ч6
Hypercubes 76
Hypercubic lattice paths 80Ч7
Hyperplanes 73
Inclusion and exclusion, principle of 273
Inequalities 51
Inequalities, problems 51Ч7
Instant-insanity puzzle 120Ч1
Instant-insanity puzzle, problem 121
Instant-insanity puzzle, solution 299Ч300
Inversion, of permutation groups 91
Irrational numbers, KroneckerТs theorem 40Ч2
Isoperimetric theorem 51
Isoperimetric theorem, problems 56Ч7
Isoperimetric theorem, proofs 51
Isoperimetric theorem, solutions 201Ч7
Isoperimetric theorem, special cases 56Ч7
Isosceles triangle, area 202
K nig 62 nig 62
Kaplansky 106 276
Kepler, Johannes 61 62
Kronecker, Leopold 37
KroneckerТs theorem 40Ч2
KroneckerТs theorem, further applications 42Ч4
KroneckerТs theorem, problems 41Ч4
KroneckerТs theorem, proof 40Ч1
KroneckerТs theorem, solutions 182Ч6
Latin rectangles 115
Latin rectangles, normalized Latin rectangles 105
Latin squares 103Ч7
Latin squares, mutually orthogonal Latin squares 108 279
Latin squares, orthogonal Latin squares 104
Latin squares, problem 105Ч12
Latin squares, solutions 273Ч87
Lattice parallelograms 36 96
Lattice paths 80Ч7
Lattice paths, problems 82Ч5 86 87
Lattice paths, solutions 242Ч52
Lattice points 31 34Ч6
Lattice points, invisible 49Ч50
Lattice points, visible 35 48 172
Leonardo of Pisa 3 (see also Fibonacci)
Light rays linear congruences 47
Light rays, reflection 37 (see also Non-periodic light ray paths; reflected)
Logarithmic spiral 11
Lucas, 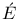 douard 85 106 251 douard 85 106 251
M nage numbers 106 nage numbers 106
M nage numbers, formula 106 nage numbers, formula 106
M nage numbers, formula, proof 276 nage numbers, formula, proof 276
Maclaurin, Colin 212
Mandelbrot, Benoit 17
Map, definitions 113
Map-colouring problems 103 112Ч15
Map-colouring problems, solutions 287Ч94
Married-couples problem 106
Married-couples problem, solution 274
Memory wheels 116Ч17
Memory wheels, problems 118Ч19
Memory wheels, solutions 294Ч8
Midspheres 230Ч1
Monge, point of 65
Multinomial coefficients 81 243
Mutually orthogonal Latin squares 108 279
Natural numbers, partitioning 22 26 28 29Ч30
Newton, Isaac 60 69
Nine-point circles 64 223
Non-periodic light ray paths 40Ч2
Normalized Latin rectangles 105
Odd permutation 92
Officers problem 103 104
Operation table of finite group 107 277Ч8
Operation table of set 255 256
Oriented circuits 116
Oriented graphs 116 295
Orthocentre of tetrahedron 64 65 220Ч2
Orthocentre of triangle 64
Orthogonal Latin squares 104
Orthogonality condition [for euclidean real planes] 75
Painting/colouring problems 5Ч6 103 112Ч15
Painting/colouring problems, solutions 125Ч6 287Ч94
Partitions of natural numbers 22 26 28 29Ч30
Pascal pyramid 82 244
PascalТs triangle 14 16
PascalТs triangle, modulo-2 16 145
PascalТs triangle, problems 14Ч17 42
PascalТs triangle, solutions 142Ч5
Pebble-heap problems 23Ч6
Pebble-heap problems, solutions 151Ч60
Pentagonal numbers 20
Pentagonal numbers, generalized 30
Periodic decimal numbers 31Ч3
Periodic fractions 32
Permutation groups 90
Permutation groups, inversion of 91
PickТs Theorem 36
Platonic solids 120 298
Platonic solids, problem 120
Platonic solids, solution 298Ч9 (see also Cubes; dodecahedra; tetrahedral)
Polygons, equidecomposability 66
Polygons, partition of 26
Polyhedra, dihedral angles 67
Polyhedra, equidecomposability 66Ч9
Principle of inclusion and exclusion 273
Projective planes 108 111
Pyramids, equidecomposability 66 68
Pyramids, volume calculation 66
Pythagorean numbers 20
R aumur, Ren aumur, Ren 62 62
Rado, R. 115
Rational numbers 31
Reading list 301Ч3
Recurrence relations for Fibonacci numbers 3 4 125 127 148
Recurrence relations, how to solve 17Ч19
References listed 301Ч3
Reflected light rays 37
Reflected light rays, problems 37Ч40
Reflected light rays, solutions 175Ч81
Repunits 31Ч3 167
Residue class 46
Rhombic dodecahedra 61Ч2 120 298
RubikТs cube 98Ч101
RubikТs cube, problems 101Ч2
RubikТs cube, solutions 268Ч72
Seating-arrangement problem 106
Seating-arrangement problem, solutions 274 277
Set, binary operation on 88
Set, operation table for 255 256
Sierpi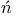 ski gasket 16 17 ski gasket 16 17
Sierpi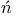 ski, Waclaw 17 ski, Waclaw 17
Silver hexagon, problem covering 11Ч12 139Ч41
Silver polygons 8
Sphere-packing problems 69
Spheres, problems 69Ч70
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



 -bonacci sequence
-bonacci sequence  -dimensional hypercubes
-dimensional hypercubes  Ч Shrikhande Ч Parker theorem
Ч Shrikhande Ч Parker theorem  lderТs inequality
lderТs inequality 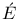 douard
douard  ski gasket
ski gasket