Авторизация
Поиск по указателям
Lions J-L., Dautray R. — Mathematical Analysis and Numerical Methods for Science and Technology: Volume 2: Functional and Variational Methods
Обсудите книгу на научном форуме Нашли опечатку?
Название: Mathematical Analysis and Numerical Methods for Science and Technology: Volume 2: Functional and Variational MethodsАвторы: Lions J-L., Dautray R. Аннотация: These 6 volumes - the result of a 10 year collaboration between the authors, two of France's leading scientists and both distinguished international figures - compile the mathematical knowledge required by researchers in mechanics, physics, engineering, chemistry and other branches of application of mathematics for the theoretical and numerical resolution of physical models on computers. Since the publication in 1924 of the "Methoden der mathematischen Physik" by Courant and Hilbert, there has been no other comprehensive and up-to-date publication presenting the mathematical tools needed in applications of mathematics in directly implementable form. The advent of large computers has in the meantime revolutionised methods of computation and made this gap in the literature intolerable: the objective of the present work is to fill just this gap. Many phenomena in physical mathematics may be modeled by a system of partial differential equations in distributed systems: a model here means a set of equations, which together with given boundary data and, if the phenomenon is evolving in time, initial data, defines the system. The advent of high-speed computers has made it possible for the first time to calculate values from models accurately and rapidly. Researchers and engineers thus have a crucial means of using numerical results to modify and adapt arguments and experiments along the way. Every facet of technical and industrial activity has been affected by these developments. Modeling by distributed systems now also supports work in many areas of physics (plasmas, new materials, astrophysics, geophysics), chemistry and mechanics and is finding increasing use in the life sciences.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2000Количество страниц: 608Добавлена в каталог: 12.02.2014Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Operator in Banach or Hilbert spaces, Hermitian, positive definite 353 Operator in Banach or Hilbert spaces, Hilbert — Schmidt 357 Operator in Banach or Hilbert spaces, isometric 355 Operator in Banach or Hilbert spaces, nilpotent 319n Operator in Banach or Hilbert spaces, nuclear 331 Operator in Banach or Hilbert spaces, orthogonal projection 354 Operator in Banach or Hilbert spaces, partially isometric 356 Operator in Banach or Hilbert spaces, projection 325 355 Operator in Banach or Hilbert spaces, quasi-nilpotent 319 Operator in Banach or Hilbert spaces, restriction 307 Operator in Banach or Hilbert spaces, symmetric 361 Operator in Banach or Hilbert spaces, transpose 322 343 Operator in Banach or Hilbert spaces, unitary 355 Operators (not necessarily bounded) with closed image 346 Operators (not necessarily bounded), accretive 372 Operators (not necessarily bounded), bounded 274 Operators (not necessarily bounded), closable 335 Operators (not necessarily bounded), closed 335 361 Operators (not necessarily bounded), compact 123 Operators (not necessarily bounded), continuous 274 Operators (not necessarily bounded), essentially self-adjoint 336 Operators (not necessarily bounded), invertibility 319 Operators (not necessarily bounded), lifting 110 Operators (not necessarily bounded), maximal symmetric 336 Operators (not necessarily bounded), mutually transposed 309 Operators (not necessarily bounded), normal 366 Operators (not necessarily bounded), sectorial 373 Operators (not necessarily bounded), self-adjoint 362 Operators (not necessarily bounded), transpose 309 343 Operators, linear differential of constant force 245 Operators, linear differential with analytic coefficients 163 Operators, linear differential with constant coefficients 170 Operators, linear differential, 175 Operators, linear differential, antisymmetric 155 Operators, linear differential, characteristic polynomial of 171 Operators, linear differential, decomposable 190 Operators, linear differential, elliptic 176 Operators, linear differential, formal series associated with 150 Operators, linear differential, hyperbolic 190 Operators, linear differential, hypo-analytic 176 235 Operators, linear differential, hypo-elliptic 177 221 Operators, linear differential, locally finite 149 Operators, linear differential, order of 154 Operators, linear differential, parabolic 202 Operators, linear differential, partial order of 157 Operators, linear differential, principal part of 154 Operators, linear differential, semi-elliptic 247 Operators, linear differential, strictly hyperbolic 196 Operators, linear differential, strongly elliptic 175n 224 Operators, linear differential, symmetric 155 Operators, linear differential, transpose 453 Operators, linear differential, ultra-hyperbolic 201 Operators, linear differential, weakly parabolic 222 Order of a linear differential operator 154 Orthogonal decomposition 119 Orthogonal elements 294 Orthogonal projection of an operator 298 355 Orthogonal projector 298 355 Orthonormal base 300 Orthonormal family 299 Paley — Wiener theorem 505 Paley — Wiener — Schwartz theorem 510 Parabolic boundary 252 Parabolic comparison principle 257 Parabolic maximum principle 252 Parabolic operator 202 Parallelogram identity 293 Parseval's relation 53 301 357 503 Partial Fourier transform 513 Periodic distribution 7 Periodic transform 9n Plancherel's formula 503 Poincare's constant 127 Poincare's inequality 126 379 Poisson's integral formula 18 Poisson's summation formula 512 Positive definite form 357 Pre-Hilbert space 293 Primitives of a distribution 477 Primitives of the Dirac measure 482 Principal part of a linear differential operator 154 Principle of the strong maximum 251 Principle of the strong parabolic maximum 265 Principle of the weak maximum 259 Principle of uniform boundedness 275 Projection 296 325 Projection operator 355 Projector 355 Propagation of singularities 210 Proper mapping 481 Properly elliptic operator 437 Pseudo functions Pf 471 Quadrature formula 61 Quasi-nilpotent operator 319 Quotient operator 308 Quotient space 308 Radial function 56 Rank of an operator 330 Reduced minimal modulus 342 Reflexivity 286 302 Regularisation 81 104 461 Regularity of solutions of variational problems, global 426 437 Regularity of solutions of variational problems, interior 426 Relatively compact part 327n Rellich's theorem 123 Resolvent operator 320 Resolvent set 320 Restriction of a distribution 474 Restriction of an operator 307 Riemann — Lebesgue theorem 500n Riesz representation theorem 302 Riesz — Frechet theorem 302n Robin's problem 400 448 Salient cone 189 Saltus 470 Scalar product 291 Scalar product on a Hilbert space 293 Scalar product, Hermitian 291 Schauder spaces 3 Schauder's theorem 329 Scheme with five points 88 Scheme with three points 84 Schmidt's orthonormalisation method 300 Schrodinger operator 180 192 Schwartz's proposition 526 Schwartz's theorem of kernels 528 Sectorial operators 373 Self-adjoint operator 351n Semi-ball 271 Semi-groups 225 Semi-norm 270 Sesquilinear form 292 351 367 Sesquilinear form, adjoint 353 Sesquilinear form, non-degenerate 292 Sesquilinear form, non-negative 293 Sesquilinear form, positive definite 292 Sesquilinear form, uniformly strongly elliptic 389 Sobolev spaces 92 138 Sobolev spaces with weights 141 Sobolev spaces, density theorems 102 Sobolev spaces, trace theorems 113 140 Sobolev's embedding theorem 100 Sobolev's inclusion 131 Sobolev's injections 139 Space of bounded operators 310 Space of distributions 463 Space of tempered distributions 507 Space of test functions 457 Space of traces 22 Space, Banach 272 Space, complete metric 272 Space, energy 269 Space, Frechet 272 Space, Hilbert 291 Space, locally convex topological 271 Space, metric 272 Space, metrisable 272n Space, normed vector 272 Space, pre-Hilbert 291 Space, reflexive normed 286 Space, Schauder 3 Space, separable 283 300 Space, separated topological 271 Space, Sobolev 92 Spectral radius 319 Spectrum of an operator 84 320 Speed of propagation 215 Statical problems of elasticity 411 Stirling's formula 234n Strong convergence 287 Strong maximum principle 263 Strong parabolic maximum 265 Sub-critical medium 405 Subharmonic function 251 Sum of operators 307 Summability 15 Support cone of an elementary solution 189 Support of a distribution 474 Surjection 539 Surjective map 539 Table of Fourier transforms of distributions 532 Table of Hankel transforms 57 Table of Mellin transforms 40 Tchebycheff polynomials 81 Tempered distributions 184 507 Tensor product of two distributions 480 Tensor product of two functions 480 Test functions 457 Topological supplement 326 Topological vector space 270 Total family 300 Totally bounded set 328n Trace map 108 Traces of Sobolev spaces 113 Transform, bilateral Laplace 25 Transform, discrete Fourier 59 Transform, fast Fourier 64 Transform, Fourier 2 Transform, Hankel 2 40 Transform, Laplace 2 Transform, Mellin 2 24 Transformation to the left 306 Transformation to the right 306 Transformation, Cooley — Tukey 64 Transformation, Good — Winograd 66 Transmission conditions 401 Transmission problem 400 Transpose of a linear differential operator 153 Transpose of an operator in Banach or Hilbert space 343 Truncation 103 461 Uniform boundedness 275 Uniform derivative 332 Unitary operator 355 Variation of a function 478n Variation of parameters 479 Vector space 270 Virtual power 412 von Neumann's theorems 362 Wave front set 211n Wave operator 180 Weak compactness 289 Weak convergence 287 Weak derivative 332 Weak differentiability 304 Weak holomorphy 305 333 Weak maximum principle 259 Weak topology 304 Weak-star convergence 290 Weakly parabolic operator 221 Weight function 242 Weighted Sobolev space 141 Well-posed Cauchy problem 214 217 Young's inequality 459
Реклама
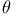-strongly elliptic 
|
|
О проекте