Авторизация
Поиск по указателям
De Barra G — Measure theory and integration
Обсудите книгу на научном форуме Нашли опечатку?
Название: Measure theory and integrationАвтор: De Barra G Аннотация: This updated and introductory text approaches integration via measure as opposed to measure via integration, an approach which makes it easier to grasp the subject. Apart from its central importance to pure mathematics, the material is also relevant to applied mathematics and probability, with proof of the mathematics set out clearly and in considerable detail. Numerous worked examples necessary for teaching and learning at undergraduate level constitute a strong feature of the book, and after studying statements of results of the theorems, students should be able to attempt the 300 problem exercises which test comprehension, for which detailed solutions are provided. The book stems from a long-running successful course and presents the knowledge and experience of Dr. de Barra who has long taught and researched measure theory in London University. This 2nd edition has been updated by the attachment of Afternotes indicating how the subject has developed from material in the text, and misprints from the original have now been corrected. The only pre-requisite is a first course in analysis, and what little topology required is developed within the text.
Язык: Рубрика: Математика /
Статус предметного указателя: Готов указатель с номерами страниц
ed2k: ed2k stats Год издания: 2000
Количество страниц: 236
Добавлена в каталог: 11.02.2014
Операции: Положить на полку |
Скопировать ссылку для форума |
Скопировать ID
Предметный указатель
18 32 36 205 18 32 36 205 109 110 109 110 94 98 139 149 171 179 181 93 Absolute convergence 21 64 Absolutely continuous functions 160 163 228 Absolutely continuous functions, measure 139 161 Algebra 30 Algebra, 30 Almost everywhere (a.e.) 40 104 Almost uniform convergence 125 128 132 Almost uniformly fundamental 127 Angular measure 187 Approximating measure 45 Arithmetic-geometric mean inequality 114 Axiom of Choice 17 42 Borel measurable 40 165 169 187 211 233 Borel measure 102 158 Borel set 32 43 98 101 102 187 203 211 228 Bounded linear functional 148 174 175 BV [a, b] 81 160 163 Cantor set 24 37 157 202 227 Cantor's function 43 45 196 203 Cantor-like sets 23 26 50 200 202 203 cardinal number 22 203 Cartesian product 15 176 Cauchy sequence 20 118 122 Change of variable 167 234 Characteristic function 22 39 Closure 17 Complement 15 Complete measure 94 101 142 Complete metric space 20 118 124 Completion of a measure 100 102 185 Complex-valued functions 189 Convergence in measure 121 128 131 221 Convergence in the mean 123 128 131 132 221 229 Convergence in the mean of order p 123 128 131 132 223 Convergence, absolute 21 64 Convergence, almost everywhere 118 125 128 Convergence, almost uniform 125 128 132 Convergence, uniform 125 128 131 132 229 235 Convergence, uniform a.e. 125 128 Convex function 5 111 163 215 Convolution 191 Countable set 22 Countable subadditivity 29 95 Countably additive 31 95 De Morgan's laws 15 Dense 17 Density of a set 35 Derivates 77 209 Differentiable 65 87 111 Distance (between sets) 43 Distribution function 156 158 Domain 21 Dual space 148 151 152 227 Egorov's theorem 126 222 Elementary set 176 Equipotent 22 Equivalence class 17 Equivalence class, relation 16 Essential infimum (ess inf) 41 104 Essential supremum (ess sup) 40 104 Essentially bounded 41 104 Euclidean space 16 Extended real numbers 37 Extension of a function 21 Extension of a measure 95 Fatou's lemma 57 58 60 63 88 105 119 123 204 205 208 213 Fourier transform 192 Fubini's theorem 182 Function of bounded variation 81 160 163 Function, Borel 40 165 169 205 228 233 Function, Cantor's 43 45 196 203 Function, characteristic 22 Function, composite 21 Function, convex 5 111 163 215 Function, distribution 156 Function, integrable 61 106 164 Function, Lebesgue's 25 26 78 157 159 163 196 211 234 Function, measurable 38 93 103 169 Function, non-differentiable 79 Function, simple 54 Function, step 22 Function, strictly concave 52 Function, subadditive 30 201 Fundamental in measure 122 Fundamental sequences 121 Generated algebra 32 Generated algebra, 32 Generated algebra, 94 Generated algebra, ring 94 Hahn decomposition 133 136 137 138 141 223 224 225 Hausdorff measure 45 52 99 158 203 Hausdorff measure, dimension 50 53 159 203 Hausdorff measure, measure function 45 158 Hausdorff measure, outer measure 45 Heine — Borel theorem 18 Helly's theorem 158 Hereditary 94 Hoelders inequality 115 148 150 151 216 217 223 235 Identity mapping 21 Indefinite integral 87 169 171 Induction 16 Infimum 18 Integrable 61 106 164 integral 54 105 106 Integration by parts 65 163 164 Intervals 27 Inversion theorem 195 Iterated limit 20 Iterated limit, integral 182 231 232 233 Jensen's inequality 113 195 Jordan decomposition 137 139 225 Laplace transform 191 Lebesgue decomposition 146 147 Lebesgue dominated convergence theorem 63 107 123 Lebesgue function 25 26 78 157 159 163 196 211 234 Lebesgue integral 54 55 Lebesgue measurable functions 38 Lebesgue measurable set 30 185 Lebesgue measure 31 94 185 Lebesgue monotone convergence theorem 57 105 Lebesgue outer measure 27 Lebesgue set 90 91 Lebesgue — Stieltjes measure 156 Lebesgues Differentiation Theorem 84 85 Limit, lower 18 Limit, one-sided 19 Limit, point 18 Limit, upper 18 Lindeloef's theorem in 23 84 Lindeloef's theorem in 23 Linear functional 148 172 Lipshitz condition 163 228 Mean fundamental sequence 147 Measurable 30 93 97 Measurable function 38 93 103 169 Measurable rectangle 176 Measurable space 102 Measure 31 47 94 153 156 157 179 Measure space 102 Metric 17 116 118 124 125 221 Metric outer measure 49 Minkowski's inequality 115 118 218 219 226 Modulus of continuity 52 159 Monotone class 177 180 Mutually singular measures 137 Negative part of a function 61 Negative set 134 Negative variation of a function 81 164 Non-differentiable function 79 Non-measurable set 42 179 203 Norm 109 110 148 172 226 227 Normed vector space 147 Null set 134 O, o notation 20 One-to-one mapping 21 open 17 Ordinals 182 Ordinate set 184 Outer measure 27 45 94 Parseval's theorem 193 196 Partitions 71 Plancherel transform 194 Positive linear functional 172 Positive part of a function 61 Positive set 134 Positive variation of a function 81 164 primitive 156 157 159 Principle of Finite Induction 16 Product measure 181 Product of measurable spaces 177 Product space 176 185 Pseudometric 17 95 211 Radon — Nikodym derivative 143 167 Radon — Nikodym theorem 139 RANGE 21 rectangle 176 Rectifiable 82 Reflexive space 227 Regular measure 35 Relative topology 18 Riemann integrable 71 Riemann integral 55 71 208 Riemann — Lebesgue lemma 75 235 Riesz Representation Theorem for 151 Riesz Representation Theorem for 148 Riesz Representation Theorem for C (I) 172 Ring 93 Schwarz inequality 15 216 218 Sections of functions 179 Sections of sets 178 Sequence, Cauchy 20 Sequence, closed 17 Sequence, compact (closed and bounded) 18 51 159 Sequence, dense 17 Sequence, double 20 Sequence, Lebesgue 90 91 Sequence, measurable 30 93 97 Sequence, monotone decreasing 20 Sequence, monotone increasing 19 Sequence, non-measurable 42 179 203 Sequence, nowhere dense 17 201 Sequence, open 17 Sequence, perfect 17 25 Series, absolutely convergent 21 64 Set, Borel 32 43 98 101 102 187 203 211 228 Sgn x 22 Signed measure 133 Simple function 54 Strictly convex 111 Subadditive 29 95 Support of a measure 157 Supremum 18 Symmetric difference 15 Tchebychev's inequality 107 topology 17 Total variation of a function 81 Total variation of a measure 138 Translation invariance 28 46 186 Uniform convergence 125 128 131 132 229 235 Uniformly fundamental 221 union 15 Unit sphere 187 Variation (of a function), bounded 81 Variation (of a function), negative 81 Variation (of a function), positive 81 Variation (of a function), total 81 Variation (of a measure), total 138 Weakly convergent 120
Реклама
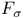-sequence 
-sequence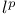 
-norm 
-space 
-finite 
|
|
О проекте