Авторизация
Поиск по указателям
Howie J.M. — Fields and Galois Theory
Обсудите книгу на научном форуме Нашли опечатку?
Название: Fields and Galois TheoryАвтор: Howie J.M. Аннотация: Fields are sets in which all four of the rational operations, memorably described by the mathematician Lewis Carroll as "perdition, distraction, uglification and derision", can be carried out. They are assuredly the most natural of algebraic objects, since most of mathematics takes place in one field or another, usually the rational field Q, or the real field M, or the complex field С This book sets out to exhibit the ways in which a systematic study of fields, while interesting in its own right, also throws light on several aspects of classical mathematics, notably on ancient geometrical problems such as "squaring the circle", and on the solution of polynomial equations.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2005Количество страниц: 225Добавлена в каталог: 09.02.2014Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
94 159 Abel, Niels Henrik (1802-1829) 3 Abelian basis theorem 151 Abelian group 3 149 Abel’s theorem 145 Addition (of polynomials) 34 Algebraic element 59 Algebraic extension 59 Algebraic independence 175 Algebraic number 59 Alternating group 162 Associates 3 Associative law 1 Automorphism 9 Automorphism, Frobenius 90 Automorphism, identity 94 Basis Theorem 151 Canonical extension (of an isomorphism) 37 Cantor, Georg Ferdinand Ludwig Philipp (1845-1918) 61 Cardano, Girolamo (1501-1576) 127 Centraliser 157 Centre (of a group) 157 Characteristic 17 Characteristic polynomial 64 Class equation 156 Commutative law 1 3 Commutative ring 2 Conjugate elements 156 Constructible point 75 183 Constructible polygon 189 Coprime 26 28 Coset 21 Coset, left 21 Coset, right 22 Cubic equation 128 CYCLE 160 Cyclic extension 140 Cyclic group 21 Cyclotomic polynomial 133 135 Dedekind, Julius Wilhelm Richard (1831-1916) 92 Degree of a polynomial 34 Degree of an extension 52 Degree, transcendence 176 Descartes, Ren 127 Dimension (of a vector space) 52 Direct product 153 Direct sum 149 Disjoint cycles 160 Division 4 Division algorithm 25 Divisor 4 Divisor, proper 4 Domain 2 Domain, Euclidean 25 33 38 Domain, factorial 30 Domain, integral 2 Domain, principal ideal 26 Domain, unique factorisation 30 Duplicating the cube 74 77 Eisenstein, Ferdinand Gotthold Max (1823-1952) 46 Eisenstein’s Criterion 46 Embedding 9 Equation, cubic 128 Equation, quadratic 127 Equation, quartic 130 Equation, quintic 173 Equivalence relation 5 Euclid of Alexandria (c. 325-265 B.C.) 25 187 Euclidean algorithm 27 39 Euclidean Domain 25 33 38 Extension 18 51 Extension by radicals 132 Extension, algebraic 59 Extension, cyclic 140 Extension, finite 52 Extension, finitely generated 175 Extension, Galois 115 Extension, infinite 52 Extension, normal 103 Extension, separable 110 Extension, simple 55 Extension, transcendental 59 175 Factor 4 Factor group 22 Factor, proper 4 Factorial domain 30 39 Fermat prime 191 Fermat, Pierre de (1601-1665) 191 Ferrari, Lodovico (1522-1565) 127 Ferro, Scipione del (1465-1526) 127 Field 2 Field, finite 85 Field, Galois 87 Field, of algebraic numbers 60 Field, of fractions 15 Field, perfect 110 Field, splitting 79 86 Finite extension 52 Finite field 85 Formal derivative 85 Frobenius automorphism 90 Frobenius, Ferdinand Georg (1849-1917) 90 Fundamental theorem of algebra 42 Galois correspondence 99 Galois extension 115 Galois field 87 Galois group 94 Galois, Evariste (1811-1832) 1 Gauss, Johann Carl Friedrich (1777-1855) 29 44 187 Gaussian integers 29 33 Gauss’s Lemma 44 General polynomial 178 Greatest common divisor 26 39 Group 3 Group, abelian 3 149 Group, alternating 162 Group, cyclic 21 Group, finite 21 Group, Galois 94 Group, of automorphisms 94 Group, of prime power order 157 Group, of units 3 Group, realisable 180 Group, simple 164 Group, soluble 154 163 167 Group, symmetric 160 Hermite, Charles (1822-1901) 61 180 Highest common factor 26 Hilbert, David (1862-1943) 140 Homomorphic image 22 Homomorphism 8 Homomorphism, natural 10 22 Homomorphism, substitution 40 Ideal 6 Ideal, principal 7 Identity 2 Identity automorphism 94 Indeterminate 35 INDEX 157 Infinite extension 52 Integral domain 2 Irreducible 29 39 Isomorphic 9 Isomorphism 9 22 Kernel 9 22 100 Klein, Felix Christian (1854-1912) 180 Lagrange, Joseph-Louis (1736-1813) 21 122 Lagrange’s Theorem 21 Leading coefficient 34 Lindemann, Carl Louis Ferdinand von (1852-1939) 61 78 Linearly independent 92 Liouville, Joseph (1809-1882) 61 Minimum polynomial 57 Monic polynomial 34 Monomorphism 9 92 Multiplication (of polynomials) 34 Natural homomorphism 10 22 Norm 140 Normal closure 106 Normal extension 103 Normal subgroup 22 Nullity 100 Partition 21 Perfect field 110 Permutation 162 Permutation, even 162 Permutation, odd 162 Perpendicular bisector 71 Poincar 180 Polynomial 33 Polynomial ring 35 Polynomial, characteristic 64 Polynomial, constant 34 Polynomial, cubic 34 128 Polynomial, cyclotomic 133 135 Polynomial, elementary symmetric 177 Polynomial, general 178 Polynomial, linear 34 Polynomial, minimum 57 Polynomial, monic 34 Polynomial, quadratic 34 127 Polynomial, quartic 34 130 Polynomial, quintic 34 173 Polynomial, separable 110 Polynomial, sextic 34 Polynomial, symmetric 177 Prime subfield 18 86 Principal ideal 7 Principal ideal domain 26 39 Quartic equation 130 Quintic equation 173 Quotient 25 Quotient group 22 Radical extension 132 Rank 100 Rational forms 36 Realisable group 180 Reflexive property 5 Regular polygon 187 Relatively prime 26 Remainder 25 Remainder theorem 40 Residue class 10 Residue class ring 10 Ring 1 Ring, commutative 2 Ring, with unity 2 Root (of a polynomial) 40 Ruler and compasses 71 75 Separable extension 110 Separable polynomial 110 Shafarevich, Igor Rostislavovich (1923-) 180 Simple extension 55 Simple group 164 Soluble by radicals 132 169 170 172 Soluble group 154 163 167 169 170 172 Solution by radicals 131 Splitting field 79 86 Splitting field, uniqueness 81 Squaring the circle 74 78 Subfield 6 Subfield, prime 18 Subgroup 21 Subgroup, normal 22 Subgroup, Sylow 156 Subring 6 Substitution homomorphism 40 Sylow subgroup 156 Symmetric group 160 Symmetric polynomial 177 Symmetric property 5 Tartaglia, Nicolo (1499-1557) 127 Trace 140 Transcendence degree 176 Transcendental element 175 Transcendental extension 59 Transcendental number 59 Transitive property 5 Transposition 161 Trisecting the angle 74 77 Unique factorisation domain 30 39 UNIT 3 Unity element 2 Vector space 51 Zero (of a polynomial) 40
Реклама
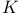-automorphism 
-group 
(1596-1650)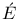 
, Jules Henri (1854-1912) 
|
|
О проекте