Авторизация
Поиск по указателям
Rosenhouse J. — The Monty Hall Problem: The Remarkable Story of Math's Most Contentious Brain Teaser
Обсудите книгу на научном форуме Нашли опечатку?
Название: The Monty Hall Problem: The Remarkable Story of Math's Most Contentious Brain TeaserАвтор: Rosenhouse J. Аннотация: "Let's Make a Deal," with its popular host Monty Hall, was a staple of 1970s game shows, with squirming contestants trying to guess which of three doors concealed the grand prize. The contestant chooses a door, but does not open it. Monty opens a different door, always empty. The contestant faces a choice: stick with his original door or switch to the remaining door?
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2009Количество страниц: 207Добавлена в каталог: 08.02.2014Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Never-never land 139 New Year’s 6 New York 8 Newman, Paul 2 Newtonian mechanics 84 Nickerson, Raymond 147-48 Non-arbitrariness 170 172 Nucleus 127 Numerator 43 Objective probability 86 Ordered pairs 4 45 58 Ordered triples 47 61 63 169 Oxford University 23 Page, Scott 137 Palacios — Huerta, I. 152 Paradis, J. 112 Paradox 10 19 137 139 143 171-72 Partial derivative 111 Partition-edit-count 152 Pascal, Blaise 9-12 Pascal’s triangle 11 Pearl, Judea 151 Peirce, Charles Sanders 16 Persian Gulf 31 PHD 2-3 25 29 Philosopher(s) viii 31 87 128 133 151 155 164-65 177 Physicist(s) 31 87 126-28 133 Piatelli — Palmarini, Massimo 31 Platters, silver 139 Possible outcomes 43-44 85 Posterior probability see Bayes’ Theorem Posterior uniformity 144 Prime number 46 Principle of non-arbitrariness 170-72 Prior probability see Bayes’ Theorem Prior uncertainty 104 Prisoners problem see Three prisoners problem Probabilistic weather forecasts 8 Probability calculations 37 43 probability distribution vii 44-46 49 50 55 59-63 122 Probability space 44 70 105 Probability theory, as an abstract construction 85 Probability theory, basics of 42-45 52 Probability theory, counterintuitive nature of 5-9 12 Probability theory, ecumenical view of 88 Probability theory, epistemic vs. statistical notions of 156-65 Probability theory, event, definition of 44 Probability theory, evidence and 7 14 Probability theory, exercises in 31 Probability theory, experiments in 4 28 40 58-59 64 85 87 122 Probability theory, history of 8-15 Probability theory, illustrating difficulty of 4-5 Probability theory, independence and 4 58-61 63 102 105 Probability theory, interpretations of 84-88 Probability theory, measures in 85 Probability theory, product rule and 6 60 63 Probability theory, reasoning about viii 5 9 Probability theory, single/individual cases and 160 164-65 Probability theory, sum rule and viii 4 44-45 Probability theory, textbooks on 85 121 139 Probability tree 53 76 131 169 Problem of points 10-12 Progressive Monty Hall problem, arbitrariness of door-numbering and 108 Progressive Monty Hall problem, basic principles of 98-101 Progressive Monty Hall problem, five-door case study of 95-101 Progressive Monty Hall problem, four-door version of 90-92 100 Progressive Monty Hall problem, information theory and see Information theory Progressive Monty Hall problem, Monty’s limitations and 89 Progressive Monty Hall problem, other switching strategies and 107-11 Progressive Monty Hall problem, probability vector and 96-99 101-2 Progressive Monty Hall problem, statement of 89 Progressive Monty Hall problem, switching at the last minute and 90 92-94 Progressive Monty Hall problem, switching every time and 92 105-7 Progressive Monty Hall problem, switching exactly 109-11 Progressive Monty Hall problem, unique optimality of SLM and 101-4 112 Proportionality principle 82-84 117 138 168-69 Prozac 9 Psychologists viii 7 41 87 128 PubMed database 133 Quantum information see Quantum mechanics Monty Quantum mechanics, irrational probabilities and 87 Quantum mechanics, Monty Hall problem and viii 126-28 Quantum mechanics, weirdness of 128 Quintuple 96 Radioactive 127 Random Monty 114 Random number generator 49 Random variables viii 122-23 162 Rao, M. Bhaskara 89 ratio 83 85 102 117 120-21 143 Rational number 43 87 96 Real numbers 85 Real-world situation 44 49 60 Recurrence relations ix 106-12 Refrigerators 123-124 Relative frequency 64 87 121 Risk and reward 81 Rolling dice see Dice rolling Rosenthal, Jeffrey 8 82-83 RRD-gnostic/agnostic condition 41 Russell, Bertrand 10 Sample space, definition of 44 Sample space, enumerating the elements of 10 11 18 21 27 45-46 52 58 66-67 89 Sample space, probability theory and vii 50 122 Sample space, subsets of 44 59 Sample space, two-child problem and 139-40 Scalpel 145 Scheherazade 39 Search engines 133 Self-information 105 Selvin, Steve 20-22 Sensory capacity 133 September 6 SEQUENCE 126 Sexually ambiguous children 148 Shannon, Claude viii 104-5 Shell game 27 144 Shimojo, S. 141-45 Single-case probability see Probability theory single/individual Skarsgard, Stellan 2 Sledgehammer 145 Slembeck, T. 152 Smith, John Maynard 18 Smullyan, Raymond 39-40 Some Teasers Concerning Conditional Probability 137 Spivey — Knowlton, M. 149 151 Sprenger, Jan 170 174 Stanford University 23 Statistical probability see Probability theory statistical Statisticians 31 87 140 Sticking argument/strategy 2-3 36 40 49-52 79 115 123-24 159 171 Stock, share of 136 Subatomic particle 127 Subjective probability 86 156 Subjective theorems 141-44 152 Sugar 71 Superposition of states 127-28 Supporters of switching 40 Surviving player 115-16 Sweden 146 Switching argument/strategy 2-3 36 38 48-52 75-76 80 159 Symmetry heuristic 145 System, physical 127 Takeichi, H. 148 Telegraph 105 Television 19 80 158 Textbooks, probability theory see Probability theory textbooks Theorem 85 110 112 142-43 Theoretical probability 50-51 64 Three prisoners problem 17-18 138 141-43 145 Three — Obsessed Monty 116-18 Todhunter, Isaac 13 Tossing coins see Coin tossing Trial and error 134 Tubau, E. 152 Two-ace problem 4 40 Two-child problem 138-40 Two-puppy problem 26 Tyran, J. 152 U. S. Department of Transportation 71 U. S. Open 22 Undergraduate course 12 Uniform distribution 59 Uniformity assumption 145 United States 146 Updated probability 70 82-84 94 101-2 117 139 Venn diagram 10 Venn, John 10 Ventoulias, A. 112 Verschueren, N. 152 Viader, P. 112 Vos Savant, Marilyn vii 23-31 130-31 141 144 Wang, X.T. 152 War (card game) 129 Whitaker, Craig 23 Wieth, Mareike 135 151 Wikipedia 52 113 Working memory capacity 153 Yale University 175 Zabell, Sandy 22 “And Behind Door Number One, a Fatal Flaw” 175 “Constant Ratio” theorem 142-43 “Essay Toward Solving a Problem in the Doctrine of Chances, An” 12 “Irrelevant, Therefore Invariant” theorem 142-43 “Number of Cases” theorem 142-43
Реклама
 |
|
О проекте
|
|
О проекте



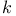 times and
times and