|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Friedman R., Morgan J.W. — Smooth four-manifolds and complex surfaces |
|
|
 |
| Предметный указатель |
#, connected sum of manifolds 12
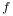 , fiber connected sum of , fiber connected sum of  elliptic surfaces 161 elliptic surfaces 161
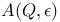 , the set of points a which satisfy , the set of points a which satisfy 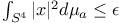 250 250
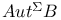 , the automorphisms of the elliptic surface B preserving the section , the automorphisms of the elliptic surface B preserving the section  76 76
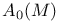 , automorphisms of the quadratic form of M which are the identity on all classes coming from the boundary 185 , automorphisms of the quadratic form of M which are the identity on all classes coming from the boundary 185
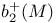 , dimension of a maximal positive definite subspace of , dimension of a maximal positive definite subspace of 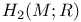 12 12
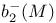 , dimension of a maximal negative definite subspace of , dimension of a maximal negative definite subspace of 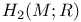 12 12
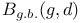 , the set of all surfaces S in B(g,d) such that , the set of all surfaces S in B(g,d) such that 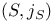 has generic branching behavior 64 has generic branching behavior 64
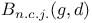 , the set of isomorphism classes of elliptic surfaces in B(g,d) with nonconstant j-invariant 63 , the set of isomorphism classes of elliptic surfaces in B(g,d) with nonconstant j-invariant 63
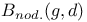 , the set of all surfaces S in B(g,d) such that S is nodal 64 , the set of all surfaces S in B(g,d) such that S is nodal 64
 , ,  261 261
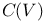 , elements of even or odd degree in C(V) 375 , elements of even or odd degree in C(V) 375
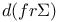 , the largest dimension of a stratum , the largest dimension of a stratum 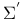 with with  261 261
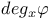 , local degree at x of the map , local degree at x of the map  whose differential at x is Fredholm of index zero 350 351 whose differential at x is Fredholm of index zero 350 351
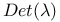 , determinant line bundle associated to , determinant line bundle associated to 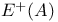 238 238
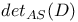 , the Atiyah — Singer determinant line bundle 385 , the Atiyah — Singer determinant line bundle 385
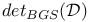 , the Bismut — Gillet — Soule determinant line bundle 391 , the Bismut — Gillet — Soule determinant line bundle 391
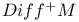 , group of orientation-preserving self-diffeomorphisms of M 12 , group of orientation-preserving self-diffeomorphisms of M 12
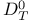 , the pullback of , the pullback of 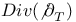 to to 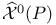 235 235
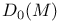 , the subgroup of D(M) induced by compactly supported orientation-preserving self-diffeomorphisms 185 , the subgroup of D(M) induced by compactly supported orientation-preserving self-diffeomorphisms 185
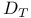 , the image of , the image of 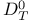 in in 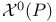 235 235
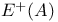 , the Atiyah — Hitchin — Singer deformation complex for the ASD connection A 237 , the Atiyah — Hitchin — Singer deformation complex for the ASD connection A 237
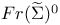 , the restriction of the fiber product over , the restriction of the fiber product over 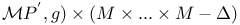 258 258
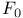 , union of the strata of , union of the strata of 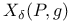 whose points have trivial background connections 263 whose points have trivial background connections 263
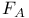 , the curvature of the connection A 232 , the curvature of the connection A 232
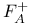 , the self-dual part of , the self-dual part of 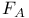 255 255
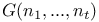 , the semi-direct product , the semi-direct product 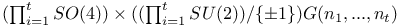 252 252
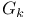 , the elements in , the elements in 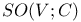 fixing fixing 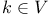 397 397
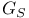 , the homological invariant of the elliptic surface S 43 , the homological invariant of the elliptic surface S 43
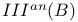 , the set of all elliptic surfaces without multiple fibers whose Jacobian surface is B 75 , the set of all elliptic surfaces without multiple fibers whose Jacobian surface is B 75
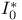 , a Kodaira fiber 60 , a Kodaira fiber 60
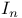 , a Kodaira fiber which is a cycle of n rational curves 51 52 , a Kodaira fiber which is a cycle of n rational curves 51 52
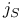 , the j-function of the elliptic surface S 43 , the j-function of the elliptic surface S 43
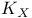 , the canonical bundle of the manifold X 11 , the canonical bundle of the manifold X 11
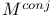 , the conjugate complex manifold corresponding to M 206 , the conjugate complex manifold corresponding to M 206
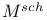 , scheme version of , scheme version of 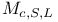 337 337
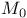 , , 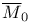 , deformation functors for stable or semistable bundles on C with trivial determinant 357 , deformation functors for stable or semistable bundles on C with trivial determinant 357
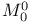 , , 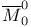 , rigidified versions of , rigidified versions of 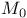 , , 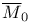 363 363
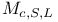 , global moduli functor of L-stable bundles on S with , global moduli functor of L-stable bundles on S with 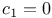 and and 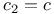 334 334
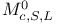 , based version of , based version of 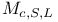 336 336
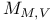 , global moduli functor of holomorphic structures on V 303 , global moduli functor of holomorphic structures on V 303
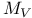 , local moduli functor of germs of deformations of V 304 , local moduli functor of germs of deformations of V 304
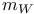 , multiplicity of the irreducible component W in the complex space Z 349 , multiplicity of the irreducible component W in the complex space Z 349
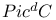 , the set of isomorphism classes of line bundles on C of degree d 11 , the set of isomorphism classes of line bundles on C of degree d 11
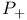 , projection onto the space of self-dual 2-forms 242 , projection onto the space of self-dual 2-forms 242
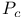 , the SU(2)-bundle over M with , the SU(2)-bundle over M with 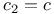 226 226
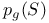 , the geometric genus of S 18 , the geometric genus of S 18
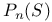 , the , the 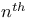 plurigenus of S 18 plurigenus of S 18
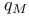 , intersection form of the oriented 4-manifold M 12 , intersection form of the oriented 4-manifold M 12
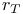 , restriction of connections to the 2-manifold T 234 , restriction of connections to the 2-manifold T 234
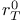 , restriction of connections for the quotient space of connections modulo the based gauge group 234 , restriction of connections for the quotient space of connections modulo the based gauge group 234
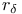 , reflection about , reflection about  185 185
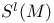 , the , the 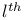 symmetric product of M 244 symmetric product of M 244
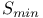 , the minimal model of the complex surface S 21 , the minimal model of the complex surface S 21
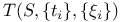 , set of elliptic surfaces locally isomorphic to S except over the , set of elliptic surfaces locally isomorphic to S except over the 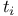 and with the same basic elliptic surface 102 and with the same basic elliptic surface 102
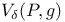 , thickened moduli space 247 257 , thickened moduli space 247 257
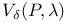 , parametrized version of , parametrized version of 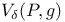 260 260
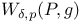 , subset of , subset of 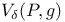 whose measures do not have singular support at p 257 whose measures do not have singular support at p 257
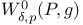 , based version of , based version of 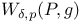 257 257
 , generalized connections with small curvature in a ball , generalized connections with small curvature in a ball 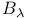 434 434
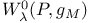 , based version of , based version of  435 435
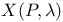 , parametrized version of X(P,g) 245 , parametrized version of X(P,g) 245
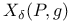 , thickened completion of the moduli space 260 , thickened completion of the moduli space 260
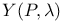 , , 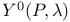 , parametrized versions of Y(P, g) and , parametrized versions of Y(P, g) and 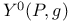 246 246
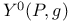 , a based version of Y(P, g) 246 , a based version of Y(P, g) 246
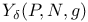 , set of points of , set of points of 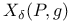 whose associated measures do not have support on N 263 whose associated measures do not have support on N 263
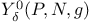 , based version of , based version of 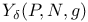 263 263
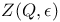 , the intersection of , the intersection of 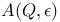 with the set of those points with the set of those points 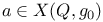 whose center of mass is the north pole 250 whose center of mass is the north pole 250
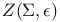 , , 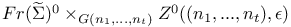 253 253
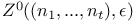 , ,  253 253
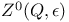 , based version of , based version of 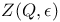 251 251
![$[\mathcal{M}(P,g)]_{\delta}$](/math_tex/eb9e6e993a9a8a97d69cd4c6fb9e799282.gif) , ,  -approximation to the fundamental class of -approximation to the fundamental class of 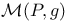 in in 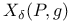 260 260
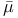 , extended , extended  -map 272 -map 272
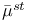 , extended , extended  -map defined on the stable elements 271 -map defined on the stable elements 271
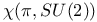 , character variety of representations of it in SU(2) 366 , character variety of representations of it in SU(2) 366
 -approximation to the fundamental class 260—262 -approximation to the fundamental class 260—262
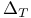 , smooth divisor representing , smooth divisor representing ![$\mu([T])$](/math_tex/7a9b6c945c5fa21a8707f01cacc5bdd582.gif) and lying in an arbitrarily small neighborhood of and lying in an arbitrarily small neighborhood of 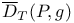 268 268
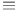 , linear equivalence of divisors 11 , linear equivalence of divisors 11
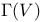 , group of units in , group of units in 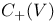 of norm one 375 of norm one 375
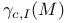 , generalized Donaldson polynomial for M 411 412 , generalized Donaldson polynomial for M 411 412
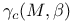 , restricted Donaldson polynomial for M 278 , restricted Donaldson polynomial for M 278
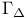 , group generated by the reflections in the set , group generated by the reflections in the set  185 401 185 401
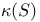 , the Kodaira dimension of S 19 , the Kodaira dimension of S 19
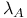 , the operator , the operator 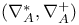 238 238
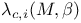 , coefficients of the dual element to , coefficients of the dual element to 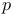 in the expansion of in the expansion of 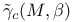 278 278
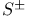 , the bundles of plus and minus spinors 235 376 , the bundles of plus and minus spinors 235 376
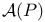 , space of all irreducible , space of all irreducible 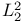 connections on the principal bundle P 231 connections on the principal bundle P 231
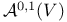 , space of all simple , space of all simple 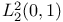 -connections on the vector bundle V 293 -connections on the vector bundle V 293
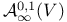 , space of all simple , space of all simple 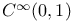 -connections on the vector bundle V 283 -connections on the vector bundle V 283
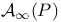 , space of all irreducible , space of all irreducible  connections on the principal bundle P 230 connections on the principal bundle P 230
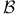 , sheaf of holomorphic cross-sections of the elliptic surface B 77 , sheaf of holomorphic cross-sections of the elliptic surface B 77
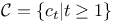 , group of conformal contractions of , group of conformal contractions of 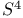 251 251
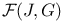 , the set of elliptic surfaces without multiple fibers with the invariants J and G 76 , the set of elliptic surfaces without multiple fibers with the invariants J and G 76
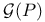 , the , the 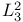 -gauge group of the bundle F 231 -gauge group of the bundle F 231
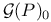 , the based gauge group of the bundle F 233 , the based gauge group of the bundle F 233
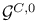 , the , the 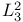 based complex gauge group 330 based complex gauge group 330
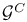 , the , the 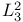 complex gauge group 293 complex gauge group 293
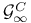 , the complex gauge group of , the complex gauge group of  bundle isomorphisms of the vector bundle V 285 bundle isomorphisms of the vector bundle V 285
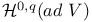 , , 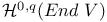 , harmonic forms for the elliptic complex , harmonic forms for the elliptic complex 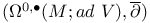 or or 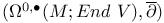 294 294
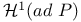 , ,  , harmonic forms for the elliptic complex , harmonic forms for the elliptic complex 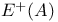 324 324
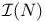 , generalized connections whose singular support meets N 263 , generalized connections whose singular support meets N 263
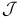 , the subsheaf of , the subsheaf of 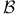 consisting of holomorphic sections of consisting of holomorphic sections of  passing through the identity components of the reducible fibers 82 passing through the identity components of the reducible fibers 82
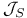 , the sheaf , the sheaf 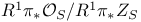 on the elliptic surface S 85 on the elliptic surface S 85
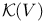 , the Kuranishi model for the space of deformations of the complex structure on V 295 , the Kuranishi model for the space of deformations of the complex structure on V 295
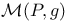 , the moduli space of all irreducible g-ASD connections on P modulo gauge equivalence 236 , the moduli space of all irreducible g-ASD connections on P modulo gauge equivalence 236
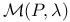 , the parametrized moduli space of all , the parametrized moduli space of all 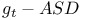 connections on P where connections on P where  is the path is the path 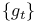 239 239
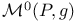 , the based moduli space of all g-ASD connections on P 237 , the based moduli space of all g-ASD connections on P 237
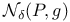 , the image of , the image of 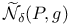 in in 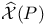 256 256
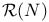 , reducible ASD connections on the negative definite manifold N 431 , reducible ASD connections on the negative definite manifold N 431
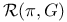 , variety of representations of n in the Lie group G 366 , variety of representations of n in the Lie group G 366
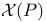 , space of irreducible , space of irreducible 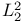 connections on P modulo gauge equivalence 232 connections on P modulo gauge equivalence 232
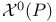 , , 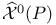 , based versions of , based versions of 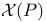 and and 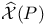 233 233
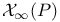 , space of irreducible , space of irreducible  connections on P modulo gauge equivalence 230 connections on P modulo gauge equivalence 230
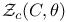 , the divisor on , the divisor on 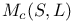 corresponding to the smooth curve corresponding to the smooth curve 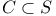 and the theta characteristic and the theta characteristic  on C 344 345 on C 344 345
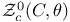 , the divisor , the divisor 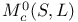 corresponding to corresponding to 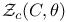 344 344
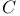 , universal elliptic curve over , universal elliptic curve over 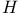 37 37
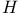 , the upper half plane 36 , the upper half plane 36
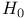 , , 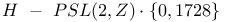 40 40
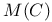 , moduli space of stable bundles of degree zero on C 356 , moduli space of stable bundles of degree zero on C 356
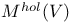 , the set of simple holomorphic structures on V 294 , the set of simple holomorphic structures on V 294
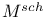 , scheme version of , scheme version of 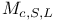 337 337
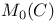 , subset of , subset of 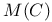 of bundles with trivial determinant 356 of bundles with trivial determinant 356
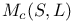 , the moduli space of L-stable rank two holomorphic bundles with , the moduli space of L-stable rank two holomorphic bundles with 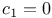 and and 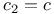 328 328
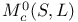 , the based moduli space corresponding to , the based moduli space corresponding to 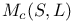 330 330
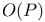 , , 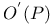 , sets of generic metrics 237 249 , sets of generic metrics 237 249
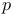 , the image of 1 under the , the image of 1 under the  -map 269 -map 269
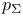 , the restriction of the extension of , the restriction of the extension of 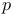 to a stratum to a stratum  270 270
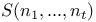 , the largest subgroup of the permutation group of the factors preserving the multiplicities 252 , the largest subgroup of the permutation group of the factors preserving the multiplicities 252
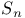 , the symmetric group on n letters 68 , the symmetric group on n letters 68
 , universal cover of neighborhood of a , universal cover of neighborhood of a 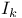 fiber 54 fiber 54
 -map 226—229 233—235 340—345 370 371 374 428—431 433 444 461 477—479 486 487 490 -map 226—229 233—235 340—345 370 371 374 428—431 433 444 461 477—479 486 487 490
 -map, extension of 228 263—273 -map, extension of 228 263—273
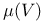 , normalized degree or slope of the holomorphic bundle V with respect to a fixed Kaehler class or ample line bundle 322 , normalized degree or slope of the holomorphic bundle V with respect to a fixed Kaehler class or ample line bundle 322
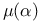 , the map , the map 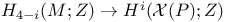 defined by slant product defined by slant product 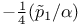 233 233
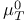 , SO(3)-equivariant class in , SO(3)-equivariant class in 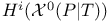 , where T is an embedded 2-manifold 235 , where T is an embedded 2-manifold 235
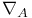 , differential operator associated to the connection A 231 , differential operator associated to the connection A 231
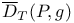 , the subset of , the subset of 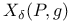 such that either the background connection lies in such that either the background connection lies in 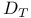 or the singular support meets T 268 or the singular support meets T 268
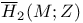 , , 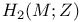 /Torsion 12 /Torsion 12
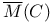 , compact moduli space of equivalence classes of semistable bundles of degree zero on C 357 , compact moduli space of equivalence classes of semistable bundles of degree zero on C 357
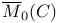 , subset of , subset of 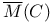 of bundles with trivial determinant 357 of bundles with trivial determinant 357
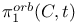 , the orbifold fundamental group of C 145 , the orbifold fundamental group of C 145
 , the real spinor norm 397 , the real spinor norm 397
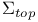 , the top stratum , the top stratum 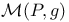 of X(P,g) 261 of X(P,g) 261
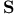 , all complex surfaces S such that , all complex surfaces S such that 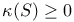 or or 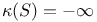 and S is algebraic or is deformation equivalent to a (possibly blown up) Hopf surface 221 and S is algebraic or is deformation equivalent to a (possibly blown up) Hopf surface 221
 , the theta divisor of a Jacobian 345 , the theta divisor of a Jacobian 345
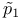 , first Pontrjagin class of the universal SO(3) bundle over , first Pontrjagin class of the universal SO(3) bundle over 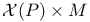 232 232
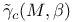 , Donaldson polynomial for M 226 277 , Donaldson polynomial for M 226 277
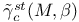 , stable Donaldson polynomial for M 271 273 , stable Donaldson polynomial for M 271 273
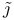 , the classical j-function on the upper half plane 37 , the classical j-function on the upper half plane 37
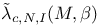 , generalized polynomial invariants arising from the connected sum with the negative definite manifold N 426 , generalized polynomial invariants arising from the connected sum with the negative definite manifold N 426
| 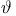 , a theta function with characteristic 345 , a theta function with characteristic 345
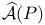 , space of all , space of all 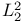 connections on the principal bundle P 230 connections on the principal bundle P 230
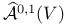 , space of all , space of all 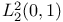 -connections on the vector bundle V 293 -connections on the vector bundle V 293
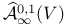 , space of all , space of all 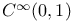 -connections on the vector bundle V 283 -connections on the vector bundle V 283
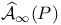 , space of all , space of all  connections on the principal bundle P 230 connections on the principal bundle P 230
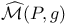 , the moduli space of all g-ASD connections on P modulo gauge equivalence 236 , the moduli space of all g-ASD connections on P modulo gauge equivalence 236
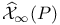 , space of all , space of all 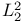 connections on P modulo gauge equivalence 231 connections on P modulo gauge equivalence 231
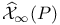 , space of all connections on P modulo gauge equivalence 230 , space of all connections on P modulo gauge equivalence 230
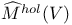 , the set of all holomorphic structures on V (usually assumed to have trivial determinant) 285 , the set of all holomorphic structures on V (usually assumed to have trivial determinant) 285
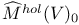 , the set of holomorphic structures on V with trivial determinant 301 , the set of holomorphic structures on V with trivial determinant 301
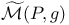 , the moduli space of all g-ASD connections on P 236 , the moduli space of all g-ASD connections on P 236
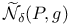 , almost ASD connections on P which are almost flat away from certain points of concentrated curvature, and which lie in the span of the eigenvectors with small eigenvalues for the operator , almost ASD connections on P which are almost flat away from certain points of concentrated curvature, and which lie in the span of the eigenvectors with small eigenvalues for the operator 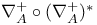 255 255
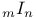 , a multiple fiber whose reduction is a cycle of n rational curves 35 , a multiple fiber whose reduction is a cycle of n rational curves 35
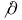 , the Dirac operator 235 , the Dirac operator 235
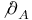 , the Dirac operator coupled to the connection A 235 , the Dirac operator coupled to the connection A 235
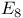 , the intersection form corresponding to the negative of the matrix for the root system , the intersection form corresponding to the negative of the matrix for the root system 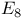 180 180
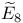 , the intersection form corresponding to the negative of the matrix for the extended root system , the intersection form corresponding to the negative of the matrix for the extended root system 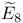 181 182 181 182
A(M), automorphisms of 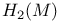 preserving the quadratic form preserving the quadratic form 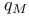 of M 12 of M 12
A(M, k), automorphisms of the quadratic form of M preserving k 393
ad P, adjoint bundle associated to the principal bundle P 230
ad V, vector bundle of trace zero endomorphisms of the vector bundle V 300
Adjunction formula 194 418 454 464
Almost complex structure 282 284 308 312—313 314
Analytic function on a Banach space 285—293
Anti-self dual (ASD) see "Connection anti-self-dual"
Artin ring 95 337 350
Artin, M. 32
ASD connections see "Connection anti-self-dual"
ASD Yang — Mills equations see "Yang — Mills equations"
Atiyah — Hitchin — Singer deformation complex 237 319
Atiyah — Singer determinant see "Determinant line bundle Atiyah
Atiyah's theorem on vector bundles over elliptic curves 447 448 452 456
Atiyah, M. 137
Averbuh, B.G. 32
B(g,d), the set of isomorphism classes of elliptic surfaces S with a section with Euler number 12d over a base of genus g 63
Background connection 228 229 244—247 249—251 253—255 257—261 263 265 266 430 434—436
Base change 33 38 47 53 95 98 99 115 116 163 164 338 382 452 462 465 466 482 483 488
Basic member 76 85 93 205
Basic surface see "Elliptic surface basic"
Bauer, S. 223 497
Bianchi identity 284 294
Bismut — Freed determinant 374
Bismut — Gillet — Soule determinant 374 389—392
Block 71—75
Blowing down 17 21 24—27
Blowing down in families 21 24—27 35
Blowing up 17 19 131 132 163
Blowup 4 5 10 17—20 23 27 28 36 51 59 131 132 137 154—157 163 164 181 221—225 394 411—416 418 426 491—498
Bogomolov — Miyaoka — Yau inequality 30 494 495
Bogomolov's inequality 367
Bogomolov, F. 366
Bombieri's theorem on the canonical map 33
Bombieri, E. 33
Borel measure 240
Botany 23
Bott, R. 137
Bounded homogeneous polynomial 285
Br B, the Brauer group of B 86
Brauer group 86 109 335
Bridge 72—75
Brieskorn, E. 33 115
Brussee, R. 499
C(V), Clifford algebra of V 374
c-generic 339
c-stable 271 276
c-suitable 436 438 446—448 450 451 453 454 468 476 477
Canonical bundle 2 10 11 16—20 24 25 130 160 341 343 376 394 406 410 418 450 477
Canonical bundle formula for an elliptic surface 16 36 49 50 129 130 454 464 475
Cartan matrix 179 187
Cartan's privileged neighborhood theorem 298
Case (A) 447 448 451 453—455 469 479 480 485 497
Case (B) 448 453—456 480 481
Castelnuovo — deFranchis theorem 20 30 494
Castelnuovo — Enriques theorem 20
Castelnuovo's theorem 2 25
Categorical quotient 362 364
Christoffel symbol 378
Clifford algebra 374 375
Clifford multiplication 375—377
Clifford's theorem 360
Closure of modules theorem 288 289
Compatible lift 41—47 67
Completion of the moduli space 239—246
Completion of the moduli space, thickened 247 260—263
Complex space 11
Complex space, defined by a Fredholm map 290—293
Complex space, defined by a Fredholm section 265 292 293
Complex torus 22 30—33 92 131 154 155 199 209 214 222 224 444 458 494 495
Cone bundle 228 247 251 253 255 258—260 265 271
Cone structure 248 251 253 258
Conformal length 432
Conjugate complex manifold 5 139 206 409
Connected sum 2 9 10 12 161 229 271 356 394 411—414 416—419 425 426 432 433 435
Connection, (0,1)- 283—285 294 300 301 307 314 324 327 331
Connection, background 228 229 244—247 249—251 253—255 257—261 263 265 266 430 434—436
Connection, compatible with the complex structure 280—283 313 320 323 333
Connection, Ehresmann 280 284 314
Connection, flat 88 249 251 366 369 379
Connection, Hermite — Einstein 323
Connection, Hermitian 281 323
Connection, integrable 284 285
Connection, irreducible 226 227 230 231 234 236 237 249 256 271 279 324—327 330 347 365 429 431 438
Connection, Levi-Civita 376
Connection, product 240 243 249 256 258
Connection, reducible 231 246 249 250 257 274 338 348 366 429—432 436 438—440
Connection, trivial 228 238 243 246 247 255—260 348 370 373 430 431 433 435
Connections, based, space of gauge equivalence classes 233 431
Connections, space of gauge equivalence classes 226 230—234
Contains in the sense of complex spaces 288
Curvature 230 232 282 283
Curvature, (0,2)- 284 285 293
Curvature, concentrated 228 254
Cyclic monodromy 195—197 201 202 205 209 210 214 215
d(c), one-half the expected dimension of the moduli space, namely 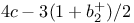 226 226
D(M), the subgroup of A(M) induced by 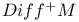 12 12
D(M,k), the subgroup of D(M) of elements fixing k 393 405
D*(M), the subgroup of D(M) of elements of real spinor norm one 393
Dabrowski, K. 133
Deformation equivalence 4 5 10 14—22 25 28 29 31—34 57 61 81 93 103 138—140 157 201 221—224 409 442 445 497
Deformation equivalence through elliptic surfaces 35 57 64—67 79 81 82 103—107 110—132 158 159 201 205—209 211 215
Deformation invariance of Kodaira dimension 20 26 27
Deformation invariance of the plurigenera 20 24 26 27 128—130
Deformation type 4—7 16 17 28 195 497
Deformation, unobstructed 301
Degree, local, for a Fredholm map of index zero 352 355
Dehn twist 167
Dehn — Nielsen theorem 146—154
Deligne — Mumford Theorem 125
Deligne, P. 401
Descent conditions 473
det 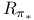 , the holomorphic determinant line bundle 383 , the holomorphic determinant line bundle 383
Determinant line bundle 238 340 352 355 374
Determinant line bundle, Atiyah — Singer 235 374 385—389 391
Determinant line bundle, Bismut — Freed 374
Determinant line bundle, Bismut — Gillet — Soule 374 389—392
Determinant line bundle, holomorphic 341 342 344 364 366 374 379—385 387—389 391
Diffeomorphism group, big 9 393 394 405—409 413 415 416 418 420 425 427 490 499
Diffeomorphism group, big, Donaldson polynomial of a 4-manifold with 9 393 406—408 490 499
Dirac operator 235 268 269 274 340 341 346—348 374—379
Directional derivative 420
Distribution, horizontal 232 280 282 331
Distribution, integrable 308
Distribution, involutive 308
Div, div, the zero set of the natural section of the inverse of the determinant line bundle 384
Dolgachev, I. 16 75 86
Donaldson polynomial invariant 4 226 227
Donaldson polynomial invariant, full 229 230 276 278
Donaldson polynomial invariant, generalized 411—413
Donaldson polynomial invariant, restricted 278
Donaldson polynomial invariant, stable 229 271—273 276
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



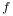 , fiber connected sum of
, fiber connected sum of  elliptic surfaces
elliptic surfaces 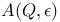 , the set of points a which satisfy
, the set of points a which satisfy 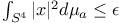
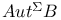 , the automorphisms of the elliptic surface B preserving the section
, the automorphisms of the elliptic surface B preserving the section 
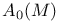 , automorphisms of the quadratic form of M which are the identity on all classes coming from the boundary
, automorphisms of the quadratic form of M which are the identity on all classes coming from the boundary 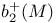 , dimension of a maximal positive definite subspace of
, dimension of a maximal positive definite subspace of 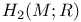
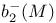 , dimension of a maximal negative definite subspace of
, dimension of a maximal negative definite subspace of 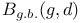 , the set of all surfaces S in B(g,d) such that
, the set of all surfaces S in B(g,d) such that 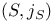 has generic branching behavior
has generic branching behavior 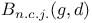 , the set of isomorphism classes of elliptic surfaces in B(g,d) with nonconstant j-invariant
, the set of isomorphism classes of elliptic surfaces in B(g,d) with nonconstant j-invariant 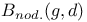 , the set of all surfaces S in B(g,d) such that S is nodal
, the set of all surfaces S in B(g,d) such that S is nodal  ,
, 
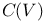 , elements of even or odd degree in C(V)
, elements of even or odd degree in C(V) 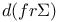 , the largest dimension of a stratum
, the largest dimension of a stratum 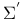 with
with 
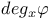 , local degree at x of the map
, local degree at x of the map  whose differential at x is Fredholm of index zero
whose differential at x is Fredholm of index zero 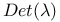 , determinant line bundle associated to
, determinant line bundle associated to 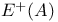
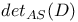 , the Atiyah — Singer determinant line bundle
, the Atiyah — Singer determinant line bundle 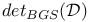 , the Bismut — Gillet — Soule determinant line bundle
, the Bismut — Gillet — Soule determinant line bundle 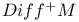 , group of orientation-preserving self-diffeomorphisms of M
, group of orientation-preserving self-diffeomorphisms of M 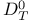 , the pullback of
, the pullback of 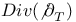 to
to 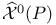
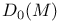 , the subgroup of D(M) induced by compactly supported orientation-preserving self-diffeomorphisms
, the subgroup of D(M) induced by compactly supported orientation-preserving self-diffeomorphisms 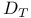 , the image of
, the image of 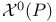
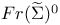 , the restriction of the fiber product over
, the restriction of the fiber product over 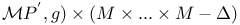
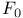 , union of the strata of
, union of the strata of 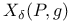 whose points have trivial background connections
whose points have trivial background connections 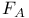 , the curvature of the connection A
, the curvature of the connection A 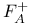 , the self-dual part of
, the self-dual part of 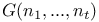 , the semi-direct product
, the semi-direct product 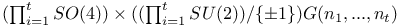
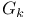 , the elements in
, the elements in 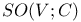 fixing
fixing 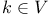
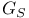 , the homological invariant of the elliptic surface S
, the homological invariant of the elliptic surface S 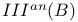 , the set of all elliptic surfaces without multiple fibers whose Jacobian surface is B
, the set of all elliptic surfaces without multiple fibers whose Jacobian surface is B 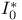 , a Kodaira fiber
, a Kodaira fiber 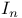 , a Kodaira fiber which is a cycle of n rational curves
, a Kodaira fiber which is a cycle of n rational curves 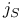 , the j-function of the elliptic surface S
, the j-function of the elliptic surface S 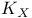 , the canonical bundle of the manifold X
, the canonical bundle of the manifold X 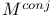 , the conjugate complex manifold corresponding to M
, the conjugate complex manifold corresponding to M 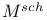 , scheme version of
, scheme version of 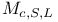
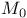 ,
, 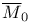 , deformation functors for stable or semistable bundles on C with trivial determinant
, deformation functors for stable or semistable bundles on C with trivial determinant 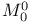 ,
, 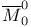 , rigidified versions of
, rigidified versions of 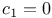 and
and 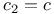
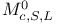 , based version of
, based version of 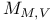 , global moduli functor of holomorphic structures on V
, global moduli functor of holomorphic structures on V 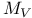 , local moduli functor of germs of deformations of V
, local moduli functor of germs of deformations of V 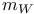 , multiplicity of the irreducible component W in the complex space Z
, multiplicity of the irreducible component W in the complex space Z 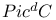 , the set of isomorphism classes of line bundles on C of degree d
, the set of isomorphism classes of line bundles on C of degree d 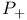 , projection onto the space of self-dual 2-forms
, projection onto the space of self-dual 2-forms 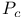 , the SU(2)-bundle over M with
, the SU(2)-bundle over M with 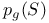 , the geometric genus of S
, the geometric genus of S 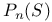 , the
, the 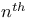 plurigenus of S
plurigenus of S 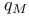 , intersection form of the oriented 4-manifold M
, intersection form of the oriented 4-manifold M 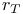 , restriction of connections to the 2-manifold T
, restriction of connections to the 2-manifold T 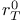 , restriction of connections for the quotient space of connections modulo the based gauge group
, restriction of connections for the quotient space of connections modulo the based gauge group 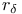 , reflection about
, reflection about 
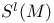 , the
, the 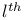 symmetric product of M
symmetric product of M 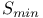 , the minimal model of the complex surface S
, the minimal model of the complex surface S 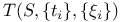 , set of elliptic surfaces locally isomorphic to S except over the
, set of elliptic surfaces locally isomorphic to S except over the 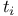 and with the same basic elliptic surface
and with the same basic elliptic surface 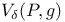 , thickened moduli space
, thickened moduli space 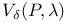 , parametrized version of
, parametrized version of 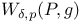 , subset of
, subset of 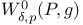 , based version of
, based version of  , generalized connections with small curvature in a ball
, generalized connections with small curvature in a ball 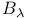
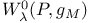 , based version of
, based version of 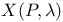 , parametrized version of X(P,g)
, parametrized version of X(P,g) 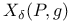 , thickened completion of the moduli space
, thickened completion of the moduli space 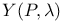 ,
, 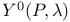 , parametrized versions of Y(P, g) and
, parametrized versions of Y(P, g) and 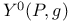
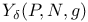 , set of points of
, set of points of 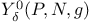 , based version of
, based version of 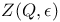 , the intersection of
, the intersection of 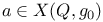 whose center of mass is the north pole
whose center of mass is the north pole 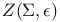 ,
, 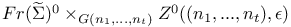
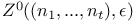 ,
, 
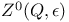 , based version of
, based version of ![$[\mathcal{M}(P,g)]_{\delta}$](/math_tex/eb9e6e993a9a8a97d69cd4c6fb9e799282.gif) ,
, 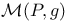 in
in 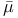 , extended
, extended  -map
-map 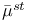 , extended
, extended 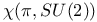 , character variety of representations of it in SU(2)
, character variety of representations of it in SU(2) 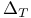 , smooth divisor representing
, smooth divisor representing ![$\mu([T])$](/math_tex/7a9b6c945c5fa21a8707f01cacc5bdd582.gif) and lying in an arbitrarily small neighborhood of
and lying in an arbitrarily small neighborhood of 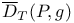
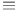 , linear equivalence of divisors
, linear equivalence of divisors 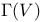 , group of units in
, group of units in 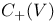 of norm one
of norm one 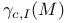 , generalized Donaldson polynomial for M
, generalized Donaldson polynomial for M 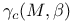 , restricted Donaldson polynomial for M
, restricted Donaldson polynomial for M 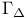 , group generated by the reflections in the set
, group generated by the reflections in the set 
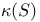 , the Kodaira dimension of S
, the Kodaira dimension of S 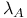 , the operator
, the operator 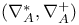
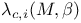 , coefficients of the dual element to
, coefficients of the dual element to 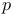 in the expansion of
in the expansion of 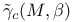
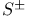 , the bundles of plus and minus spinors
, the bundles of plus and minus spinors 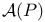 , space of all irreducible
, space of all irreducible 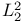 connections on the principal bundle P
connections on the principal bundle P 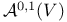 , space of all simple
, space of all simple 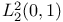 -connections on the vector bundle V
-connections on the vector bundle V 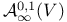 , space of all simple
, space of all simple 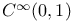 -connections on the vector bundle V
-connections on the vector bundle V 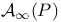 , space of all irreducible
, space of all irreducible 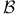 , sheaf of holomorphic cross-sections of the elliptic surface B
, sheaf of holomorphic cross-sections of the elliptic surface B 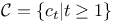 , group of conformal contractions of
, group of conformal contractions of 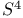
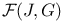 , the set of elliptic surfaces without multiple fibers with the invariants J and G
, the set of elliptic surfaces without multiple fibers with the invariants J and G 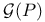 , the
, the 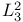 -gauge group of the bundle F
-gauge group of the bundle F 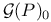 , the based gauge group of the bundle F
, the based gauge group of the bundle F 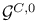 , the
, the 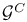 , the
, the 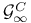 , the complex gauge group of
, the complex gauge group of 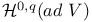 ,
, 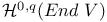 , harmonic forms for the elliptic complex
, harmonic forms for the elliptic complex 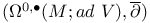 or
or 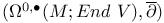
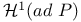 ,
,  , harmonic forms for the elliptic complex
, harmonic forms for the elliptic complex 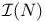 , generalized connections whose singular support meets N
, generalized connections whose singular support meets N 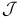 , the subsheaf of
, the subsheaf of  passing through the identity components of the reducible fibers
passing through the identity components of the reducible fibers 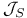 , the sheaf
, the sheaf 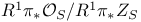 on the elliptic surface S
on the elliptic surface S 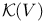 , the Kuranishi model for the space of deformations of the complex structure on V
, the Kuranishi model for the space of deformations of the complex structure on V 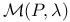 , the parametrized moduli space of all
, the parametrized moduli space of all 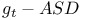 connections on P where
connections on P where  is the path
is the path 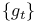
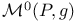 , the based moduli space of all g-ASD connections on P
, the based moduli space of all g-ASD connections on P 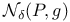 , the image of
, the image of 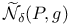 in
in 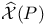
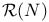 , reducible ASD connections on the negative definite manifold N
, reducible ASD connections on the negative definite manifold N 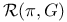 , variety of representations of n in the Lie group G
, variety of representations of n in the Lie group G 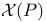 , space of irreducible
, space of irreducible 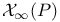 , space of irreducible
, space of irreducible 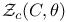 , the divisor on
, the divisor on 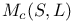 corresponding to the smooth curve
corresponding to the smooth curve 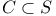 and the theta characteristic
and the theta characteristic  on C
on C 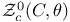 , the divisor
, the divisor 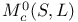 corresponding to
corresponding to 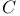 , universal elliptic curve over
, universal elliptic curve over 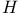
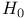 ,
, 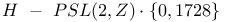
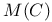 , moduli space of stable bundles of degree zero on C
, moduli space of stable bundles of degree zero on C 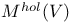 , the set of simple holomorphic structures on V
, the set of simple holomorphic structures on V 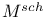 , scheme version of
, scheme version of 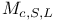
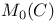 , subset of
, subset of 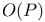 ,
, 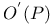 , sets of generic metrics
, sets of generic metrics 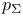 , the restriction of the extension of
, the restriction of the extension of 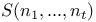 , the largest subgroup of the permutation group of the factors preserving the multiplicities
, the largest subgroup of the permutation group of the factors preserving the multiplicities 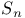 , the symmetric group on n letters
, the symmetric group on n letters  , universal cover of neighborhood of a
, universal cover of neighborhood of a 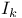 fiber
fiber 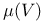 , normalized degree or slope of the holomorphic bundle V with respect to a fixed Kaehler class or ample line bundle
, normalized degree or slope of the holomorphic bundle V with respect to a fixed Kaehler class or ample line bundle 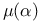 , the map
, the map 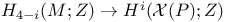 defined by slant product
defined by slant product 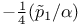
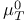 , SO(3)-equivariant class in
, SO(3)-equivariant class in 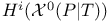 , where T is an embedded 2-manifold
, where T is an embedded 2-manifold 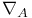 , differential operator associated to the connection A
, differential operator associated to the connection A 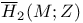 ,
, 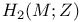 /Torsion
/Torsion 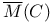 , compact moduli space of equivalence classes of semistable bundles of degree zero on C
, compact moduli space of equivalence classes of semistable bundles of degree zero on C 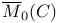 , subset of
, subset of 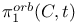 , the orbifold fundamental group of C
, the orbifold fundamental group of C  , the real spinor norm
, the real spinor norm 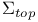 , the top stratum
, the top stratum 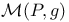 of X(P,g)
of X(P,g) 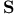 , all complex surfaces S such that
, all complex surfaces S such that 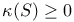 or
or 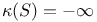 and S is algebraic or is deformation equivalent to a (possibly blown up) Hopf surface
and S is algebraic or is deformation equivalent to a (possibly blown up) Hopf surface  , the theta divisor of a Jacobian
, the theta divisor of a Jacobian 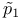 , first Pontrjagin class of the universal SO(3) bundle over
, first Pontrjagin class of the universal SO(3) bundle over 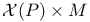
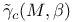 , Donaldson polynomial for M
, Donaldson polynomial for M 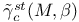 , stable Donaldson polynomial for M
, stable Donaldson polynomial for M 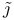 , the classical j-function on the upper half plane
, the classical j-function on the upper half plane 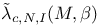 , generalized polynomial invariants arising from the connected sum with the negative definite manifold N
, generalized polynomial invariants arising from the connected sum with the negative definite manifold N 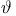 , a theta function with characteristic
, a theta function with characteristic 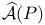 , space of all
, space of all 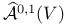 , space of all
, space of all 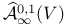 , space of all
, space of all 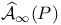 , space of all
, space of all 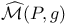 , the moduli space of all g-ASD connections on P modulo gauge equivalence
, the moduli space of all g-ASD connections on P modulo gauge equivalence 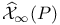 , space of all
, space of all 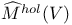 , the set of all holomorphic structures on V (usually assumed to have trivial determinant)
, the set of all holomorphic structures on V (usually assumed to have trivial determinant) 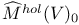 , the set of holomorphic structures on V with trivial determinant
, the set of holomorphic structures on V with trivial determinant 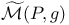 , the moduli space of all g-ASD connections on P
, the moduli space of all g-ASD connections on P 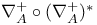
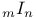 , a multiple fiber whose reduction is a cycle of n rational curves
, a multiple fiber whose reduction is a cycle of n rational curves 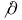 , the Dirac operator
, the Dirac operator 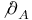 , the Dirac operator coupled to the connection A
, the Dirac operator coupled to the connection A 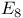 , the intersection form corresponding to the negative of the matrix for the root system
, the intersection form corresponding to the negative of the matrix for the root system 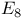
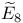 , the intersection form corresponding to the negative of the matrix for the extended root system
, the intersection form corresponding to the negative of the matrix for the extended root system 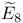
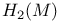 preserving the quadratic form
preserving the quadratic form 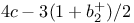
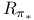 , the holomorphic determinant line bundle
, the holomorphic determinant line bundle