Miron R. — The Geometry of Higher-Order Lagrange Spaces: Applications to Mechanics and Physics (Fundamental Theories of Physics) :: Электронная библиотека попечительского совета мехмата МГУ

Главная Ex Libris Книги Журналы Статьи Серии Каталог Wanted Загрузка ХудЛит Справка Поиск по индексам Поиск Форум

Авторизация

Поиск по указателям

Miron R. — The Geometry of Higher-Order Lagrange Spaces: Applications to Mechanics and Physics (Fundamental Theories of Physics)

Обсудите книгу на научном форуме

Нашли опечатку?
Выделите ее мышкой и нажмите Ctrl+Enter

Название: The Geometry of Higher-Order Lagrange Spaces: Applications to Mechanics and Physics (Fundamental Theories of Physics)

Автор: Miron R.

Аннотация:

This monograph is devoted to the problem of the geometrizing of Lagrangians which depend on higher-order accelerations. It presents a construction of the geometry of the total space of the bundle of the accelerations of order k>=1. A geometrical study of the notion of the higher-order Lagrange space is conducted, and the old problem of prolongation of Riemannian spaces to k-osculator manifolds is solved. Also, the geometrical ground for variational calculus on the integral of actions involving higher-order Lagrangians is dealt with. Applications to higher-order analytical mechanics and theoretical physics are included as well. Audience: This volume will be of interest to scientists whose work involves differential geometry, mechanics of particles and systems, calculus of variation and optimal control, optimization, optics, electromagnetic theory, and biology.

Язык:

Рубрика: Математика/

Статус предметного указателя: Готов указатель с номерами страниц

ed2k: ed2k stats

Издание: 1st

Год издания: 1997

Количество страниц: 333

Добавлена в каталог: 03.01.2014

Операции: Положить на полку | Скопировать ссылку для форума | Скопировать ID

Предметный указатель

Absolute Energy      39
Action integral      26
Almost (k-1)n-contact model      183
Almost (k-1)n-contact structure      70 178
Almost Hermitian structure      41
Almost Kaehalerian model      40
Almost product structure      70
Atlas      47
Basis, adapted      60 169
Basis, local      50 160
Berwald connection      14 188
Bianchi identities      19 255
Bundle k-osculator      46 155
Bundle, principal      288
Canonical N-connection      152
Canonical spray      134
Coefficients of a non-linear connection      58
Coefficients of an N-linear connection      82 187
Coefficients, dual of a non-linear connection      62
Connection of Berwald type      83
Connection, N-linear      78
Connection, nonlinear      56
Coordinates of a point      47
Coordinates, transformation of      47
Covariant derivatives h- and 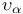$\upsilon_{\alpha}$ -      84
Curvature of an N-linear connection      193
D-vector      61
D-vector, d-tensor      75 182
D-vector, Liouville d-vector      68
Deflection tensors      84 189
Distribution, horizontal      57 165
Distribution, J-vertical      59 168
Distribution, vertical      49 159
Einstein equations      258
Einstein — Yang — Mills equations      308
Electromagnetic tensor fields      261
Energies of superior order      214
Euler — Lagrange equation      146
Extremal curves      27
Fibre bundle      287
Finsler spaces      36
Fundamental tensor of a Finsler space      36
Fundamental tensor of a higher order Lagrange space      245
Fundamental tensor of a Lagrange space      25
Gauge invariance      306
Gauge k-osculator bundle      289

Gauge N-linear connection      301
Gauge transformation      288
Gauss — Codazzi equations      284
Gauss — Weingarten formulae      282
Generalized Lagrange space of order k      262
Hamilton — Jacobi equations      130 223
Higher order Lagrange space      246
Induced nonlinear connection      273
Induced normal connection      279
Induced tangent connection      278
Integral of action      207
Jacobi — Ostrogradski momenta      128
Lagrangian of higher order      205
Lagrangian, differentiable      205
Lagrangian, regular      206
Lagrangian, subspaces of order k      271
Lift horizontal      166
Liouville d-vector fields      174
Liouville vector fields      161
Main invariants      207
Maxwell equations      261
Metric structure      183
Moving frame      272
N-linear connection      187
Nonlinear connection      165
Presymplectic structure      131
Projector, horizontal      166
Projector, vertical      166
Prolongation of Finslerian structure      235
Prolongation of Riemannian structure      229
Pull-back      56
Reducible to      263
Relativ covariant derivative      280
Ricci identities      93
Second fundamental tensors      282
Sections in 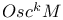$Osc^{k}M$       47
Sequence, exact      56
Sequence, splitting      56
Spray      5
Spray, k-spray      162
Structure equations      201
Torsion, h-torsion      193
Torsion, ua-torsion      193
Total derivative      211
Variational problem      207
Whitney'sum      56 165

О проекте
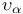