Авторизация
Поиск по указателям
Lojasiewicz S. — Introduction to Complex Analytic Geometry
Обсудите книгу на научном форуме Нашли опечатку?
Название: Introduction to Complex Analytic GeometryАвтор: Lojasiewicz S. Аннотация: The subject of this book is analytic geometry, understood as the geometry of analytic sets (or, more generally, analytic spaces), i.e. sets described locally by systems of analytic equations. Though many of the results presented are relatively modern, they are already part of the classical tool-kit of workers in analytic and algebraic geometry and in analysis, for example: the theorems of Chevalley on constructible sets, of Remmert-Stein on removable singularities, of Andreotti-Stoll on the fibres of a finite mapping, and of Andreotti-Salmon on factoriality of the Grassmannian. The chapter on the relationship between analytic and algebraic geometry is particularly illuminating. This book should be regarded as an introduction. Its aim is to familiarize the reader with a basic range of problems, using means as elementary as possible. At the same time, the author's intention is to give the reader accesss to complete proofs without the need to rely on so-called 'well-known' facts. All the necessary properties and theorems have been gathered in the first chapters – either with proofs or with references to standard and elementary textbooks.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1991Количество страниц: 523Добавлена в каталог: 09.06.2006Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Holomorphic mapping 102 Holomorphic of analytic locally analytic sets 230 204 Holomorphic of analytic manifolds 117 Holomorphic of analytic spaces 280 Holomorphic of at a point 117 Homogeneous component of degree i (of a polynomial) 15 22 Homogeneous coordinates (of a point in 357 Homogeneous coordinates, a mapping expressed in 357 Homogeneous coordinates, a set given in 357 Homogeneous mapping of degree k 14 Homogeneous polynomial 15 Homographics 437 Homological dimension 60 Homotnorphism of modules 1 Homotnorphism of rings 1 Hurwitz' theorem 447 Hyperplane at infinity 359 Ideal in a coordinate system 140 Ideal of an algebraic set 352 Ideal of an algebraic set, in R(V) 428 Ideal of an analytic germ 101 Ideal of an analytic germ in the ring of an analytic germ 225 Image of a germ under a germ of a homeomorphism 82 Image of a germ under a homeomorphism 80 Immediate ideal (to an ideal) 53 Immersion 122 Immersion at a point 122 Implicit function theorem 108 122 Indetermination point of a meromorphic function 440 Induced homo- (mono-, epi-, iso-) morphism of rings of polynomials 16 Induced structure of a manifold on a submanifold 110 Integral closure of a ring in a ring 31 Integral element over a ring 29 Integral ring over a ring 31 Integrally closed ring 31 Integrally closed ring in a ring 31 Invariant with respect to a group of automorphisms a subset 178 Invariant with respect to a group of automorphisms, a mapping 178 Irreducible (simple) algebraic set 354 470 Irreducible (simple) analytic germ 163 283 Irreducible (simple) analytic set 215 Irreducible (simple) locally analytic set 215 279 Irreducible element 7 Isolated ideals (for an ideal) 35 Isolated zero of a system of homogeneous equations 432 Isomorphic (biholomorphic) analytic germs 231 Isomorphic (biholomorphic) analytic spaces 281 Isomorphic holomorphic mappings (into an analytic apace) 286 287 Isomorphic manifolds 118 Isomorphism of algebraic sets 426 Isomorphism of algebraic spaces 477 Isomorphism of Grassmann spaces 92 Isomorphism of quasi-algebraic sets 473 Jacobi matrix, complex 102 k-topographic submanifold at a point in a coordinate system a subset of 126 k-topographic submanifold at a point, a subset of 126 Krull's dimension of a (local noetherian) ring 66 Krull's height theorem 54 Krull's intersection theorem 43 Krull's principal ideal theorem 63 Krull's topology 30 Lattice in a vector spare 130 Leading coefficient of a polynomial 10 Leading coefficient of an element of Qn 142 Lie group, (complex) commutative 120 Light mapping (at a point) 266 300 Linear mapping 1 Liouville's theorem 104 Local C-ring 42 Local connected covering of 79 Local homeomorphism 77 Local homomorphism 30 Local normalization lemma 346 Local normalization of algebraic spaces, a theorem on 470 Local normalization of an algebraic eat, a theorem on 471 Local normalization theorem 346 Local property of holomorphic mappings 286 Local ring 30 Localization (of an integral domain to an ideal) 46 48 Locally analytic subset of a manifold 1&6 Locally analytic subset of an analytic space 277 Locally biholomorphic mapping 110 273 Locally bounded mapping 76 Locally bounded near a set, a function 106 Locally closed set 73 Locally finite family of subsets 72 Locally irreducible analytic space 207 Locally l-bounded near a set, a mapping (into a manifold) 163 Locally topographic submanifold 126 Locally topographic submanifold in 126 Locus of an ideal 162 283 Locus of germs 160 Locus V(f) 160 m-sequence 61 M-sequence, maximal 62 Manifold, an analytic space ia a 276 Manifold, complex, of dimension n 113 Manifold, real analytic 113 Manifold, smooth 112 Mapping in a coordinate system 20 Mather — Nakayama lemma 10 Maximal ideal 7 Maximum principle 102 118 234 236 Meromorphic fraction 438 Meromorphic function 430 Meromorphic germ of a meromorphic function 441 Minimal polynomial for an algebraic element over a Held 26 Minimal polynomial for an integral element over a factorial ring 31 Modification of an analytic space in an analytic set, (proper) 288 Module 1 Monic element of 142 Monic polynomial 10 Montel's theorem 106 Multiple factor 27 Multiple factor, characterization of its existence for monic polynomials 28—20 Multiplicity of a *-covering 301 Multiplicity of a covering 78 Multiplicity of a covering at a point 78 Multiplicity of a factor in a decomposition 27 Multiplicity of a mapping at a point 266 Multiplicity of a normal triple 203 Multiplicity of a pole (of a meromorphic function on a one-dimensional manifold) 111 Multiplicity of a quasi-cover 180 Multiplicity of an isolated zero of a system of homogeneous equations 132 Multiplicity theorem 288 Multiprojective space 358 Musili's lemma 101 N-polynomial, a holomorphic function is 128 Nakayama's lemma 40 Natural topology of a finite dimensional vector space 84 Nearly everywhere holomorphic function 438 Newton's identities 24 Nilpotents, ring without 36 Normal analytic space 332 Normal analytic space at a point 337 Normal point of an analytic space 337 Normal representative of an analytic germ 206 Normal triple 203 Normal triple of an analytic germ 203 Normalization 343 Normed affine space 114 Nostherian ring 31 Oka — Abhyankar theorem 341 Oka's coherence theorem 320 326 Oka's theorem about universal denominators 333 One-sheeted covering 78 Open mapping 71 P-algebraic Mt 386 Parameters, system of 56 Ploski — Winiarski proposition 300 Pluecker's coordinates 300 Pluecker's coordinates dual 370 Pluecker's embedding 300 308 Pole of a meromorphic function 440 Polynomial function 17 Polynomial mapping of affine spaces 22 Polynomial mapping ofvector spaces 20 Polynomial on a vector spare 20 Preparation theorem in Thom — Martinet version 148 Primary ideal 34 Primary irreducible representation 31 Prime element 7 Prime ideal 6 Primitive element for a *-covering 308 Primitive element of an extension of a field 20 Primitive element of an extension of a ring 33 Primitive element theorem for fields 29 Primitive element theorem for rings 33 Primitive polynomial 27 Principal algebraic subset of a projective space 112 Principal algebraic subset of an affine space 351 Principal analytic germ 184 100 Principal ideal 4 Principal quasi-algebraic set 463 Principal set (globally analytic) 154 Projective closure (compactification) of a vector space 369 Projective hyperplane 95 Projective line 96 Projective space (topology) 87—03 Projective space as a complex manifold 366 Proper ideal 6 Proper inverse image (under a blowing-up) 372 377 Proper mapping 76 Puiseux theorem (1st version) 170 Puiseux theorem (2nd version) 172 173 Quasi-algebraic subset a vector space 303 Quasi-algebraic subset of an algebraic space 476 Quasi-cover 180 Quasi-covers, the first lemma on 181 Quasi-covers, tho second lemma on 182 Quasi-transversal intersection manifolds 380 Quasi-transversal intersection of germs 380 Quotient of a (commutative complex) Lie group by a discrete subgroup 120 130 Quotient of a manifold by a group of biholomorphic mappings acting discretely 120 R-linear 06 Radical of an ideal 3 Rank of a holomorphic mapping 122 Rank of a holomorphic mapping at a point 122 Rank of a holomorphic mapping locally analytic sets 208 Rank of a holomorphic mapping of analytic spaces 282 Rank of an ideal 41 Rank thorem 134 136 138 Rational function 440 Regular ( 141 Regular (ideal or germ) in a coordinate system 186 Regular analytic germ 180 Regular function, (algebraically) 404 477 Regular germ, (algebraically) 469 Regular ideal (in the ring 180 Regular mapping, (algebraically) 420 403 477 Regular points of a quasi-algebraic set 476 Regular points of an analytic set 208 Regular points of an analytic space 278 Regular ring 06 Regular separation condition 242 243 Regularity of a ring (characterisation by means graded rings) 66 Relations, family of modules of 319 Relatively prime elements 28 Remmert — Stein theorem on removable singularities 240 Remmert's constant rank theorem 295 296 Remmert's open mapping theorem 207 Remmert's proper mapping theorem 290 312 Remmert's rank (of a holomorphic mapping of analytic spaces) 206 Removable singular point of a nearly everywhere holomorphic function 438 Residual field of a local ring 40 Resolution, finite free 60 Restriction of a germ of a function 81 Riemann lemma 106 162 Riemann sphere 128 Rigid property (of holomorphic mappings) 286 Ring 1 Ring 130 Ring 138 Ring 142 Ring of an algebraic set 426 Ring of an analytic germ 226 Ring of fractions over a ring 8 Ring of principal ideals 7 Ritt's lemma 217 Roots, theorem on continuity of 80 Rouche's lemma 201 Rudin — Sadullaev theorem 302 Rudin's theorem 301 Rueckert's clasic descriptive lemma 104 Rueckert's descriptive lemma 180 Rueckert's lemma for algebraic sets 402 Rusek — Winiarski inequality 434 Sadullaev's subspace (of an algebraic set) 388 Sadullaev's theorem 389 Sard's theorem 266 Schubert's cycle 90 Schumacher's theorem 328 Segre's embedding 368 Semicontinuity, a theorem on 267 312 Serre's algebraic graph theorem 464 477 Serre's criterion 62 342 Serre's lemma 468 480 Sheaf of meromorphic germs 440 Siegel — Thimm theorem 446 Simple (irreducible) algebraic set 364 476 Simple (irreducible) analytic germ 163 Simple (irreducible) analytic set 216 270 Simple (irreducible) locally analytic set 216 Simple components of a (locally) analytic set 217 Simple components of an analytic germ 164 Simple components of an analytic space 278 Simple root of a polynomial 20 Singular point of a nearly everywhere holomorphlc function 438 Singular points of a (quasi-) algebraic set 476 Singular points of an analytic set 208 Singular points of an analytic set space 278 Smooth analytic apace 270 Smooth constructive set 262 Smooth germ 166 Stratification, complex 240 Structure of an algebraic manifold on 482 Structure of an algebraic manifold on P(X), (natural) 481 Sublocal property (of holomorphic mappings) 286 Submanifold at a point, a set is 110 Submanifold at a point, characterization of 123 Submanifold of an analytic space 277 278 Submanifold, (complex), as a subset, as a submanifold 116 119 Submersion 137 Submersion at a point, a holomorphic mapping is 136 Subspace of an algebraic space, (algebraic) 476 Subspace, protective k-dimensional 06 Substitution of a homeomorphism into a germ of a function 83 Subtori 133 Subtori, translated 134 Symbolic powers of a prime ideal 48 61 Symmetric polynomials, theorem on 24 Symmetric with respect of a group of variables a subset 179 Symmetric with respect of a group of variables, a mapping 170 Sysygy theorem 70 Syzygies, module of 67 60 Syzygies, n-th module of 60 Tangent space, (complex) 121 Taylor's formula 101 Thin subset 152 Thin, a nowhere dense analytic set is 167
Реклама
) 
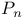is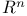 
is a homeomorphism 
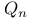
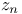-regular) germ
) 
of germs of holomorphic functions at a point a of a manifold M 
, (natural) 
|
|
О проекте