|
|
 |
| Авторизация |
|
|
|
| Поиск по указателям |
|
|
|
|
|
|
|
 |
|
|
|
| Gut A. — Stopped Random Walks: Limit Theorems and Applications |
|
|
|
| Предметный указатель |
Renewal theorem, elementary, random walk analogue 88
Renewal theorem, key 53 61
Renewal theorem, key, remainder term estimate 89
Renewal theory 2—6 8 47—62 74
Renewal theory, for Markov chains 62
Renewal theory, for oscillating random walks 6
Renewal theory, for random walks, (on the real line) 5 61 62
Renewal theory, for random walks, with positive drift 5 74—107
Renewal theory, in higher dimensions 61
Renewal theory, Markov 62
Renewal theory, multidimensional 62
Renewal theory, multivariate 62
Renewal theory, nonlinear 7 133 146 163
Renyi 3 8 15 75 85 110 122
Revuz 6
Richter 4 11 12
Robbins 23 24 42 43 93 95 106 107
Root 20
Rosen 67
Rouletts 126—127
Seal 125
Seneta 134 180
Sequential analysis 1 2 8 9 22 24
Serfozo 62 150 162 164
Siegmund 7 24 95 102 106 109 113 133 135 137 138 140 146
Skorohod 151 172 173 175 178
Slowly varying function 61 116 134 180—182
Slowly varying function, representation formula 181
smith 8 48 54 62 81 82 106 109 111 113 115
Snell 53
Solovyev 122
Sparre Andersen 4 125
Spitzer 4 6 62 65 67 88 90
Sreehari 181
Stable law 16 36 150—151
Stable law, domain of attraction of 6 16 57 60 61 86 115 131 138 151 153 157 159 161 173
Stable process 151 153 173
Stable process without negative jumps 157 159
Stable process without positive jumps 153 157 161
Stam 62
Steinebach 85
Stone 6 89
Stopped random walk 4—6 8—45 51 75 76 78 83 91—93 148 162 167 170
Stopped random walk, central limit theorem 15—16 38 111—112
Stopped random walk, complete convergence 42—43 104
Stopped random walk, convergence rate 42—44 104
Stopped random walk, law of large numbers 13—14 37 93 109—111 135
Stopped random walk, law of the iterated logarithm 42 102 117 162 163
Stopped random walk, moments 20—28 51 78 133
Stopped random walk, moments, convergence 36—39 93 109—114 144 167
Stopped random walk, uniform integrability 28—36 91—95 111 138
| Stopped random walk, weak convergence 148—151 157
Stopped sum see “Stopped random walk”
Stopped two-dimensional random walk 108 109—118 157—159 163
Stopped two-dimensional random walk, applications 118—132
Stopping summand 39—41 79 83 84 91 93 135 138 144
Stopping time 4 5 7 9 17 20 28 37 39 46 50 60 68 74 76—78 133 170 178
Storage and inventory theory 1 2
Stout 7 41 177
Strassen 7 41 147 161 162 177—178
Strong approximation 163 177—178
Sums of random variables, dependent 107 146
Sums of random variables, independent 106 146 167—169 178
Sums of random variables, m-dependent 78 101
Sums of random variables, non-i.i.d. 106—107 146
Sums of random variables, stationary 101 107
Sums of random variables, vector valued 117
Szynal 43
Tacklind 57 97
Takacs 8 54 122
Teicher 6 7 23 138
Teugels 57 61
Thorisson 53
Tightness 151 172 179
Topology, 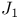 154 156—157 172—173 179
Topology,  155 172—173
Topology, , graph 173
Topology, , parametric representation 156 173
Topology, U 157 171 173 179
Torrang 42
Tweedie 53
Uniform continuity in probability 15 (see also “Anscombe condition”)
Uniform integrability 4 9 17 18 28—36 40—41 56—57 90—92 98 109—112 130 138—143 145 165—167 178 in “Convergence moment”)
Vervaat 152 156 163 164 175 178
von Bahr 109 125
Wainger 62 89 107
Wald 73
Weak convergence 147—161 171—176
Weak convergence in the 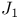-topology 148 150—160 173—176
Weak convergence in the -topology 153—156 159
Weak convergence in the U-topology 172 174 176
Whitt 151 155—157 164 175
Wiener — Hopf factorization 4 46
Wiener, measure 148 150 172
Wiener, process 147 158
Williamson 53 61 106
Wintner 41 177—178
Wolfowitz 90 132
Woodroofe 7 97 98 100 102 133
Yahav 62
Yu 33
Zygmund 19 20 167 169
|
|
|
| Реклама |
|
|
|
|
|
О проекте