|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Greub W., Halperin S., Vanstone R. — Connections, curvature, and cohomology. Volume 1 |
|
|
 |
| Предметный указатель |
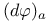 88 88
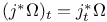 , , 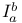 156 156
 120 120
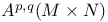 , , 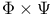 122 122
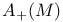 , , 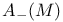 122 122
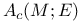 , , 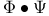 152 152
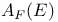 , , 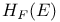 295 295
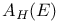 , , 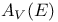 283 283
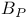 177 177
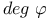 240 240
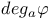 260 260
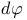 95 95
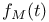 , , 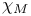 178 178
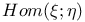 50 50
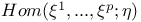 , , 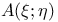 51 51
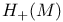 , , 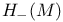 187 187
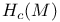 , , 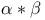 189 189
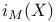 110 110
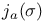 330 330
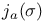 , , 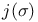 369 369
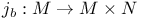 97 97
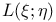 , ,  56 56
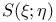 , , 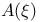 51 51
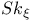 72 72
 22 22
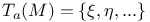 87 87
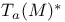 , , 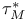 97 97
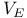 281 281
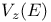 280 280
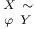 109 109
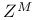 , ,  111 111
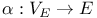 , , 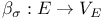 291 291
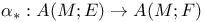 151 151
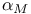 , , 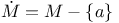 252 252
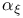 360 360
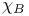 , D 320 , D 320
 145 145
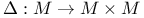 29 29
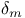 148 148
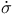 , , 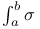 , , 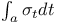 153 153
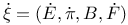 105 105
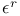 , , 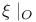 , , 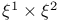 46 46
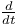 116 116
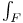 298 300 298 300
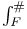 306 306
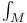 160 160
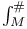 , , 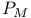 , , 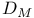 194 194
 , , 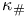 208 208
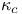 , , 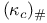 , , 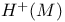 210 210
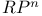 , , 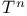 23 23
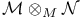 , , 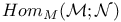 30 30
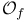 , , 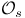 16 16
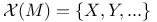 106 106
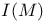 , carr f 30 , carr f 30
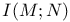 24 24
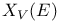 , , 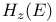 , , 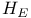 282 282
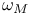 201 201
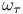 , , ![$[\tau, \sigma]$](/math_tex/ef39a8a38b928813df436f2cdd3c021f82.gif) 326 326
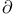 181 181
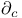 193 193
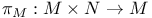 29 29
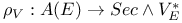 284 284
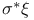 48 48
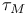 , , 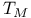 94 94
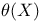 142 142
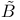 , , 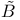 70 70
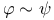 33 33
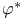 121 121
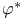 , , 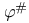 , , 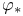 62 63 62 63
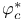 , , 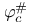 , , 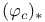 , , 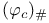 190 190
 296 296
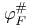 , , 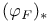 , ,  297 297
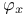 45 45
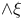 , , 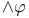 , , 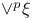 , , 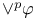 57 58 57 58
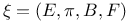 , , 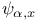 44 44
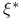 , , 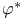 52 52
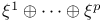 54 54
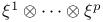 55 55
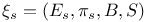 105 105
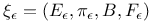 359 359
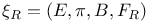 73 73
A(M; E) 150
Abstract simplicial complex 217
Adjoint, Poincare 400
Affine simplex 236 388
Affine spray 135 418
Algebra of smooth functions 30
Algebra, anticommutative 4
Algebra, cohomology 11 176
Algebra, connected 4 177
Algebra, exterior 4 57
Algebra, graded 3 4
Algebra, graded differential 11
Algebra, Lie 4 107 152 173
Algebra, symmetric 4 58
Anticommutative algebra 4
Anticommutative tensor product of graded algebras 4
Antiderivation 4 141
Associated sphere bundle 105 293
Atlas 15 414
Atlas, equivalent 22 24
Atlas, finite 20
Atlas, smooth 22
Barycentre 390
Base space 38
Basis for topology 14
Betti groups 232
Betti numbers 178 205 231
Bigraded module 8
Borsuk — Ulam theorem 275
Boundary 232
Boundary, manifold-with 139 231 350 415
Bundle of skew transformations 72
Bundle, along fibre 281
Bundle, composite 311
Bundle, cotangent 97 173
Bundle, deleted 105
Bundle, disc 381
Bundle, exterior algebra 57
Bundle, fibre 38
Bundle, isomorphism 45
Bundle, jet 132
Bundle, map 45 47 84 291
Bundle, normal 138 380
Bundle, pseudo-Riemannian 66 85
Bundle, quotient 84
Bundle, Riemannian 66
Bundle, space 38
Bundle, sphere 105
Bundle, subbundle of 44 68
Bundle, symmetric algebra 58
Bundle, tangent 94 385
Bundle, vector 44
Bundle, vertical subbundle of 281
Canonical tensor product of graded algebras 4
Canonical transformation 173
carr  , , 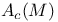 147 147
carr  59 59
Carrier of cross-section 59
Carrier of differential form 147
Carrier of smooth function 30
Carrier, compact 147 189 295 380
Cauchy's integral theorem 235
Cayley map 25
Cayley numbers 132 175
Cech cohomology 238
Chain 232
Chain, degenerate 236
Chain, invisible 236
Charts 15
| Charts, identification map of 22
Classifying map 86
Closed differential form 176
Coboundary 9 176
Cochain 218 348
Cocycle 9 176
Cohomology of  with compact supports 190 with compact supports 190
Cohomology of real projective spaces 187
Cohomology of sphere bundles 316ff. 344
Cohomology of spheres 185
Cohomology of vector bundles 352ff.
Cohomology with compact supports 189
Cohomology, algebra 11
Cohomology, algebra of compact manifolds 218
Cohomology, algebra of manifolds 176
Cohomology, algebra of nerve 218
Cohomology, axioms 178 190
Cohomology, space 9
Coincidence point 405 409 416
Coincidence, numbers 400ff.
Compact Kuenneth homomorphism 210
Compact manifolds 41 203 205 218 228
Compact supports 141 189 295 380
Complex functions 274
Complex projective space 42 415
Complex structure 73
Complex vector bundle 73 86
Complexification of vector space 2 27
Composite bundle 311
Composition map 57
Conjugate parallelism 175
Connected algebra 4 177
Connected manifold 177
Connected sum of manifolds 140
Connecting homomorphism 10 181 193
Constant map 24
Constant rank 84
Continuous homotopy 41
Continuous local degree 387
Continuous vector field 389
Contractible manifold 86 183
Contracting homotopy 183
Contraction 183
Contravariant tensor field 119
Coordinate functions 131
Coordinate representation for fibre bundles 38 40
Coordinate representation for vector bundles 44 45 70
Coordinate representation, Riemannian 68
Coordinate transformation 44
Cotangent bundle 97 173
Cotangent space 96
Cotangent vector 96
Covariant tensor field 118
Cover(ing), open 14
Covering transformation 71
Critical point 136 416
Critical point, nondegenerate 138
Critical value 136 245
Cross-section(s) of exterior power 81
Cross-section(s) of fibre bundle 38
Cross-section(s) of sphere bundle 337
Cross-section(s) of tangent bundle 106
Cross-section(s) of tensor product 80
Cross-section(s), index of 330 367
Cross-section(s), Lie algebra of 107
Cross-section(s), mappings of 62
Cross-section(s), module of 60 78
Cross-section(s), normed 66
Cross-section(s), pull-back of 325
Cross-section(s), smooth family of 153
CYCLE 232
Cycle, fundamental 237
Dashed degree 385 386
De Rham cohomology algebra 176
De Rham existence theorem 233
De Rham isomorphism 218 228
de Rham theorem 218ff.
Definite integral of smooth family 153
Deformation retract 184
Degenerate chain 236
Degree, (mod 2) 274
Degree, global 240 264 408 414
Degree, global dashed 386
Degree, local 259 260 264 382 383 387
Degree, local dashed 385
Degree, mapping 240ff.
Deleted bundle 105
density 171 233
Derivations as tangent vector fields 106
Derivations in algebra 2
Derivations, Lie product of 107
Derivative of map 12 88ff. 95
Derivative of smooth family 153
Derivative, exterior 145
Derivative, Lie 142
Determinant function in real vector space 1 124
Determinant function in vector bundle 64 70
Diagonal map 29
Diffeomorphism 12 24 35ff.
Diffeomorphism, local 99
Difference class 325
Differentiable map 12
Differential algebra 9
Differential equations 13 112ff.
Differential forms 115 119ff. 283ff.
Differential forms, closed 176
Differential forms, cochain of 218 348
Differential forms, components of 131
Differential forms, exact 176
Differential forms, exterior derivative of 145
Differential forms, harmonic 231
Differential forms, horizontal 283
Differential forms, invariant 144 158
Differential forms, invariant, with noncompact carrier 164
Differential forms, smooth family of 153
Differential forms, vector valued 149 163
Differential operator 9
Differential operator of order p 133 134
Differential space 9
dim M 15 17
Dimension theory 17ff. 239
Direct limit 238
Directed system of vector spaces 238
Disc bundles 381
Disjoint union axiom 179 232
distribution 134
Divergence 171 234
Double cover 71 123 399
Double of manifold 140
Dual of module 7
Dual of strong bundle map 52
Dual vector bundles 52 67 80
Ehresmann connection 314
Eigenvalue, eigenvector 85
Embedded manifold 102
Endomorphism of vector bundle 85
Euclidean half-space 139
Euclidean space 2
Euclidean space, maps between 260
Euclidean space, one-point compactification of 23 25
Euler class 320 328 334 391
Euler class of Whitney sum 345
Euler class, index sum and 372
Euler class, relative 349
Euler class, Thom class and 364
Euler — Poincare characteristic 178 186 205ff. 228 391 408 414 416
Euler — Poincare formula 11
Evaluation map 56
Exact differential form 176
Exact sequence 8 84
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



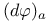
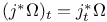 ,
, 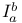

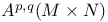 ,
, 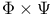
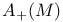 ,
, 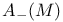
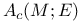 ,
, 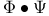
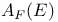 ,
, 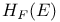
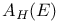 ,
, 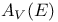
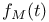 ,
, 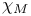
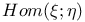
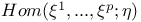 ,
, 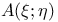
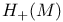 ,
, 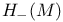
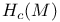 ,
, 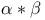
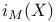
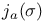
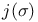
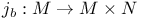
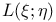 ,
, 
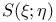 ,
, 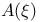
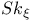

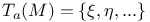
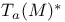 ,
, 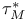
 ,
, 
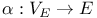 ,
, 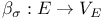
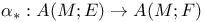
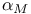 ,
, 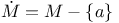
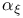
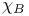 , D
, D 
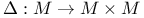
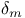
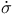 ,
, 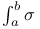 ,
, 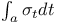
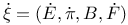
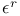 ,
, 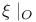 ,
, 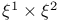
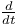
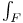
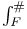
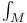
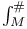 ,
, 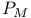 ,
, 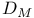
 ,
, 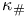
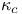 ,
, 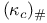 ,
, 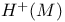
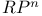 ,
, 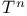
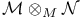 ,
, 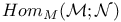
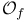 ,
, 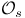
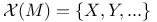
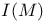 , carr f
, carr f 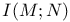
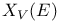 ,
, 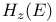 ,
, 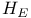
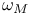
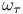 ,
, ![$[\tau, \sigma]$](/math_tex/ef39a8a38b928813df436f2cdd3c021f82.gif)
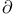
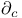
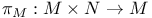
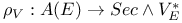
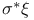
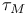 ,
, 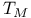
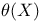
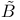 ,
, 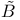
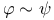
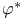
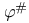 ,
, 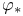
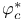 ,
, 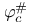 ,
, 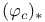 ,
, 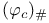

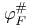 ,
, 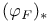 ,
, 
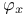
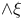 ,
, 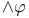 ,
, 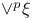 ,
, 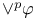
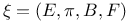 ,
, 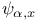
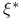 ,
, 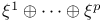
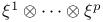
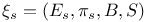
 ,
, 

 with compact supports
with compact supports