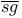Авторизация
Поиск по указателям
Elliott Mendelson — Introduction to mathematical logic
Обсудите книгу на научном форуме Нашли опечатку?
Название: Introduction to mathematical logicАвтор: Elliott Mendelson Аннотация: The Fourth Edition of this long-established text retains all the key features of the previous editions, covering the basic topics of a solid first course in mathematical logic. This edition includes an extensive appendix on second-order logic, a section on set theory with urlements, and a section on the logic that results when we allow models with empty domains. The text contains numerous exercises and an appendix furnishes answers to many of them.Introduction to Mathematical Logic includes:opropositional logicofirst-order logicofirst-order number theory and the incompleteness and undecidability theorems of G?del, Rosser, Church, and Tarskioaxiomatic set theoryotheory of computabilityThe study of mathematical logic, axiomatic set theory, and computability theory provides an understanding of the fundamental assumptions and proof techniques that form basis of mathematics. Logic and computability theory have also become indispensable tools in theoretical computer science, including artificial intelligence. Introduction to Mathematical Logic covers these topics in a clear, reader-friendly style that will be valued by anyone working in computer science as well as lecturers and researchers in mathematics, philosophy, and related fields.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: 2-nd editionГод издания: 1979Количество страниц: 336Добавлена в каталог: 08.12.2013Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Partial function 7 Partial order 9 61 183 Partial recursive 227 Partial, permutation 263 Partial, potentially 263 Partial, relation 142 Partially Markov-computable 227 Particularization rule A4 73 Peano's postulates 121 122 134 Peter, R. 260 pf 169 Polish notation 19 Polyadic algebras 103 Possible definitions 171 Post, E.L. 239 256 264 265 Potentially recursive 263 Power class 179 Power of the continuum 8 Power set 181 Power set, axiom 181 PP 169 PR-formula 164 Precisely k-valid 72 Predecessor 260 Predicate, calculus 60 Predicate, letter 46 Predicate, pure monadic, calculus 170 Predicate, pure, calculus 90 169 Predicative wf 178 Premiss 30 Prenex normal form 88—92 Presburger, M. 134 266 Prime number 142 143 Prime power factorization 143 Primitive connectives 31 Primitive recursive function 138 Primitive recursive relation 142 Principal, connective 15 Principal, filter 108 Principal, letter 249 Principle of complete induction 8 9 131 Principle of dependent choice 214 Principle of Mathematical Induction 8 121 122 Principle, least-number 131 Principle, normalization 238 Principle, well-ordering 9 210 Product, cartesian 5 110 179 Production (simple, terminal) 222 Productive 264 Projection 228 Projection functions 135 proof 30 32 Proof, by contradiction 74 Proof, of an equation 249 Propagation 228 Proper axiom 59—60 Proper class 174 Proper ideal 10 Proper inclusion 173 Proper subset 5 Property 6 174 Proposition 31 32 Propositional calculus 12—44 Propositional calculus, intuitionistic 42 Propositional connective 11 13 PS 169 Pure first-order predicate calculus (PP) 90 169 Pure monadic predicate calculus 170 Putnam, H. 221 264 Quantifiers 45 Quantifiers, bounded 142 Quasi-quotation 31 (f.n.) Quine, W.V. 4 13 219 Quotation marks 13 (f.n.) Quotient (qt) 133 140 r.e. see "Recursively enumerable" Rabin, M. 167 Ramification 231 RANGE 6 180 Rank 214 Rasiowa, H. 67 (f.n.) 70 100 101 RE-formula 164 Recursion 138 Recursion, course-of-values 146 Recursive algorithm 236 Recursive function 138 Recursively (essentially) undecidable 166 Recursively axiomatizable 162 Recursively enumerable 260 Recursively equivalent 264 Reduced direct product 112 Reflexive 6 Reflexive partial order 9 Reflexive total order 9 Regular ordinal 205 Regularity, axiom of 213 Relation, arithmetical 151 Relation, binary 6 179 Relation, connected 183 Relation, equivalence 6 Relation, expressible 134 Relation, identity 6 180 Relation, irreflexive 183 Relation, membership 173 185 Relation, n-place 6 Relation, primitive recursive 142 Relation, recursive 142 Relation, reflexive 6 Relation, representing 137 Relation, symmetric 6 Relation, transitive 6 183 Relation, weakly expressible 262 Relative complement 5 Relatively interpretable 172 Relativization 172 Remainder (rm) 133 140 Replacement axiom 182 Replacement Theorem 75 Representable function 135 Representing relation 137 Rescher, N. 40 Restriction of a function 7 181 Richard's paradox 3 Rings, elementary theory of 82 Robinson's System 167 Robinson, A. 98 99 115 119 Robinson, J. 221 Robinson, R.M. 4 167 168 171 172 173 260 Rogers, H., Jr. 258 264 266 Rosenbloom, P. 103 Rosser, Goedel-, Theorem 160 162 Rosser, J.B. 4 40 41 78 88 160 217 219 RR 167 Rubin, J. 219 Rule A4 73 Rule C 76—78 Rule E4 73 Rules of Inference 30 249 Russell's paradox 2 4 183 Russell, B. 3 4 Ryll-Nardzewski, C. 167 S (first-order arithmetic) 121—122 S (first-order arithmetic), consistency of 126 163 S (first-order arithmetic), Goedel's Theorem for 159 Satisfaction relation 51—52 54 Satisfiable 56 Schema, algorithm 222 Schema, axiom 31 Scholz, H. 59 (f.n.) 172 Schroder-Bernstein Theorem 2 194 Schuette, K. 164 Scope 47 Second 100 Section 185 Segment 185 Semantical 59 (f.n.) 70 Sentence 50 Sentence, atomic 15 Sequence (denumerable, finite) 8 Set 2 5 174 Set, Dedekind-finite 198 Set, denumerable 8 198 Set, empty (null) 5 175 Set, finite 197 Set, infinite 8 198 Set, power 181 Set, sum 180 Set, unit 5 Sets, disjoint 5 Sg, 122 Shannon, C. 21 Shepherdson, J. 216 218 Shoenfield, J. 217 219 Sierpinski, W. 95 (f.n.) 208 209 217 Sikorski, R. 10 67 70 101 102 Similar ordered structures 184 Similar wfs 65 Similarity mapping 184 Simple production 222 Simple set 263 Simply transforms 223 Singular ordinal 218 Skolem normal form 90 Skolem — Loewenheim Theorem 71 84 Skolem — Loewenheim Theorem, Downward 108 Skolem — Loewenheim Theorem, Upward 107 Skolem — Loewenheim, Theorem 71 84 Skolem's paradox 196 Skolem, T. 219 Smullyan, R. 152 264 Sonner, J. 216 Specker, E. 217 219 Standard model 126 Standard part 117 State, internal 240 241 Statement form 13 Statement letter 13 31 Stone, M. 101 Strongly inaccessible ordinal 218 Strongly representable function 135 Stroyan, K.D. 119 Submodel 104 Subset 5 Subset, proper 5 Subsets, axiom of 181 Substitution 138 Substructure 104 Successor 121 Successor function 135 Successor ordinal 188 Sufficiently strong theory 172 Suitable 39 Sum class 179 Sum of cardinals 196 Sum set 180 Suppes, P. 219 Suranyi, J. 266 Symbol 29 symbols 240 symmetric 6 Syntactical 59 (f.n.) 70 System of equations 249 Szmielew, W. 98 267 Table, truth 11 Takeuti, G. 217 Tape 240 Tape, instantaneous, description 241 Tarski — Vaught theorem 106 Tarski's theorem 166 Tarski, A. 39 42 59 98 103 106 107 108 168 171 172 212 216 267 Tautology 16 Teichmueller — Tukey Lemma 211 Term 46 249 Term, closed 68 Terminal production 222 Terminally transforms 223 Theorem 30 Theory of equality 81 Theory, axiomatic 29 Theory, complete 66 Theory, first-order 59—60 61 Theory, formal 17 29 Theory, generalized first-order 95 Theory, recursively axiomatizable 162 Theory, recursively undecidable 166 Theory, sufficiently strong 172 Theory, type 4 219 Theory, with equality 79 83 Thompson, F.B. 103 Total function 7 Total order 9 183 184 Transfinite induction 9 187 189 Transitive class 185 Transitive closure 213 Transitive relation 6 183 Translation 239 Trichotomy 210 True wf 52 True, logically 17 57 Truth function 14 16 Truth table 11—15 Truth table, abbreviated 15 Truth values 11 Truth-functional combination 11 Turing algorithms 241 Turing machine 240—242 Turing, A.M. 239 240 Turing-computable 242 Turquette, A.R. 40 Tychonoff's theorem 99 Types, theory of 4 219 Ulam, S. 216 Ultra-filter 109 Ultrafilter 109 Ultrafilter, theorem 110 Ultrapower 112 Ultraproduct 112 Undecidable problems 265—266 Undecidable sentence 159 Undecidable theory 30 Undecidable, recursively 166 Uniformly continuous 119 union 5 177 Unit set 5 Universal algorithm 238 Universal choice function 212 UNIVERSAL class 177 Universal quantifiers 45 Univocal 181 Unordered pair 5 175 Unrestricted mu-operator 227 Upward Loewenheim — Skolem — Tarski Theorem 107 Upward Skolem — Loewenheim, Loewenheim — Tarski Theorem 107 Valid, logically 56 Van der Waerden, B. 98 Variable, free (bound) 48 Variable, individual 46 Vaughn, H. 100 Vaught, R. 96 106 108 216 218 von Neumann, J. 4 173 214
Реклама
 |
|
О проекте
|
|
О проекте



 -Theorem
-Theorem