|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| von Collani E., Drager K. — Binomial Distribution Handbook for Scientists and Engineers |
|
|
 |
| Предметный указатель |
 -exclusion space 126 -exclusion space 126
 -estimator 105 106 -estimator 105 106
 -measurement & prediction space for -measurement & prediction space for  72 78 72 78
 -measurement h prediction space 70 -measurement h prediction space 70
 -measurement interval 71 73 -measurement interval 71 73
 -measurement procedure 72 73 -measurement procedure 72 73
 -measurement procedure, complete 105 -measurement procedure, complete 105
 -measurement procedure, Neyman 79 -measurement procedure, Neyman 79
 -measurement procedure, Neyman -measurement procedure, Neyman  80 80
 -prediction procedure 73 -prediction procedure 73
 -prediction region 73 -prediction region 73
Acceptance region 9
alternative 146
Alternative hypothesis 145
Ars Conjectandi 3
Bayes approach 34 177
Bernoulli experimen 13
Bernoulli experiment 42 194
Bernoulli, Jakob 3
Binomial model 193
Binomial test 213
Chapman test 225
Clopper — Pearson confidence intervals 95
Comparison procedure 145
Comparison procedure, 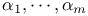 - 150 151 - 150 151
Comparison procedure, Neyman  155 155
Comparison space, 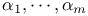 - 150 - 150
Conditional density of p 65
Conditional distribution of  64 64
Conditional mean squared error 106
Conditional measure of 6 65
Conditional test 223
Confidence interval 8 32 41
Confidence level 9 41 62
Consistency 40 100
Continuity correction 27
Convex hull 159
DATA 17
Difference of two probabilities 200
Distribution function 6 16
Distribution parameter xvi
Distribution,  24 24
Distribution, Bernoulli 19
Distribution, binomial 19 21
Distribution, F- 22 52
Distribution, hypergeometric 21 27 28
Distribution, joint 20
Distribution, Poisson 24
Distribution, standardized normal 25
Error of Type I 150
Error of Type m 150
Error of Type*II 150
Error probability 147
Essai philosophique sur les probabilites 4
Estimation theory 120
Estimator, interval 36 39
Estimator, point 36 39
Exclusion error 124
Exclusion procedure 120
Exclusion procedure Neyman 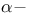 129 129
Exclusion procedure, 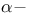 124 124
Failure probability 127 151
False decision 124
Fisher, R.A. 8
General space 37 61
Hypergeometric model 193
Inverse problem 22
Joint distribution of  64 64
Joint measure of  66 66
Kolmogorov, A.N. 5
Laplace, Pierre Simon de 25
Laplace, Simon 4
Lebesgue measure 29
Likelihood ratio 130
Likelihood ration order 131
Local 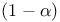 -prediction region 126 -prediction region 126
Local 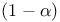 -prediction space 126 -prediction space 126
| Marginal density of p 63
Marginal probability measure  65 65
Maximum likelihood ration 154
Maximum parameter space 121
Measurable space 61
Measurement &; prediction space ![$([p, \vec{p}] \times \{0, 1, \cdots, n\})$](/math_tex/e3dd34ca1be6db6852cfaf7993b0589982.gif) 67 67
Measurement error 97
Measurement h prediction space 61 63
Measurement interval 40 98
Measurement precision 4 61 97 98
Measurement procedure 4 41 69
Measurement procedure, approximate 52
Measurement procedure, complete 98
Measurement procedure, traditional 49
Measurement range 11 29
Measurement region 97
Measurement reliability 4 40 46 97
Measurement space 60 61
Measurement space conform 102
Measurement space conformity 102
Median 219
Midpoint  -estimator 112 -estimator 112
Minimum MSE- -estimator 107 -estimator 107
Minimum variance 40
Moivre, Abraham de 25
Neyman 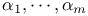 -comparison procedure 152 -comparison procedure 152
Neyman, Jerzy 5
Nonconformance probability 102
Null hypothesis 120
Null hypothesis, simple 121
Point estimate 98
Point estimator 98
Poisson distribution 203
Poisson, Simeon-Denis 24
Population 14 18
PRECISION 30
Prediction procedure 62 69 71
Prediction region 71
Prior distribution 177
probability 12
Probability space 17
Probability volume 77 106
Proportion 14
Quality characteristic 75
Quality indicator 105 129
Quantile 22
Random experiment 14
Random phenomenon 13
Random sample xvi 7 19 35
Random sample, classification 16
Random sample, independent 16
Random variable xvi
Real-valued model 18
Real-world model 18
Relative frequency 46 47 99
Reliability 10
Reliability excess 78 127 186
Reliability requirement 126
Robust estimator 101
Set, connected 70 72
Sign test 218
Significance level 122
Significance test 120
Statistical thinking 119
Success probability 127 147
Test theory 120
Test, binomial 213
Test, Chapman 225
Test, McNemar 222
Test, sign 218
Theorem, central limit 25
Theorem, Moivre — Laplace integral limit 25
Theorem, Moivre — Laplace limit 25
Theory of estimation 32
Unbiasedness 40 100
Weight function 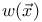 65 65
Weighted volume 76
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -exclusion space
-exclusion space  -estimator
-estimator 

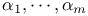 -
- 


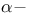

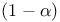 -prediction region
-prediction region 
![$([p, \vec{p}] \times \{0, 1, \cdots, n\})$](/math_tex/e3dd34ca1be6db6852cfaf7993b0589982.gif)