|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Chavel I. — Eigenvalues in Riemannian geometry |
|
|
 |
| Предметный указатель |
Associated Legendre equation and function 309
Berger isoembolic inequality 120
Berger — Kazdan inequality 114
Bochner — Lichnerowicz formula 83
Cheeger inequality, lowest Dirichlet eigenvalue 95
Cheeger inequality, lowest nonzero eigenvalue, closed problem 109
Cheeger inequality, lowest nonzero Neumann eigenvalue 259
Co-area formula 86
Comparison theorem, Bishop 68 71
Comparison theorem, Bonnet — Myers 73
Comparison theorem, Cheeger — Yau 194
Comparison theorem, Cheng 70 74
Comparison theorem, Debiard — Gaveau — Mazet 194
Comparison theorem, H. E. Rauch 67 74
Comparison theorem, Hadamard — Cartan 68
Comparison theorem, McKean 70
Comparison theorem, Morse — Schonberg 68
Comparison theorem, Obata 82
Comparison theorem, Toponogov 83
Conjugate point 62
Constant, Cheeger 95 109
Constant, isoperimetric 96 110
Constant, Sobolev 96 110
Convergence of heat flow to steady state, compact manifold 141
Convergence of heat flow to steady state, Dirichlet boundary data 170—172
Convergence of heat flow to steady state, Euclidean upper half-space 325—329
Convergence of heat flow to steady state, forms 339
Coordinates, Fermi, based on submanifold 319
Coordinates, Fermi, surface 247
Coordinates, geodesic spherical 65ff.
Coordinates, Riemann normal 317
Coordinates, sphere 37
Coordinates, spherical, Euclidean space 34
Coordinates, spherical, hyperbolic space 37
Cut locus 64
Cut point 64
Differential forms, Cheeger’s inequality and 342
Differential forms, deRham complex 334
Differential forms, eigenforms 339
Differential forms, eigenvalue estimates 342
Differential forms, Gauss — Bonnet theorem and heat equation 340—341
Differential forms, heat kernel 338
Differential forms, Hodge decomposition 335
Differential forms, Laplacian on 335
Dirichlet integral 14
Divergence theorem 6 7
Duhamel’s principle 137 145 165
Eigenfunction, 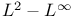 estimates 102 112 estimates 102 112
Eigenvalues, 1-dimensional problems 10
Eigenvalues, closed problem 7
Eigenvalues, closed problem, bounds, lower 112 133 251 332
Eigenvalues, closed problem, bounds, upper 77 332
Eigenvalues, closed problem, bounds, upper, L bell surfaces 251 bell surfaces 251
Eigenvalues, closed problem, calculation, projective space 36
Eigenvalues, closed problem, calculation, sphere 33
Eigenvalues, closed problem, calculation, torus 28
Eigenvalues, closed problem, lower, relation to short geodesics, Riemann surfaces 254—262
Eigenvalues, closed problem, lowest nonzero, bounds, lower 82 109 127 314 324 332
Eigenvalues, closed problem, lowest nonzero, bounds, upper, surface 94
Eigenvalues, closed problem, lowest nonzero, pinching theorem 92
Eigenvalues, closed problem, small, Riemann surface 247 300—302
Eigenvalues, Dirichlet problem 8
Eigenvalues, Dirichlet problem, bounds, lower 95 107 330
Eigenvalues, Dirichlet problem, calculation, disk, in space form 40—42
Eigenvalues, Dirichlet problem, calculation, domain, crystallographic group 33
Eigenvalues, Dirichlet problem, calculation, equilateral triangle 33
Eigenvalues, Dirichlet problem, lowest, bounds, lower 70 79 82 87 95 129
Eigenvalues, Dirichlet problem, lowest, bounds, lower, hyperbolic space 46
Eigenvalues, Dirichlet problem, lowest, bounds, upper 74 79 129
Eigenvalues, Dirichlet problem, lowest, bounds, upper, disk, hyperbolic space 80—82
Eigenvalues, Dirichlet problem, lowest, bounds, upper, L bell bell  -piece 249 -piece 249
Eigenvalues, Dirichlet problem, lowest, disk, space form 42—45
Eigenvalues, Dirichlet problem, lowest, disk, space form, Euclidean space 45
Eigenvalues, Dirichlet problem, lowest, disk, space form, hyperbolic space 46
Eigenvalues, Dirichlet problem, lowest, disk, space form, sphere 50—54
Eigenvalues, domain monotonicity, vanishing Dirichlet data 17
Eigenvalues, domain monotonicity, vanishing Neumann data 18
Eigenvalues, lower bounds from upper bounds on heat kernel 157
Eigenvalues, max-min characterization 17
Eigenvalues, minimal immersions and 312—314
Eigenvalues, mixed eigenvalue problem 8
Eigenvalues, multiplicity of 24 35 104
Eigenvalues, Neumann problem 8
Eigenvalues, Neumann problem, calculation, disks in space form 40—42
Eigenvalues, Neumann problem, lowest nonzero, bounds, lower 251
Eigenvalues, Neumann problem, lowest nonzero, bounds, upper 94
Eigenvalues, Neumann problem, lowest nonzero, disks in space form 42—45
Eigenvalues, Neumann problem, lowest nonzero, disks in space form, Euclidean space 45
Eigenvalues, Neumann problem, lowest nonzero, disks in space form, hyperbolic space 46
Eigenvalues, Neumann problem, lowest nonzero, disks in space form, spheres 50
Eigenvalues, Rayleigh’s characterization 16
Eigenvalues, Sturm — Liouville decomposition, closed eigenvalue problem 139
Eigenvalues, Sturm — Liouville decomposition, Dirichlet eigenvalue problem 169
Eigenvalues, topological perturbations with negligible effect on 207—235
Fourier transform 304ff.
Fourier transform, Fourier inversion formula 305
Fourier transform, heat equation 307
Fourier transform, Plancherel formula 305
Fourier transform, Poisson summation formula 306
Fourier transform, Weyl asymptotic formula, torus 307
Function, admissible for eigenvalue problems 15
Function, directional derivative of 1
Function, gradient of 2
Function, Hessian of 82
Function, Laplacian of 3
Function, Sobolev space of 14
Function, weak derivative of 14
Fundamental solution, heat equation see Heat kernel
Gamma function 303
Green’s formulas 6 7 165
Green’s function 173
Green’s function, Dirichlet problem 175
Green’s function, forms 339
Green’s function, relation to heat kernel 177
Heat equation, homogeneous 134
Heat equation, inhomogeneous 135
Heat equation, separation of variables 12
Heat kernel, almost Euclidean 159
| Heat kernel, Brownian motion associated to 210ff.
Heat kernel, compact manifold, bounds, lower 333
Heat kernel, compact manifold, bounds, upper 112 133
Heat kernel, compact manifold, existence 151—154
Heat kernel, compact manifold, uniqueness 138
Heat kernel, comparison theorems 192—196
Heat kernel, Dirichlet 158
Heat kernel, Dirichlet, bounds, lower 195
Heat kernel, Dirichlet, bounds, upper 108 195 331—332
Heat kernel, Dirichlet, existence 164
Heat kernel, Dirichlet, uniqueness 167
Heat kernel, Euclidean space 142—148 307—308
Heat kernel, Fourier transform and 306—308
Heat kernel, noncompact manifolds (see also Heat kernel Euclidean
Heat kernel, noncompact manifolds, bounds, lower 196
Heat kernel, noncompact manifolds, bounds, upper 180 196—206
Heat kernel, noncompact manifolds, Euclidean upper half-space 326
Heat kernel, noncompact manifolds, existence 188
Heat kernel, noncompact manifolds, space form 150 151
Heat kernel, noncompact manifolds, space form, hyperbolic plane 242—246
Heat kernel, topological perturbations with negligible effect on 207—235
Hyperbolic plane, geometry 239—241
Hyperbolic plane, heat kernel 242—246
Hyperbolic plane, upper half-plane model 262—264
Hyperbolic space, disk model 37
Hyperbolic space, geometry 266—271
Hyperbolic space, upper half-space model 264—265
Injectivity radius 118 120 247
Isoperimetric inequality, geometric 85 89 90 92 313
Isoperimetric inequality, geometric, L vy — Gromov 91 322—325 vy — Gromov 91 322—325
Isoperimetric inequality, physical, closed eigenvalue problem, surfaces 94
Isoperimetric inequality, physical, Faber — Krahn 87
Isoperimetric inequality, physical, Faber — Krahn, minimal surfaces and 93
Isoperimetric inequality, physical, Faber — Krahn, variation of 91 93
Isoperimetric inequality, physical, Neumann eigenvalue problem 94
Jump relation 159 161
Kinematic measure 117
Kinematic measure, Liouville’s theorem 117
Kinematic measure, Santalo’s formula 125 130
Manifold, connection on 2
Manifold, connection on, Christoffel symbols of 4
Manifold, connection on, curvature, operator along geodesic 63
Manifold, connection on, curvature, tensor 59
Manifold, connection on, exponential map 57
Manifold, connection on, geodesic 57
Manifold, connection on, geodesic completeness 57
Manifold, Riemannian metric 2
Manifold, tangent bundle of 1
Manifold, tangent space to 1
Mathematics of crushed ice 233—238
Maximum principle, heat operator 139 166 169 180 182
Maximum principle, Laplace operator 20 127 329—330
Metaphysical principle 77
Minimal immersions and eigenvalues 312—314
Nodal domains 19
Nodal domains, Courant’s theorem 19 92
Nodal domains, Pleijel’s theorem 24 92
Nodal sets 19
Nodal sets, convexity of 24
Nodal sets, regularity of 23
Polya conjecture 33 330 333
Ricatti equation 72
Riemannian covering, deck transformation group 27
Riemannian manifold, curvature, Gauss 60
Riemannian manifold, curvature, Ricci 60
Riemannian manifold, curvature, scalar 60
Riemannian manifold, curvature, sectional 59
Riemannian manifold, distance between points of 39
Riemannian manifold, Gauss’s lemma 59
Riemannian manifold, L vi — Civita connection on 2 vi — Civita connection on 2
Riemannian manifold, length of paths in 39
Riemannian manifold, open disk 40
Riemannian manifold, sphere in 40
Riemannian manifold, submanifold, cut point 320
Riemannian manifold, submanifold, focal point 320
Riemannian manifold, submanifold, mean curvature vector 310
Riemannian manifold, submanifold, normal bundle 224
Riemannian manifold, submanifold, second fundamental form 310
Riemannian manifold, submanifold, totally geodesic 131
Riemannian manifold, submanifold, Weingarten map 319
Riemannian manifold, surfaces, 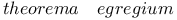 60 60
Riemannian manifold, surfaces, Gauss curvature 60
Riemannian manifold, surfaces, Gauss — Bonnet formula and theorem 60—61
Selberg trace formula 266—302
Selberg trace formula, pretrace formula 277
Selberg trace formula, pretrace formula, applications, electrostatics 282—288
Selberg trace formula, pretrace formula, applications, lattice-point estimates 279—281
Selberg trace formula, pretrace formula, applications, projections of dilating spheres 281—282
Selberg trace formula, trace formula 293
Selberg trace formula, trace formula, applications, Laplace and geodesic spectra 293 300
Selberg trace formula, trace formula, applications, small eigenvalues 300—302
Separation of variables, eigenfunctions and eigenvalues of disk in space form 40
Separation of variables, heat equation 12
Separation of variables, wave equation 11
surface 246
Surface, collar about geodesic 247
Surface, Riemann 246
Surface, Riemann, L bell 248—250 bell 248—250
Vector field, along path, derivative of 55
Vector field, along path, parallel 56
Vector field, along path, parallel translation of 57
Vector field, covariant derivative of 2
Vector field, divergence of 3
Vector field, transverse 319
Visibility angle 125
Volumes, disks and spheres 303—304
Wave equation, finite propagation speed 198
Wave equation, separation of variables 11
Weyl’s asymptotic formula 9
Weyl’s asymptotic formula, 1-dimensional problems 10
Weyl’s asymptotic formula, bounded domain in  31 31
Weyl’s asymptotic formula, closed eigenvalue problem 155
Weyl’s asymptotic formula, Dirichlet eigenvalue problem 172
Weyl’s asymptotic formula, forms 339
Weyl’s asymptotic formula, Poisson summation formula and 306—307
Weyl’s asymptotic formula, torus 30
Wiedersehnsraum 123
Wiedersehnsraum, Blaschke conjecture 123
Wirtinger inequality 130
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



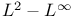 estimates
estimates  bell surfaces
bell surfaces 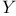 -piece
-piece  vy — Gromov
vy — Gromov