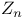|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Connell E.H. — Elements of abstract and linear algebra |
|
|
 |
| Предметный указатель |
Abelian group 20 71
Algebraically closed field 46 97
Alternating group 32
Ascending chain condition 112
Associate elements in a domain 47 109
Automorphism of groups 29
Automorphism of modules 70
Automorphism of rings 43
Axiom of Choice 10
Basis or free basis of a module 78 83
Basis or free basis, canonical or standard for  72 79 72 79
Bijective or one-to-one correspondence 7
Binary operation 19
Boolean algebras 52
Boolean rings 51
Cancellation law in a group 20
Cancellation law in a ring 39
Cartesian product 2 11
Cayley — Hamilton theorem 66 98 125
Cayley’s Theorem 31
Center of group 22
Change of basis 83
Characteristic of a ring 50
Characteristic polynomial of a homomorphism 85 95
Characteristic polynomial of a matrix 66
Chinese remainder theorem 50 108
Classical adjoint of a matrix 63
Cofactor of a matrix 62
Comaximal ideals 108 120
Commutative ring 37
complex numbers 1 40 46 47 97 104
conjugate 64
Conjugation by a unit 44
Contravariant functor 131
Coproduct or sum of modules 76
Coset 24 42 74
CYCLE 32
Cyclic group 23
Cyclic module 107
Determinant of a homomorphism 85
Determinant of a matrix 60 128
Diagonal matrix 56
Dimension of a free module 83
Division algorithm 45
Domain, Euclidean 116
Domain, integral domain 39
Domain, of a function 5
Domain, principal ideal 46
Domain, unique factorization 111
Dual basis 132
Dual spaces 130
Eigenvalues 95
Eigenvectors 95
Elementary divisors 119 120
Elementary matrices 58
Elementary operations 57 122
Endomorphism of a module 70
Equivalence class 4
Equivalence relation 4
Euclidean algorithm 14
Euclidean Domain 116
Evaluation map 47 49
Even permutation 32
Exponential of a matrix 106
Factorization domain (FD) 111
Fermat’s Little Theorem 50
Field 39
Formal power series 113
Fourier series 100
Free basis 72 78 79 83
Free R-module 78
Function or map 6
Function or map, bijective 7
Function or map, injective 7
Function or map, surjective 7
Function space  as a group 22 36 as a group 22 36
Function space  as a module 69 as a module 69
Function space  as a ring 44 as a ring 44
Function space  as a set 12 as a set 12
Fundamental theorem of algebra 46
Gauss 113
General linear group  55 55
Generating sequence in a module 78
Generators of 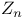 40 40
Geometry of determinant 90
Gram — Schmidt orthonormalization 100
Graph of a function 6
Greatest common divisor 15
Group 19
Group, abelian 20
Group, additive 20
Group, cyclic 23
Group, multiplicative 19
Group, symmetric 31
Hausdorff maximality principle 3 87 109
hilbert 113
Homogeneous equation 60
Homomorphism of quotient, group 29
Homomorphism of quotient, module 74
Homomorphism of quotient, ring 44
Homormophism of groups 23
Homormophism of modules 69
Homormophism of rings 42
Ideal, left 41
Ideal, maximal 109
Ideal, of a ring 41
Ideal, prime 109
Ideal, principal 42 46
Ideal, right 41
| Idempotent element in a ring 49 51
Image of a function 7
Independent sequence in a module 78
Index of a subgroup 25
Index set 2
Induction 13
Injective or one-to-one 7 79
Inner product spaces 98
Integers 1 14
Integers mod n 27 40
Invariant factors 119
Inverse image 7
Invertible or non-singular matrix 55
Irreducible element 47 110
Isometries of a square 26 34
Isometry 101
Isomorphism of groups 29
Isomorphism of modules 70
Isomorphism of rings 43
Jacobian matrix 91
Jordan block 96 123
Jordan canonical form 96 123 125
Kernel 28 43 70
Least common multiple 17 18
linear combination 78
Linear ordering 3
Linear transformation 85
Matrix, elementary 58
Matrix, invertible 55
Matrix, representing a linear transformation 84
Matrix, triangular 56
Maximal ideal 109
Maximal independent sequence 86 87
Maximal monotonic subcollection 4
Maximal subgroup 114
Minimal polynomial 127
Minor of a matrix 62
Module over a ring 68
Monomial 48
Monotonic collection of sets 4
Multilinear forms 129
Multiplicative group of a finite field 121
Nilpotent element 56
Nilpotent homomorphism 93
Noetherian ring 112
Normal subgroup 26
Odd permutation 32
Onto or surjective 7 79
Order of an element or group 23
Orthogonal group O(n) 102
Orthogonal vectors 99
Orthonormal sequence 99
Partial ordering 3
Partition of a set 5
Permutation 31
Pigeonhole Principle 8 39
Polynomial ring 45
Power set 12
Prime element 110
Prime ideal 109
Prime integer 16
Principal ideal 42
Principal ideal domain (PID) 46
Product of groups 34 35
Product of modules 75
Product of rings 49
Product of sets 2 11
Projection maps 11
Quotient group 27
Quotient module 74
Quotient ring 42
Range of a function 6
Rank of a matrix 59 89
Rational canonical form 107 125
Relation 3
Relatively prime, elements in a PID 119
Relatively prime, integers 16
Right and left inverses of functions 10
Ring 38
Root of a polynomial 46
Row echelon form 59
Scalar matrix 57
Scalar multiplication 21 38 54 71
Self adjoint 103 105
Short exact sequence 115
Sign of a permutation 60
Similar matrices 64
Solutions of equations 9 59 81
Splitting map 114
Standard basis for  72 79 72 79
Strips (horizontal and vertical) 8
Subgroup 14 21
Submodule 69
Subring 41
Summand of a module 77 115
Surjective or onto 7 79
Symmetric groups 31
Symmetric matrix 103
Torsion element of a module 121
Trace of a homormophism 85
Trace of a matrix 65
Transpose of a matrix 56 103 132
Transposition 32
Unique factorization domain (UFD) 111
Unique factorization of integers 16
Unique factorization, in principal ideal domains 113
Unit in a ring 38
Vector space 67 85
Volume preserving homomorphism 90
Zero divisor in a ring 39
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте




 as a group
as a group