|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Bennett C., Sharpley R.C. — Interpolation of Operators |
|
|
 |
| Предметный указатель |
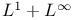 and and 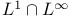 §2.6 74 §2.6 74
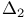 condition 266 condition 266
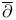 operator §5.9 §5.10 402 operator §5.9 §5.10 402
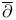 operator, fundamental solution 403 operator, fundamental solution 403
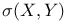 -topology 24 -topology 24
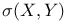 -topology, boundedness 24 -topology, boundedness 24
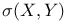 -topology, completeness 25 -topology, completeness 25
Absolutely continuous norm §1.3 14
Absolutely continuous norm and dominated convergence 16
Absolutely continuous norm and duality 23
Absolutely continuous norm and reflexivity 23
Absolutely continuous norm and separability 27 29
Admissible growth 209
Admissible norm 426
Admissible operator 99 115 301
Almost everywhere convergence §4.5 120 138
Analytic atom 435
Analytic family of operators §4.3 209
Approximate identity 178
Associate norm 8 12
Associate space 9
atom 369
Atomic decomposition 371 372
Average of a function 117 352
Averaging operator 57 61 150 202
B-spline 335
Banach function norm 2
Banach function norm, dominated convergence theorem 16
Banach function norm, Fatou property 4 6
Banach function norm, Fatou's lemma 5 6
Banach function norm, lattice property 6
Banach function space 3
Banach function space, 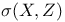 -completeness 25 -completeness 25
Banach function space, compactness 31
Banach function space, completeness 5
Banach function space, duality 23
Banach function space, reflexivity 23 30
Banach function space, separability 29
Banach limit 110
Banach's principle 237
Besov space §5.4 332 341
Bilinear form 188
Bilinear operator 255
Blaschke product 364 Appendix
BLO see "Bounded lower oscillation"
BMO see "Bounded mean oscillation"
Boundary function 364
Bounded lower oscillation 388
Bounded mean oscillation §5.6 368 §5.7 380 392
Bounded mean oscillation, decomposition into BLO functions 390 400
Boyd index see "Indices"
Boyd's theorem on the Hilbert transform 154
Boyd's theorem on weak-type operators 153
Brudnyi — Krugljak theory 326 429
Calderon couple 427
Calderon operator 133 142 153 163 176 222 256 262 313
Calderon operator and the Hilbert transform 138 387
Calderon operator and the maximal conjugate function 160
Calderon operator and the maximal Hilbert transform 134
Calderon operator and weak-type conditions 223 263 386
Calderon — Ryff theorem 114
Calderon's theorem on  and and 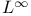 116 116
Calderon's theorem on weak-type operators 144
Carleson measure 401
Carleson norm 401
Characterizations of interpolation spaces 329 116 419 425
Class  310 310
Class  and log convexity 316 and log convexity 316
Compact operator 202
Compact operator and interpolation 203
Compatible couple 97
Complementary Young's function 271
Conditional expectations see "Averaging operator"
Conjugate couple 174
Conjugate, Poisson kernel 176 177
Conjugate-function operator 160 163 251
Convolution 155
Convolution operator 258 259
Covering lemma 121 377
Covering lemma, Vitali variant 118
Covering lemma, Whitney 348
Cwikel's formula for the K-functional 322
Decreasing rearrangement 39
Decreasing rearrangement of products 88
Decreasing rearrangement of sums 41
Decreasing rearrangement, properties 41
Decreasing rearrangement, radial 91
Decreasing rearrangement, signed symmetric 91
Decreasing rearrangement, symmetric 91
Density theorem 315
DeVore — Scherer theorem 360
Difference operator 331
Dilation operator 148
Distribution function 36
Distribution function, properties 37
Divisibility 325
Dominated Convergence Theorem 16
Duality §1.4 174
Duality for 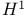 and BMO 374 and BMO 374
Duality for 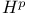 and Lip and Lip  433 433
Duality for 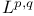 221 221
Duality for Orlicz spaces 275
Dyadic cubes 121
Elementary maximal function §2.3 52 219 377 382
Elementary maximal function and the Hardy — Littlewood maximal function 122
Elementary maximal function, properties 52 54 74
Embeddings, ( , q) interpolation spaces 300 301 316 , q) interpolation spaces 300 301 316
Embeddings, Banach function spaces 7 13 72 77 78
Embeddings, Besov and Lebesgue spaces 346
Embeddings, Besov and Sobolev spaces 334 346
Embeddings, BLO 389
Embeddings, BMO and Lebesgue spaces 382
Embeddings, BMO and weak-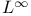 383 383
Embeddings, Lorentz spaces 217 286
Equimeasurable functions 37 80
Equivalence theorem 314
Exact interpolation pair 104 105
Extension operator 431
F* see "Decreasing rearrangement"
f** see "Elementary maximal function"
Fatou's lemma 6
Fefferman's duality theorem 374
Fejer kernel 179
Finite rank operator 202
Fourier coefficient 156 228
Fourier multiplier 159 163 433
Fourier series 156 179 285
Fourier transform 200 282
Fractional integral operator 228 254
Function norm see "Banach function norm"
Fundamental function §2.5 65 276 286
Fundamental function, properties 66 67
Fundamental indices see "Indices"
Gagliardo completion 296
Gagliardo couples 320
Hadamard three-lines theorem 195
Hardy space §5.6 §5.9 §5.10 363
Hardy space of rearrangement-invariant spaces 425
Hardy space, atomic 369
Hardy space, characterizations 372 432
Hardy space, real §5.6 365
Hardy — Littlewood inequality for rearrangements §2.2 44
Hardy — Littlewood maximal function see "Hardy — Littlewood maximal operator"
Hardy — Littlewood maximal operator §3.3 117 122 125 154 177 250 352
Hardy — Littlewood maximal operator and BMO 389
Hardy — Littlewood maximal operator and weak-type (1,1) 119 125
Hardy — Littlewood maximal theorem 125
Hardy — Littlewood theorem for Hardy spaces 364
Hardy — Littlewood — Polya relation 56 105 108 114 166 169 172 305 418
Hardy — Littlewood — Sobolev theorem 229
| Hardy's inequalities for averages 124
Hardy's inequalities for the Fourier transform 431
Hardy's Lemma 56
Hausdorff — Young theorem 200 283
Hilbert transform §3.4 126 138 154 366 367 372
Hilbert transform, Kolmogorov's theorem 139
Hilbert transform, Riesz's theorem 139
Hoelder's inequality 9 60
Hoermander condition 433
Holmstedt's formula 307
Indices for 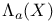 286 286
Indices for LlogL and 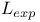 247 247
Indices for Lorentz spaces 218 220
Indices for Orlicz spaces 277
Indices, Boyd 149 165 177 178
Indices, fundamental 177
Intermediate space 99
Interpolating sequence 435
Interpolation inequality for derivatives 337
Interpolation method, maximal 429
Interpolation method, minimal 428
Interpolation of compact operators 203
Interpolation pair 102
Interpolation segment  141 141
Interpolation space §3.1 105
Interpolation space, ( ,q) space 299 301 §5.2 ,q) space 299 301 §5.2
Interpolation space, monotone §5.3 319
Interpolation spaces between 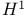 and and 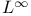 374 374
Interpolation spaces between 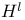 and and 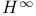 §5.10 415 §5.10 415
Interpolation spaces between  and and 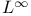 §3.2 116 305 §3.2 116 305
Interpolation spaces between  and BMO §5.8 398 and BMO §5.8 398
Interpolation spaces between  and and 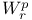 341 341
Interpolation spaces between ( ,q) spaces see "Reiteration theorem" ,q) spaces see "Reiteration theorem"
Interpolation spaces between Besov spaces 343
Interpolation spaces between Sobolev spaces §5.5 362
J-functional 293
J-method of interpolation 314 429
Jackson kernel 179
Jackson's theorem for rearrangement-invariant spaces 179
John — Nirenberg lemma for a cube 381
John — Nirenberg lemma for distribution functions 393
John — Nirenberg lemma for rearrangements 393
Joint weak type §3.5 143 253
Joint weak type and weak type (p, q) 223
Jones construction 405
K-functional 302 384
K-functional for 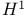 and and 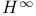 §5.10 411 414 §5.10 411 414
K-functional for  and and 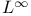 298 298
K-functional for  and BMO 393 and BMO 393
K-functional for  and the Sobolev space and the Sobolev space 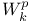 339 431 339 431
K-functional for ( ,q) spaces see "Holmstedt's formula" ,q) spaces see "Holmstedt's formula"
K-functional for C and Lip 1 436
K-functional for the Hardy space 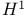 and and 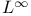 373 373
K-functional for the Sobolev spaces, 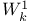 and and 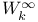 360 360
K-functional for the Sobolev spaces, 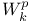 and and 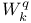 362 see 362 see
K-method 305 329
K-method of interpolation §5.1
Kernels for 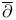 operator 404 405 operator 404 405
Kernels, Dirichlet 179
Kernels, Fejer 179
Kernels, Jackson 179
Kolomogorov's theorem 139
Landau's resonance theorem 10
Laplacian operator 402
Lattice property 6
Least concave majorant 70
Lebesgue differentiation theorem, multivariate case 430
Lebesgue differentiation theorem, univariate case 120
Lebesgue spaces 3
log convex estimate for Sobolev spaces 338
log convex estimate for spaces of class  316 316
Lorentz spaces, 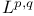 216 300 374 398 415 216 300 374 398 415
Lorentz spaces, 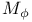 69 69
Lorentz spaces, 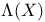 and M(X) 71 261 and M(X) 71 261
Lorentz spaces, 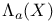 286 286
Lorentz — Luxemburg theorem 10
Lorentz — Shimogaki theorems 89 154 §3.7 169 173 329
Lorentz — Zygmund space 253 285
Lorentz' lemma 80
Luxemburg norm see "Orlicz spaces"
Luxemburg representation theorem 62
Marchaud's inequality 332 334
Marcinkiewicz interpolation theorem §4.4
Marcinkiewicz interpolation theorem and weak-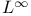 386 386
Marcinkiewicz interpolation theorem for Lebesgue spaces 226
Marcinkiewicz interpolation theorem for Lorentz spaces 225
Marcinkiewicz interpolation theorem, limiting case 248 253
Marcinkiewicz multiplier theorem 433
Maximal operator 237
Maximal operator, maximal conjugate function 160
Maximal operator, maximal Hilbert transform 127 130
Maximal operator, median 421
Maximal operator, nontangential 175 177 251 363 372 373 411
Maximal operator, radial 175
Maximal operator, signed 400
Measure-preserving transformations §2.7 80
Minimally smooth boundary 430
Modulus of continuity 157 332 431
Monotone, interpolation (intermediate) space §5.3 319
Monotone, Riesz — Fischer space 305 329
Moon's theorem 234
Multi-index 335
Multi-index differential operator 335
Multi-index length 335
Multilinear operator 201
Multilinear strong type interpolation 202
Multilinear weak type interpolation 255
Multiplier see "Fourier multiplier"
Nontangential maximal operator see "Maximal operator"
Norm-convergence of Fourier series §3.6 156 163
Norm-fundamental 12
Order ideal 16
Orlicz class 266
Orlicz space §4.8 270
Orlicz space, fundamental function 276
Orlicz space, indices 277
Orlicz space, Luxemburg norm 268
Orlicz space, Orlicz norm 273
Paley's theorem for Fourier series 228
Parseval's formula 200
Poisson integral 175
Poisson kernel 175 176 206 284 363
Positive integral operator 185
Q-maximal function 352
Quasiconcave 69
Quasilinear 143
Re 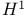 §5.6 365 §5.6 365
Rearrangement-invariant norm 59
Rearrangement-invariant space 59 116
Reduction Theorem 343
Reflexivity see "Banach function space"
Reiteration theorem 311 430
Relative Calderon pair 427
Relatively monotone 428
Resonant measure space 45 51 116
Restricted weak type §4.5 231 255 385
Retracts 54
Riesz convexity theorem for bilinear forms 189
Riesz convexity theorem for operators §4.1 192
Riesz — Fischer inequality for the Fourier transform 200
Riesz — Fischer norm 304 320 329
Riesz — Fischer property 6 32
Riesz — Fischer space 304
Riesz — Thorin convexity theorem §4.2 196
Riesz — Thorin convexity theorem, real version 199
Ryff's theorem 82
Ryff's theorem, counterexample 85
Separability §1.5
Separability and reflexivity 30
Separable measure 27
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



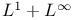 and
and 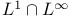
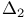 condition
condition 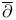 operator
operator 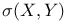 -topology
-topology 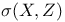 -completeness
-completeness  and
and 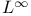

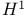 and BMO
and BMO 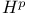 and Lip
and Lip 
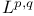
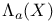
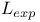

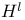 and
and 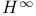
 and
and 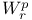
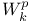
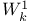 and
and 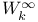
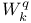
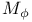
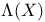 and M(X)
and M(X)