|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Joyce D.D. Ч Compact manifolds with special holonomy |
|
|
 |
| ѕредметный указатель |
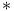 see Hodge star see Hodge star
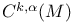 see H see H lder space lder space
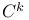 space 5 space 5
 -structure 38 -structure 38
 -manifold 243 -manifold 243
 -manifold, product 274 -manifold, product 274
 -manifold, QALE 272Ч278 -manifold, QALE 272Ч278
 -manifold, with holonomy SU(2) 271 -manifold, with holonomy SU(2) 271
 -manifold, with holonomy SU(3) 272 -manifold, with holonomy SU(3) 272
 -orbifolds -orbifolds 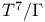 278Ч280 278Ч280
 -orbifolds -orbifolds 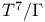 , examples 312 315 316 329 334Ч337 , examples 312 315 316 329 334Ч337
 -orbifolds -orbifolds 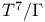 , R-data 280Ч281 , R-data 280Ч281
 -orbifolds -orbifolds 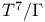 , resolutions of , resolutions of 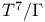 282Ч284 282Ч284
 -structure 243 -structure 243
 -structure, function -structure, function  243 249 243 249
 -structure, nearly parallel 269 -structure, nearly parallel 269
 -structure, positive 3-form 243 -structure, positive 3-form 243
 -structure, positive 4-form 243 -structure, positive 4-form 243
 -structure, small torsion 284 286 -structure, small torsion 284 286
 -structure, splitting of forms 244 245 -structure, splitting of forms 244 245
 -structure, torsion 243 -structure, torsion 243
 -structure, torsion-free 243 -structure, torsion-free 243
 holonomy 57Ч58 242Ч254 holonomy 57Ч58 242Ч254
 holonomy, associative 3-fold 70 264Ч265 326Ч327 417 holonomy, associative 3-fold 70 264Ч265 326Ч327 417
 holonomy, coassociative 4-fold 70 265Ч267 327Ч328 417 holonomy, coassociative 4-fold 70 265Ч267 327Ч328 417
 holonomy, compact manifolds, Betti numbers of 314 315 323 325 326 332Ч334 339 holonomy, compact manifolds, Betti numbers of 314 315 323 325 326 332Ч334 339
 holonomy, compact manifolds, constructions 294Ч295 303Ч305 holonomy, compact manifolds, constructions 294Ч295 303Ч305
 holonomy, compact manifolds, examples 309Ч326 329Ч338 holonomy, compact manifolds, examples 309Ч326 329Ч338
 holonomy, compact manifolds, finding holonomy, compact manifolds, finding 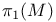 307Ч308 307Ч308
 holonomy, compact manifolds, finding Betti numbers 308Ч309 holonomy, compact manifolds, finding Betti numbers 308Ч309
 holonomy, compact manifolds, moduli space of 251Ч254 holonomy, compact manifolds, moduli space of 251Ч254
 holonomy, compact manifolds, topology of 245Ч247 306Ч309 holonomy, compact manifolds, topology of 245Ч247 306Ч309
 holonomy, compact manifolds, with holonomy, compact manifolds, with 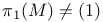 314Ч315 314Ч315
 holonomy, holonomy subgroups 245 holonomy, holonomy subgroups 245
 holonomy, metrics Ricci-flat 244 holonomy, metrics Ricci-flat 244
 holonomy, parallel spinors 245 holonomy, parallel spinors 245
 holonomy, research problems 303Ч305 416Ч418 holonomy, research problems 303Ч305 416Ч418
 , definition 242 , definition 242
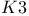 surface 155Ч162 surface 155Ч162
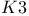 surface, examples 156 surface, examples 156
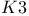 surface, marked 157 surface, marked 157
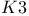 surface, moduli space 157 161 surface, moduli space 157 161
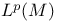 see Lebesgue space see Lebesgue space
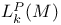 see Sobolev space see Sobolev space
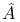 -genus 67 164 259 -genus 67 164 259
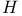 see Quaternions see Quaternions
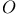 see Octonions see Octonions
Age grading 130Ч132 200
ALE manifold 173Ч174
ALE manifold, analysis on 178Ч182
ALE manifold, asymptotic coordinates 174
ALE manifold, Calabi conjecture for 186Ч188
ALE manifold, Eguchi Ч Hanson space 153Ч154 160
ALE manifold, examples 177Ч178 393Ч394
ALE manifold, Hodge theory 183Ч184
ALE manifold, holonomy Spin(7) 345Ч346
ALE manifold, hyperk hler 148 153Ч155 hler 148 153Ч155
ALE manifold, K hler 174 201 hler 174 201
ALE manifold, radius function 174 175
ALE manifold, Ricci-flat K hler 175Ч178 hler 175Ч178
ALE manifold, structure group Spin(7) 344 393Ч394
ALE manifold, weighted H lder space 176 179 lder space 176 179
ALE manifold, weighted Sobolev space 178
Ambrose Ч Singer Holonomy Theorem 32 37
Associative 3-fold 70 264Ч265 417
Associative 3-fold, examples 326Ч327
Asymptotically Locally Euclidean see ALE manifold
Atiyah Ч Singer index theorem 19 67 259
BergerТs Theorem 55
Betti number 2
Betti number, refined 62 245 260
Bianchi identities 36 43 45 59
Blow-up 91Ч92 293
Bochner theorem 64 124
Bootstrap method 116 303 364
Calabi Conjecture 98Ч100
Calabi conjecture, for ALE manifolds 186Ч188
Calabi conjecture, for QALE manifolds 225 229
Calabi Ч Yau manifold 56 70 82 98 121Ч147 304
Calabi Ч Yau manifold, constructions 138Ч142 146
Calabi Ч Yau manifold, definition 123
Calabi Ч Yau manifold, deformations 142Ч144
Calabi Ч Yau manifold, Hodge numbers 125
Calabi Ч Yau orbifold 135 146 395Ч396 401-
Calibrated geometry 68Ч70 264Ч269
Calibrated submanifold 68
Calibration 68
Canonical bundle 94
Cayley 4-fold 70 267Ч268 417
Cayley 4-fold, examples 371Ч373
Cayley numbers see Octonions
Characteristic class 94
Characteristic class, 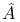 -genus 67 164 259 -genus 67 164 259
Characteristic class, first Chern class 94 97 98 122
Characteristic class, first Pontryagin class 246Ч247 259 261
Cheeger Ч Gromoll Theorem 64
ChowТs theorem 90 95 126
Coassociative 4-fold 70 265Ч267 417
Coassociative 4-fold, examples 327Ч328
Cohomology, de Rham 2 182
Cohomology, Dolbeault 77
Cohomology, Hodge numbers 85
Cohomology, of sheaves 89 93
Cohomology, other cohomology theories 2
Cohomology, Poincar duality 3 duality 3
Cohomology, with compact support 182
Compact linear map 6 103 179 187 226
Complete intersection 139 402 413
Complex manifold 72Ч75
Complex manifold, biholomorphism 74
Complex manifold, holomorphic function 72
Complex manifold, holomorphic map 74
Complex manifold, rigid 92 132 139
Complex projective space 73
Complex structure 72Ч73
Complex structure, almost 72
Complex symplectic manifold 162Ч164
Complex symplectic manifold, irreducible 162
Complex symplectic manifold, marked 163
Complex symplectic manifold, moduli space 163
Connection 20Ч25
Connection, Levi Ч Civita 40 42Ч43
Connection, on principal bundle 23
Connection, on tangent bundle 33Ч38
Connection, on vector bundle 22
Connection, torsion-free 35Ч38
Continuity method 104
Crepant resolution 126Ч132
Crepant resolution, of 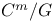 175 210 175 210
Curvature and holonomy groups 32Ч33
Curvature in principal bundles 24
Curvature in vector bundles 22Ч23
Curvature of K hler metrics 81Ч82 hler metrics 81Ч82
Curvature, Ricci 44
Curvature, Riemann 43Ч44
Curvature, scalar 44
de Rham theorem 2
Deformation 92Ч93
Deformation, of 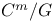 132 201 238 132 201 238
Deformation, of Calabi Ч Yau manifold 142Ч144
Deformation, smoothing 92 313 318 324
Deformation, universal 93
Deformation, versal 93
Dirac operator 65Ч68 259 260
Divisor 96Ч97
Divisor, exceptional 91 127
Divisor, prime 96
Dolbeault cohomology 77
Douady space 166 215
Double point 127
| Double point, ordinary 127
Double point, rational 129
EbinТs Slice Theorem 252
Eguchi Ч Hanson space 153Ч154 160 177 212 311 313 370 374
Elliptic equation nonlinear 250
Elliptic operator 7Ч19
Elliptic operator,  estimate 14 estimate 14
Elliptic operator, definition 9 11
Elliptic operator, existence of solutions 16Ч19
Elliptic operator, kernel finite-dimensional 17
Elliptic operator, nonlinear 10 100
Elliptic operator, regularity 13Ч16 297 303 364
Elliptic operator, Schauder estimate 14Ч15 180
Elliptic operator, symbol 9 11
Exterior form see Form
Fano manifold 168
FLOP 128
FORM 1Ч4
Form,  -structure splitting 59Ч60 -structure splitting 59Ч60
Form, Hermitian 78
Form, holomorphic volume 122
Form, hyperk hler 2-form 151 hler 2-form 151
Form, K hler 79 122 hler 79 122
Form, of type 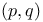 77 77
Form, on K hler manifolds 82Ч84 hler manifolds 82Ч84
Form,complex symplectic 150
Frobenius theorem 48
GreenТs representation 14 181
H lder space 5Ч6 lder space 5Ч6
H lder space, weighted 176 179 221 lder space, weighted 176 179 221
H lderТs inequality 4 lderТs inequality 4
Harmonic coordinates 298
Hilbert scheme 166 215
Hodge numbers 85
Hodge numbers, of hyperk hler manifolds 164 hler manifolds 164
Hodge star 3 60
Hodge star, on K hler manifolds 83 hler manifolds 83
Hodge theory 4 61Ч63
Hodge theory, on ALE manifolds 183Ч184
Hodge theory, on K hler manifolds 84Ч85 hler manifolds 84Ч85
Holomorphic vector bundle 77
Holonomy algebra 28 30 45
Holonomy group, and cohomology 59Ч64
Holonomy group, and curvature 32Ч33
Holonomy group, classification 55Ч59
Holonomy group, constant tensors 34Ч35
Holonomy group, definition 26 29 45
Holonomy group, exceptional see  holonomy Spin(7) etc. holonomy Spin(7) etc.
Holonomy group, for principal bundles 29Ч32
Holonomy group, for vector bundles 25Ч29
Holonomy group, restricted 28 29 45
Holonomy group, Ricci-flat 58
Holonomy group, Riemannian 44Ч45
Hypercomplex algebraic geometry 171 215
Hypercomplex manifold 148 167 170
Hyperk hler manifold 57 98 148Ч167 169 hler manifold 57 98 148Ч167 169
Hyperk hler manifold, ALE 148 153Ч155 hler manifold, ALE 148 153Ч155
Hyperk hler manifold, examples 165Ч167 hler manifold, examples 165Ч167
Hyperk hler manifold, Hodge numbers 164 hler manifold, Hodge numbers 164
Hyperk hler manifold, moduli space 165 hler manifold, moduli space 165
Hyperk hler manifold, QALE 211 213Ч215 239 hler manifold, QALE 211 213Ч215 239
Hyperk hler manifold, twistor space 151Ч152 hler manifold, twistor space 151Ч152
Hyperk hler quotient 154 169 hler quotient 154 169
Hyperk hler structure 148 151 hler structure 148 151
Hypersurface 96
Hypersurface, Calabi Ч Yau 139
Hypersurface, degree 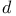 139 139
Hypersurface, in toric variety 142
Hypersurface, in weighted projective space 140 401
Implicit Mapping Theorem 7 253 263
Injectivity radius 5 221 292Ч295 298 359- 399
Instanton 169 269
Interior estimate 16
Intrinsic torsion 40
Inverse mapping theorem 7 118 228
K hler chamber 158 hler chamber 158
K hler class 80 85 175 210 hler class 80 85 175 210
K hler cone 85 158 175 210 hler cone 85 158 175 210
K hler form 79 122 hler form 79 122
K hler manifold 56 hler manifold 56
K hler metric 79 hler metric 79
K hler potential 80 hler potential 80
K hler potential type 215 229 hler potential type 215 229
Kodaira embedding theorem 96 125
Kondrakov Theorem 7 16 103
Kummer construction 137 156Ч157 160Ч161
Kuranishi family 94 143
Laplacian 3 7 10 14 61
Laplacian, on ALE manifolds 180Ч182
Laplacian, on K hler manifolds 83 105 198 hler manifolds 83 105 198
Laplacian, on QALE manifolds 220Ч225
Lebesgue space 4Ч5
Lefschetz hyperplane theorem 97 140 404
Levi Ч Civita connection 40 42Ч43
Line bundle 94Ч96
Line bundle, ample 95 125
Line bundle, canonical 94 122 126
Line bundle, first Chern class 94 97 98 122
Line bundle, over 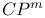 94 94
Line bundle, positive 96
Line bundle, very ample 95
Maximum principle 16 222
McKay correspondence 129 131 154 309
Metric, Fubini Ч Study 53 80
Metric, Hermitian 78
Metric, hyperk hler 151 hler 151
Metric, K hler 79 hler 79
Metric, reducible 46Ч50
Metric, symmetric 50Ч55
Mirror Symmetry 142 145Ч146
Moduli space 63 169
Moduli space, of  -manifolds 251Ч254 -manifolds 251Ч254
Moduli space, of 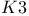 surfaces 157 161 surfaces 157 161
Moduli space, of complex symplectic manifolds 163
Moduli space, of hyperk hler manifolds 165 hler manifolds 165
Moduli space, of Spin(7)-manifolds 261Ч264
Monge Ч Amp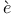 re equation 100 re equation 100
Newlander Ч Nirenberg theorem 72
Nijenhuis tensor 72
Node 127
Octonions 57
Orbifold 132Ч136
Orbifold, Calabi Ч Yau 135 146 395Ч396 401^02
Orbifold, complex 133 166
Orbifold, crepant resolntion 136Ч139
Orbifold, group 133
Orbifold, K hler 134 hler 134
Orbifold, of torus 137 278Ч280 346Ч347
Orbifold, point 133
Orbifold, real 133
Parallel transport 26
Period domain 158 163
Period domain, hyperk hler 161 165 hler 161 165
Period map 143 157 163
Period map, hyperk hler 161 165 hler 161 165
Picard group 94
Poincar duality 3 duality 3
Principal bundle 20
Principal bundle, connection 23
QALE manifold, analysis on 219Ч225
QALE manifold, Calabi conjeclure for 225 229
QALE manifold, definition 208 236Ч238
QALE manifold, examples 212Ч215 239Ч241 276Ч278
QALE manifold, generalized 235Ч241
QALE manifold, holonomy  277Ч278 277Ч278
QALE manifold, holonomy Sp(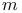 ) 211 213Ч215 239 ) 211 213Ч215 239
QALE manifold, holonomy Spin(7) 345Ч346
QALE manifold, holonomy SU(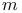 ) 211Ч213 239 ) 211Ч213 239
QALE manifold, K hler 208Ч210 238 hler 208Ч210 238
QALE manifold, K hler potentials 215 hler potentials 215
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



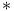
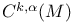
 lder space
lder space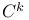 space
space  -structure
-structure  -manifold
-manifold 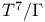

 holonomy
holonomy 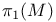
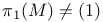
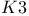 surface
surface 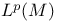
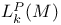
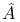 -genus
-genus 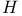
 hler
hler  duality
duality 
 estimate
estimate 
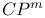
 re equation
re equation  )
)