|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Peszat S., Zabczyk J. — Stochastic partial differential equations with Levy noise: An evolution equation approach |
|
|
 |
| Предметный указатель |
Tempered distributions 240
Theorem, Aronson 18
Theorem, Bochner 72
Theorem, Borel Isomorphism 4
Theorem, Caratheodory 23
Theorem, Courrege 8
Theorem, De Acosta 39
Theorem, Delbaen — Schachermayer 327
Theorem, Dilation 160
Theorem, Doob regularity 33
Theorem, Doob — Meyer 35
Theorem, Douglas 364
Theorem, Dynkin 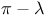 20 20
Theorem, Femique 30
Theorem, Frobenius — Perron 302
Theorem, Hille — Yosida 365
Theorem, Ito — Nisio 23
Theorem, Kinney 27
Theorem, Kolmogorov 22
Theorem, Kruglov 39
Theorem, Krylov — Bogolyubov 288
Theorem, Kuratowski — Ryll — Nardzewski 114
Theorem, Lumer — Phillips 366
Theorem, Skorokhod embedding 5
Theorem, Tauberian 315
Theorem, Tortrat 74
Theorem, Ulam 23
| Tortrat theorem 74
Trace 357
Trace operator 8
Trajectory 3 5
Transition function 3
Transition probability 3 6 10
Transition semigroup 7
Translation operator 84
Translations on S'(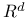 ) 246 ) 246
Two-sided exponentially tempered stable coordinates 64
Ulam theorem 23
Uniform integrable sequence 25
Uniform motion 78
Usual conditions 22
Variation-of-constants formula 140
Volatility 333
Weighted spaces 15
Weights, exponential 15
Weights, polynomial 15
White noise, discrete-time 4
White noise, Gaussian space-time 98
White noise, impulsive 100—105
Wiener process 44
Wiener process with respect to filtration 44
Wiener process, cylindrical 97
Wiener process, standard 44
Wong — Zakai correction term 351
Yosida approximation 180 184 365
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 )
)