|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Stakgold I. — Green's functions and boundary value problems |
|
|
 |
| Предметный указатель |
Matrix 297
Maximum principle 64 498 593 610
Maximum principle, for diffusion 495
Maximum principle, for harmonic functions 66 507
Mean value property 507
Measurable 37
Measure 37
Mellin transform 466 519
Mercer’s theorem 376
Method of continuity 567
Metric 234
Metric spaces 233—243
Metric spaces, complete 235
Metric spaces, completion of 238 241
Metric, 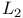 238 238
Metric, equivalent 242
Metric, natural 260
Metric, uniform 238
Minimum potential energy 522
Minimum principle see Maximum principle
Monotone iteration 581 593 608—621 627
Multi-index 89
Multiplication factor 25 620
Multiplicity 325
Neumann problem 519
Neumann series 249 378—380
Neutron diffusion 30 84
Neutron transport 25 355 620
Newton’s Law of Cooling 6
Newton’s method 563 637
Norm 259
Normalization of eigenfunctions 418 434
Null sequence 90 154 161
Null space 208
One-sided functions 150
One-to-one 223
Onto 222
Open set 1
Operators 295
Operators, adjoint of 313 315
Operators, bounded 295
Operators, bounded away from zero 308
Operators, bounded below or above 342 433
Operators, closable 304
Operators, closed 305 310
Operators, closure of 305
Operators, coercive 342
Operators, compact 335 345
Operators, continuous 296
Operators, differentiation 301
Operators, domain of 295
Operators, extension of 304
Operators, extremal properties of 339—346
Operators, Fr chet derivative of 579 chet derivative of 579
Operators, indefinite 374
Operators, inverse 308
Operators, linearization of 578
Operators, nonnegative 342 374
Operators, norm of 296
Operators, null space of 295 306
Operators, positive 342 374
Operators, range of 295
Operators, regular 309
Operators, self-adjoint 315
operators, shift 302
Operators, state of 309
Operators, strictly positive 342
Operators, symmetric 315
Operators, unbounded 296 (see also Spectrum; Transformations)
Operators, with closed range 320
Order interval 581
Orthogonal 208 264
Orthogonal complement 266
Orthogonal, with weight 285
Orthogonality condition see Solvabilitty conditions
Orthonormal basis 269
Orthonormal set 127 264
Orthonormal set, complete 269
Orthonormal set, maximal 282
P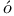 lya’s isoperimetric inequality 549 lya’s isoperimetric inequality 549
Parabolic equations 475 488—498
Parallelogram law 264 274
Parseval's identity 129 134 282
Partial differential equations, Cauchy problem 468 469 476
Partial differential equations, classification 467—482
Partial differential equations, elliptic 475 501
Partial differential equations, hyperbolic 475 482
Partial differential equations, parabolic 475
Partial differential equations, semilinear 472 474
Payne — Rayner inequality 562
Peclet number 12
Perturbation methods 569 591—602
Poincar maximin theorem 397 maximin theorem 397
Poincar — Keller method 607 — Keller method 607
Poisson equation 505 546
Poisson kernel 113 121 122 504
Poisson summation formula 140 492
Polar identity 275
Pole 94 177
Pollack, H. O. 387
Potential theory see Laplace’s equation
Principal part of operator 468
Principal value of square root 62 420
| Principle of linearized stability 623
Projection 265 266
Projection theorem 266 281
Pseudo function 102
Pseudo inverse 218 595 598 605
RANGE 222
Rayleigh quotient 339 392
Reciprocity principle 200
Reciprocity relation 526
Relatively compact set 241 335
Representative sequence 528
Resolvent set 324
Resonance index 382
Riemann integral 36
Riemann — Lebesgue lemma 108 122 129 133
Riesz representation theorem 292 294
Riesz — Fischer theorem 278
Ritz — Rayleigh approximation 394 539
Rods 14
Sampling formula 146
Scattering 27
Schwarz inequality 262 263 271 272 525
Schwarz iteration 400 405
Schwinger — Levine principle 539
Self-adjoint 315 354
Self-adjoint, boundary value problem 198 205
Self-adjoint, formally 100 168 170
Sifting property 54
Similarity solution 499 500
Simple layer 96 509
Singular point 185 467
Slepian, D. 387
Sobolev spaces 272 532
Solutions, classical 46 172
Solutions, distributional 173
Solutions, lower 504
Solutions, maximal 565
Solutions, upper 564
Solutions, weak 173 176 524
Solvability conditions 208 320—323 382
Span, algebraic 229 276
Span, closed 276
Spanning set 276 277
Specific heat 3
Spectrum 324
Spectrum, approximate 325
Spectrum, compression 325
Spectrum, continuous 325 451
Spectrum, of compact, self-adjoint operator 369—375
Spectrum, point 324
Sphere 1
Stability 621—631
Stefan — Boltzmann law 254
Step response 191
strings 14
Strong 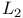 derivative 532 derivative 532
Successive approximations 243
Superposition principle 42 193 201
Support 90 164
Supremum 2
Surface layers 508—513
Symmetrization 561
Symmetry of compact operator 354
Symmetry of kernel 315
Symmetry of matrix 315
Symmetry of operator in Hilbert space 315
Test functions of compact support 87
Test functions of rapid decay 153 161
thermal conductivity 3
Thermal diffusivity 4
Theta function 492
Torsional rigidity 546
Trace inequality 377
Transformations 223 224
Transformations, continuous 241
Transformations, linear 225 (see also Operators)
Transposed matrix see Adjoint matrix
Transversal 181
Triangle inequality 234
Unforced 583
Unilateral constraints 552—558
Uniqueness 56 193 244 495 499
Variance 400
Variational equation 524 526
Variational inequality 554 557
Variational principles, complementary 545
Variational principles, for inhomogeneous problems 520—562
Variational principles, for operators 339—346 392—399
Variational principles, Schwinger — Levine 539
Vector space see Linear space
Vibrations of rod 14 24
Vibrations of string 20 24
Volterra integral equation 249 388
Wave equation 175 475 481
Wave operator 171
Weber transform 465
Weierstrass approximation theorem 113 120 240 284 289
Weinstein, A. 398
Well posed 58 482
Weyl — Courant minimax theorem 393 434
Weyl’s theorem 438
Wiener — Hopf method 350
wronskian 187
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



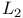
 chet derivative of
chet derivative of  lya’s isoperimetric inequality
lya’s isoperimetric inequality