|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Tuynman G.M. — Supermanifolds and Supergroups: Basic Theory |
|
|
 |
| Предметный указатель |
 -Lie algebra 270 -Lie algebra 270
 -Lie algebra, associated to an -Lie algebra, associated to an  -Lie group 271 -Lie group 271
 -Lie group 142 266 -Lie group 142 266
 -Lie subgroup 292 -Lie subgroup 292
 -Lie subgroup, normal 296 -Lie subgroup, normal 296
 -Lie subgroup, proper 300 -Lie subgroup, proper 300
 -manifold 128 -manifold 128
 -module 2 -module 2
 -vector space 85 -vector space 85
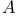 -graded -graded  -module 6 -module 6
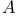 -graded commutative ring 3 -graded commutative ring 3
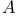 -graded commutativity 3 -graded commutativity 3
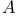 -graded ring 3 -graded ring 3
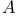 -grading 3 -grading 3
Action, effective 143
Action, left/right 142 266
Adjoint representation 31 32 283 284 325
Affine connection 374
Algebra, 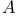 -graded commutative 28 -graded commutative 28
Algebra, 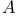 -graded Lie 28 -graded Lie 28
Algebra, 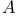 -graded Lie of parity -graded Lie of parity  31 31
Algebra, associative 28
Algebra, associative of parity  32 32
Associated bundle 151 364
Atlas 124
Atlas, adapted to a subbundle 160
Atlas, trivializing 145
Automorphism of a module 11
Basis 46
Basis, dual 67
Basis, ordered 59
Basis, orthonormal 192
Batchelor's theorem 196
Berezinian 41 55 78
Bianchi identities 355 357
Bilinear map 8
Bimodule 2
Body of  57 57
Body of a (proto)  -manifold 126 -manifold 126
Body of a linear map 82
Body of a matrix 58
Body of a module 82
Body of a smooth function 105 129
Border point 228
Bracket of a Lie algebra 28
Bundle of morphisms 170
Bundle, associated 151 364
Bundle, fiber 145
Bundle, fiber, principal 155 301
Bundle, frame 361
Bundle, pull-back 151
Bundle, structure 361
Bundle, trivial 147
Bundle, vector 156
Cartan's structure equations 355 357—359
Center of a Lie algebra 325
Central extension of a Lie algebra 325
Central extension of an  -Lie group 325 -Lie group 325
Chain rule 116
Chart of an  -manifold 124 -manifold 124
Christoffel symbols 370
Closed differential form 262
Cocycle of a Lie algebra 325 332
Cocycle of an  -Lie group 325 -Lie group 325
Cohomology of a Lie algebra 325 332
Cohomology of an  -Lie group 325 332 -Lie group 325 332
Cohomology, de Rham 263 327
Commutativity, 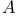 -graded 3 -graded 3
Commuting flows 236
Compatible chart of a fiber bundle 144
Compatible chart of an  -manifold 124 -manifold 124
Complex conjugation 188
Connection 342 345 351
Connection, 1-form 351
Connection, affine 374
Connection, Ehresmann 342
Connection, flat 342
Connection, FVF 345
Connection, integrable 342
Connection, linear 374
Connection, principal 351
Contraction, elementary 74 75 274
Contraction, operator 12
Convergence 286
Coordinate (even/odd) 104
Cotangent bundle 248
Covariant derivative 366
Covariant derivative, exterior 354
Covariant derivative, induced 368
Covering 311—312
Coxeter group 23
Curvature 2-form 355
Curvature tensor 394
De Rham cohomology 263 327
Decomposition 2
Degree- part of a vector bundle 167 part of a vector bundle 167
Derivation (right/left) 29
Determinant 41 61 77 80 111
Determinant, graded 41 55 78—80 111 118 285
DeWitt topology 93
Diffeomorphic 128
Diffeomorphism 128
Differential form 248
Differential form with values in a vector bundle 383
Differential form with values in an  -vector space 323 -vector space 323
Dimension of a (proto)  -manifold 124 -manifold 124
Dimension, differential 207
Dimension, even/graded/odd/total 61
Direct product of  -manifolds 133 -manifolds 133
Direct product of bundles 153
Direct sum 7 14
Direct sum of bundles 164
Dual basis 67
Dual bundle 170
Dual of a module 9
Dual of a morphism 14
Effective action 143
Ehresmann connection 342
Elementary contraction 74 75 274
Embedding 214
Endomorphism 9
Enlarging the structure group 154
Equivalence of  -Lie subgroups 293 -Lie subgroups 293
Equivalence of bases 83
Equivariant map 305
Euler vector field 261
Evaluation operator 12
Even 3 4 56
Exact differential form 262
example 3 4 21 28 56 57 59 71 74 97 110 118 125 132 133 137 143 144 152 231 280 283 287 297 332 339 367 396 399
Example, counter 7 10 60 63 65 66 76 81 84 87 103 123 130 148 163 191 192 216 221 224 244 300 344
Exponential map 278
Exponential map of matrices 287
Exterior algebra 27
Exterior covariant derivative 354
Exterior derivative 249
Exterior power 25
Exterior power of a vector bundle 167
f.g.p 47—54 59 172 180 181 196 250
Family of  -Lie group morphisms 282 -Lie group morphisms 282
Family of Lie algebra morphisms 282
Fiber, bundle 145
Fiber, bundle, map 147
Fiber, bundle, principal 155 301
Fiber, bundle, structure 145
Fiber, over a point 145
Fiber, typical 145
Finite dimensional 59
Finite type 46
Finitely generated 46 48 50 51 196
| Flat connection 342
Flow 228
Flow, commuting 236
Flow, global 234
Flow, local 228
Foliation 243 341
Form, differential k- 248
Frame 361
Frame, bundle 361
Free 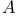 -graded -graded  -module 16 -module 16
Frobenius' Theorem 243 244 342 355
Fundamental vector field 299
FVF connection 345
Gauge 351
Gauge, transformation 351
Generator 16 46
Graded 56
Graded, determinant 41 55 78—80 111 118 285
Graded, subspace 59 86
Graded, trace 75 76 80 285
Graded, transpose 71
Graph 134 149
Homogeneous 3 4
Homomorphism 9
Horizontal k-form 395
Horizontal lift 342
Horizontal map 342
Horizontal part of a tangent vector 342
Horizontal section 342
Horizontal submanifold 342
Horizontal tangent vector 342
Ideal 296
Identification 11
Immersion 214
Implicit function theorem 122
Independent elements 46
Initial condition 228
Integrable connection 342
Integrable subbundle 243 244 342
Integrable vector field 228
Integral manifold 244
Interchanging map 22
interval 228
Invariance of dimension 121
Invariant k-form 320
Invariant k-form, left/right 320
Invariant vector field 315
Inverse function theorem 121
Invertible homomorphism 11
Involutive subbundle 243
Isomorphic fiber bundles 147
Isomorphic modules 11
Isomorphism 11
Isomorphism of  -Lie groups 267 -Lie groups 267
Isomorphism of fiber bundles 147
Isomorphism of Lie algebras 270
Isomorphism of vector bundles 157
Isotropy subgroup 304
Jacobi identity 28 30—32 270—272 284 326 332 356
Jacobian 116
k-additive 2
k-form 248
k-form with values in a vector bundle 383
k-form with values in an  -vector space 323 -vector space 323
k-form, M-dependent 257
k-linear map (left/right) 8
Kronecker delta 58
Leaf 244 246 294
Left multiplication 2
Left translation 268
Left-invariant vector field 270
Lie derivative 253
Lift 377
Linear connection 374
Linear map (left/right) 8
Local flow 228
Locally finite 134
Maurer — Cartan 1-form 339 357
Metric on a free graded  -module 192 -module 192
Metric on a vector bundle 194
Modeled, an  -manifold on an -manifold on an  -vector space 124 -vector space 124
Module 2—6
Momentum map 332
Morphism 9
Morphism of  -Lie groups 142 267 -Lie groups 142 267
Morphism of Lie algebras 30 270
Morphism of vector bundles 157
Nilpotent vector 81
Normal  -Lie subgroup 296 -Lie subgroup 296
Notational shorthand 119
Odd 56
Ordered basis 59
Orthogonal complement 193
Orthonormal basis 192
Parallel transport 344 364
Parity 3 4
Parity of a linear map 8
Parity of a section 158
Parity, reversal 102
Parity, shift operation 32 102
Partition of unity 95 128 135 136 159 167 175 194 195 197 199 263
Plateau function 136 160 176 205 250 327
Principal connection 351
Principal fiber bundle 155 301
Product of bundles 153
Projective 47
Proper  -Lie subgroup 300 -Lie subgroup 300
Proto  -manifold 124 -manifold 124
Pseudo effective action 143
Pseudo metric on a vector bundle 194
Pseudo metric, pseudo metric on a free graded  -module 188 -module 188
Pull-back of a differential form 255
Pull-back of a differential form, E-valued 324
Pull-back of a differential form, generalized 257 319
Pull-back of a section 183
Pull-back, bundle 151
Pull-back, map 183
Push forward of a section 178
Push forward of a vector field 218
Quotient 16
Quotient, bundle 164
Rank 73
Rank of a function 122
Rank of a matrix 58
Rank of a vector bundle 156
Reducing the structure group 154
Regular value 214
Related vector fields 218
Representation of a Lie algebra 30
Representation of an  -Lie group 267 -Lie group 267
Restriction of a bundle to a submanifold 146
Right multiplication 2
Right translation 268
Right-invariant vector field 270
Ring, 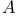 -graded 3 -graded 3
Ring, commutative 3
Second countable topology 128 245 247
Section 148
Shorthand, notational 119
Signature 24
Simply connected 312
Skew-symmetric 24
Skew-symmetrization operator 40
Smooth  -structure 124 -structure 124
Smooth functions 94—101
Smooth linear map 85
Smooth map between  -manifolds 128 -manifolds 128
Smooth system 96
Smooth system, maximal 97
Smooth tree 96
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -Lie algebra
-Lie algebra 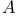 -graded
-graded 