|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Smart N.P. — The algorithmic resolution of Diophantine equations |
|
|
 |
| Предметный указатель |
Pythagorean triples 2
Pythagorean triples 2
Quadratic form 66 171 181 186 216
Quadratic form 66 171 181 186 216
Quadratic form, binary 5 54 55 112 114 151 172 184
Quadratic form, binary 5 54 55 112 114 151 172 184
Quadratic form, quarternary 211
Quadratic form, quarternary 211
Quadratic form, ternary 46 51 54 112 114 171 172 184
Quartic form 184 188
Quartic form 184 188
Quartic form, covariants 188
Quartic form, covariants 188
Quartic form, invariants 187
Quartic form, invariants 187
R mond, G. 210 mond, G. 210
R mond, G. 210 mond, G. 210
Ramanujan — Nagell equation 6
Ramanujan — Nagell equation 6
Ramanujan, S. 6
Ramanujan, S. 6
Ribet, K. 221
Ribet, K. 221
Rose, H. viii
Rose, H. viii
Schmidt, W. M. 105
Schmidt, W. M. 105
Selmer group 185
Selmer group 185
Selmer, E. 40
Selmer, E. 40
Seminvariants 188
Seminvariants 188
Serre, J. P. 221
Serre, J. P. 221
Shimura — Tamyama — Weil conjecture 193 222
Shipsey, R. xii
Shorey, T. vii
Shorey, T. vii
Siegel, C. L. 99 134
Siegel, C. L. 99 134
Siegel’s identity 36 37
Siegel’s identity 36 37
Siksek, S. xii 51 191
Siksek, S. xii 51 191
Silverman, J. H. 23 181 191
Silverman, J. H. 23 181 191
SkoJem, Th 5 36
SkoJem, Th 5 36
Skolem’s method 33 36-39 97 103 105
Skolem’s method 33 36-39 97 103 105
Stephens, N. xii 206
Stephens, N. xii 206
Strassmann’s theorem 25 33-36 218
Strassmann’s theorem 25 33-36 218
Stroeker, R. 206
| Stroeker, R. 206
Subexponential Time 8 48
Subexponential Time 8 48
Superelliptic curve 220
Superelliptic curve 220
Tate — Shaferevich group 185
Tate — Shaferevich group 185
Tate, J. 181
Tate, J. 181
Thue equation ix 7 33-36 38 45 97 99-117 120 122 129 133 135 137 151 170-173 197 211 220
Thue equation ix 7 33-36 38 45 97 99-117 120 122 129 133 135 137 151 170-173 197 211 220
Thue — Mahier equation ix 97 117 135 137 151 153 161
Thue — Mahier equation ix 97 117 135 137 151 153 161
Thue, A. 7 97
Thue, A. 7 97
Tijdeman, R. vii 223
Tijdeman, R. vii 223
Triangularly connected decomposable form 153-163 165 167 173 220
Triangularly connected decomposable form 153-163 165 167 173 220
Tzanakis, N. 97 98 105 117 210
Tzanakis, N. 97 98 105 117 210
Urfels, F. 210
Urfels, F. 210
Van der Poorten, A. J. 124
Van der Poorten, A. J. 124
Vpurely periodic 61
W stholz, G. 9 137 138 148 225 stholz, G. 9 137 138 148 225
W stholz, G. 9 137 138 148 225 stholz, G. 9 137 138 148 225
Waldschmidt, M. 9
Waldschmidt, M. 9
Weak form 182-186 188-190
Weak form 182-186 188-190
Weierstrass 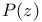 -function 198 -function 198
Weierstrass 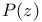 -function 198 -function 198
Weierstrass long form 177-179 202
Weierstrass long form 177-179 202
Weierstrass short form 179 183 215
Weierstrass short form 179 183 215
Weierstrass, K. 5
Weierstrass, K. 5
Weil, A. 180
Weil, A. 180
Wildanger, K. 133
Wildanger, K. 133
Wiles, A. 1 193 221 222
Wiles, A. 1 193 221 222
Wright, E. H. 59
Wright, E. H. 59
Yu, K. 9 226
Yu, K. 9 226
Yu’s theorem 121 123 141 226
Yu’s theorem 121 123 141 226
Zagier, D. 201 205 210
Zagier, D. 201 205 210
Zassenhaus, H. viii
Zassenhaus, H. viii
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 mond, G.
mond, G.  stholz, G.
stholz, G. 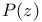 -function
-function