|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| A. Prestel, P. Roquette — Formally p-adic Fields |
|
|
 |
| Предметный указатель |
 -adic Analog of Hilbert’s -adic Analog of Hilbert’s 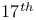 Problem 148 149 Problem 148 149
 -adic closure 8 33 -adic closure 8 33
 -adic Kochen operator of type (e,f) 92 -adic Kochen operator of type (e,f) 92
 -adic topology 124 -adic topology 124
 -adic transfer principle 10 -adic transfer principle 10
 -adically closed 8 33 84 -adically closed 8 33 84
 -divisibility 6 -divisibility 6
 -ramification index 13 -ramification index 13
 -rank 13 83 -rank 13 83
 -valuation 7 -valuation 7
 -valuation of type (e,f) 93 -valuation of type (e,f) 93
 -valued field 7 -valued field 7
 -valued field of -valued field of  -rank d 13 -rank d 13
 — Kochen ring 102 — Kochen ring 102
 -saturated 6 2 -saturated 6 2
 -group 9 8 5 -group 9 8 5
 -adic Kochen operator 122 -adic Kochen operator 122
 -adic Kochen operator of type (e,f) 95 -adic Kochen operator of type (e,f) 95
(relative) initial index 23 94
Absolute value 1
Algebraic Embedding Theorem 53
Artin 2
Ax 5
Axiom, universal 83
Base field 93
Basic subset 125
Bezout ring 117
Canonical decomposition 24
Characterization Theorem,  -adic 9 -adic 9
Characterization Theorem, real 4
Coarse valuation 25
Completeness 89
Convex subgroup 1 4
Core field 26
Core valuation 27
Decidability 5 87 89
Decomposition, canonical 24
Defect 29
Defining relation 52
Definite, integral 123 144 149
Definite, positive 2
Denter 100
Dimension (of a place) 123
Eisenstein polynomial 39
Elementary equivalence theorem 90
Elementary extension 86
Embedding Theorem for regular extensions 65
Embedding Theorem, Algebraic 53
Er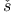 ov 5 ov 5
Formally  -adic 7 92 -adic 7 92
Formally  -adic of type (e,f) 93 -adic of type (e,f) 93
Formally  -adic over 93 125 -adic over 93 125
Formally real 4 92
General Embedding Theorem 63
Henselian 20
Henselization 21
Hensel’s Lemma 8 20
Hilbert’s 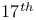 Problem 2 Problem 2
Holomorphic at 134
Holomorphy ring 104 134
Immediate extension 21
Initial index 23 94
Integral definite 123 144 149
Isomorphism Theorem for  -adic closures 9 -adic closures 9
Isomorphism Theorem for algebraic extensions 57
Isomorphism Theorem for real closures 4
Kochen 5
Kochen operator 8
Kochen operator,  -adic 92 -adic 92
Kochen operator,  -adic 95 122 -adic 95 122
Kochen operator,  -adic of type (e,f) 95 -adic of type (e,f) 95
Kochen ring over 135
Kuhlmann 142
Language, modified 84
Language, of valued fields 83
Laurent series (formal) 16
Level of a unit 45
lexicographical ordering 15
| MacIntyre 91
McKenna 149
Merckel’s Lemma 102 135 153
Model completeness (of real closed fields) 5
Model Completeness Theorem 86
Modified language 84
Nakayama’s Lemma 111
Newton’s Lemma 20
Non-principal ultra filter 18
Nullstellensatz 143
Ordering 2
Place Existence Theorem 125
Place, rational 124
Positive definite 2
Priifer ring 117
Prime element 13
Principal ideal theorem 118
Puiseux series 16
Quantifier Elimination Theorem 91
Radical element 48
Radical group 48
Radical Structure Theorem 48
Ramification,  -ramification index 13 -ramification index 13
Ramification, relative ramification index 23
Rational place 124
Real closed 4
Real closure 4
Regular extension 64
Relation, defining relation 52 112
Relative residue degree 94
Relative type 94
Residue degree 15
Riemann space 124
Ring,  — Kochen ring 102 — Kochen ring 102
Ring, Bezout ring 117
Ring, holomorphy ring 104 134
Ring, Kochen ring 135
Ring, Pr fer ring 117 fer ring 117
Rule 11
Schreier 4
Sign function 76
Spectral Structure Theorem 114
Subfield Structure of the  -adic closure 59 -adic closure 59
Substructure completeness 91
Tarski’s Transfer Principle 5
Teichm ller representative set 39 ller representative set 39
Theorem,  -adic Analog of Hilbert’s -adic Analog of Hilbert’s 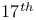 Problem 148 149 Problem 148 149
Theorem, Algebraic Embedding Theorem 53
Theorem, Characterization Theorem ( -adic) 9 -adic) 9
Theorem, Characterization Theorem (real) 4
Theorem, Elementary Equivalence Theorem 90
Theorem, Embedding Theorem for regular extensions 65
Theorem, General Embedding Theorem 63
Theorem, Isomorphism Theorem for  -adic closures 9 -adic closures 9
Theorem, Isomorphism Theorem for algebraic extensions 57
Theorem, Isomorphism Theorem for real closures 4
Theorem, Model Completeness Theorem 86
Theorem, Nullstellensatz 143
Theorem, Place Existence Theorem 125
Theorem, Principal Ideal Theorem 118
Theorem, Quantifier Elimination Theorem 91
Theorem, Radical Structure Theorem 48
Theorem, Subfield Structure of  -adic closure 59 -adic closure 59
Totally positive 3
Transfer principle,  -adic 10 -adic 10
Transfer principle, Tarski’s 5
Type (e,f) 92 93
Ultra-filter 18
Ultra-power 17
Uniqueness of  -adic closure 37 -adic closure 37
Unit, level of a unit 45
Universal axiom 83
Valuation,  -valuation 7 -valuation 7
Valuation,  -valuation of type (e,f) 93 -valuation of type (e,f) 93
Zariski topology 124
Zariski-dense 145
Zariski’s Local Uniformization 142
Zero support 18
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -adic Analog of Hilbert’s
-adic Analog of Hilbert’s 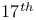 Problem
Problem  — Kochen ring
— Kochen ring  -saturated
-saturated  -group
-group  -adic Kochen operator
-adic Kochen operator 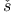 ov
ov  fer ring
fer ring